量子 ─ 黑體輻射
定義
我們知道一個熱物體會發出輻射(電磁波),這個輻射來自於電子加速和分子的振盪(古典上的)。
Thermal radiation is electromagnetic radiation emitted by the thermal motion of particles in matter. All matter with a temperature greater than absolute zero emits thermal radiation. The emission of energy arises from a combination of electronic, molecular, and lattice oscillations in a material.
所以有熱度的物體都會發光,只是看你多熱,發出的光有沒有在你可見光的頻譜內(我們看到的火爐紅色的)。
那麼假想現在在一個空間,如果某一個物體和環境達到熱平衡,公式描述
\[入射(環境給物體) = 物體反射 + 物體本身自己溫度的發射\]物體反射多少和自己發射多少就看是什麼材質的,但反正因為熱平衡,總和一定要等於入射的,這樣物體的溫度才不會再有變化(熱平衡)。
那如果我們在一個達到熱平衡的環境中看物體的話,其實什麼都看不到,因為我們能看到的就是物體 反射 + 本身發射的結果,但那又等於空間中的輻射,就代表整體都一樣了!
已達到熱平衡的環境中,空間中的輻射和周遭有什麼物體沒有關係,就是看到一片亮光,看不到放了什麼東西
我們可稱這個空間中的輻射叫做 空腔輻射 或是 黑體輻射。
黑體是什麼意思呢?整理一下
\[空腔輻射 = 入射 = 反射 + 本身發射\]如果 反射 = 0,代表全吸收
那麼
\[空腔輻射 = 本身發射\]的物體就我們就稱為理想黑體。
而因為這個空腔輻射在各個方向都會是一樣的,任何一個物體只要屬於理想黑體,就跟他是什麼物質沒關係,只要反射=0就行。
這樣的普適性小結得
\[空腔輻射 = 黑體輻射\]黑體輻射的特性和物體毫無關係,而且透過空腔輻射來研究就好。
我們通常畫的圖,一個空腔開個小洞就是想要表達這個意思,進來的輻射不太可能出去(都吸收了),但這個小洞還是會偶爾跑出一些輻射,所以黑體輻射其實就是指這個洞放出的輻射(燒營火的黑體輻射也是指中間的洞),然後跟這個洞的材質是啥無關。而我們想要從黑體輻射中看到的,想從這個洞看到的,就是這顆球裡面到底發生什麼事情,裡面的電磁波在熱平衡的時候是什麼樣子的。
空腔中的電磁波就是由腔壁之帶電粒子振動而發出。
輻射的波長分布
黑體輻射波長分布大概長這樣子,可以看到不同溫度最高峰的地方不一樣,通常越高溫,波峰會往短波長(頻率高)移動
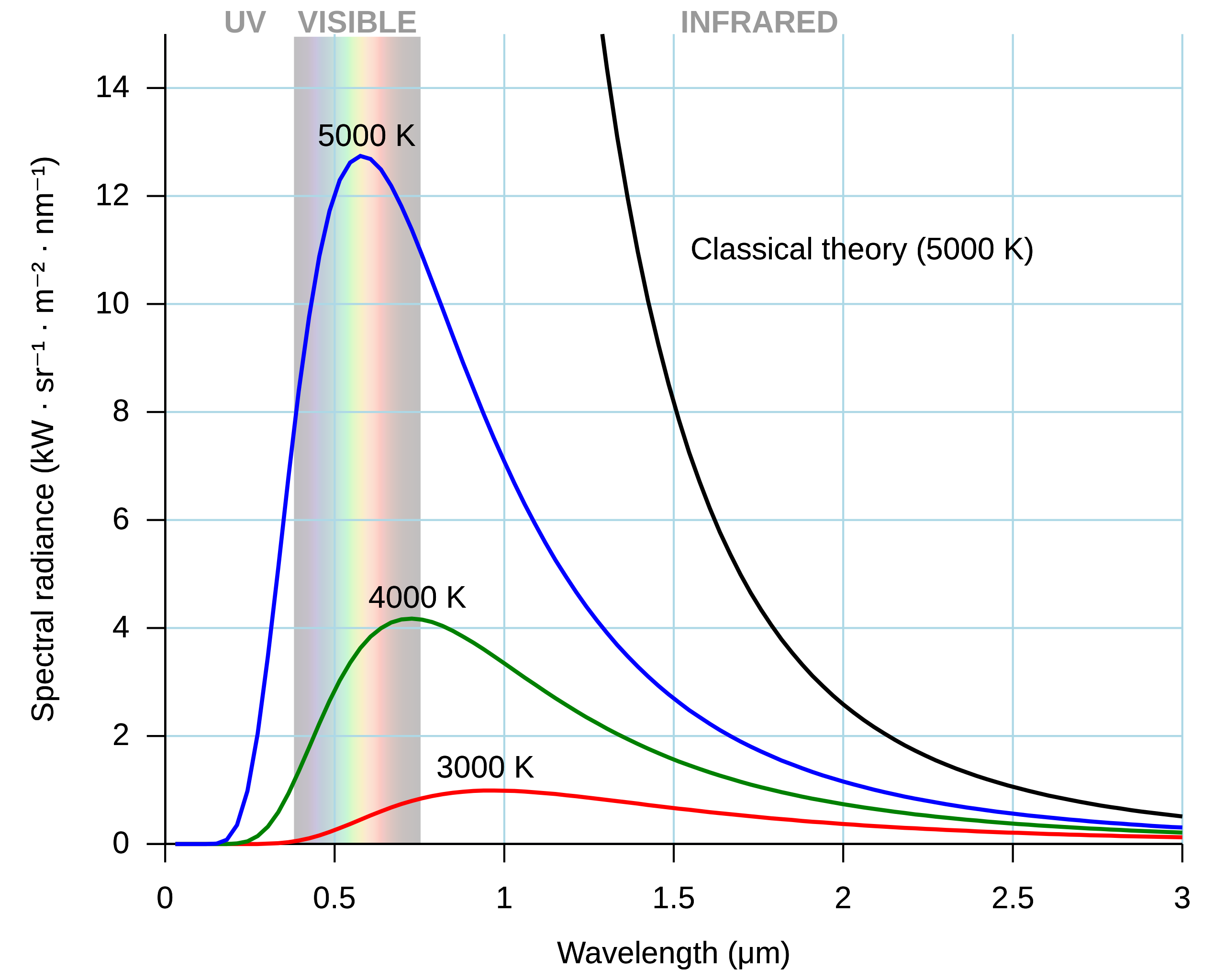
要描述這個波形,一開始可以用兩條公式描述
- Wien’s Radiation Law: \(\mu_\lambda(T)=A\lambda^{-5}e^{-B/ \lambda T}\)
- Rayleigh-Jeans Law: \(\mu_\lambda(T)=CT\lambda^{-4}\)
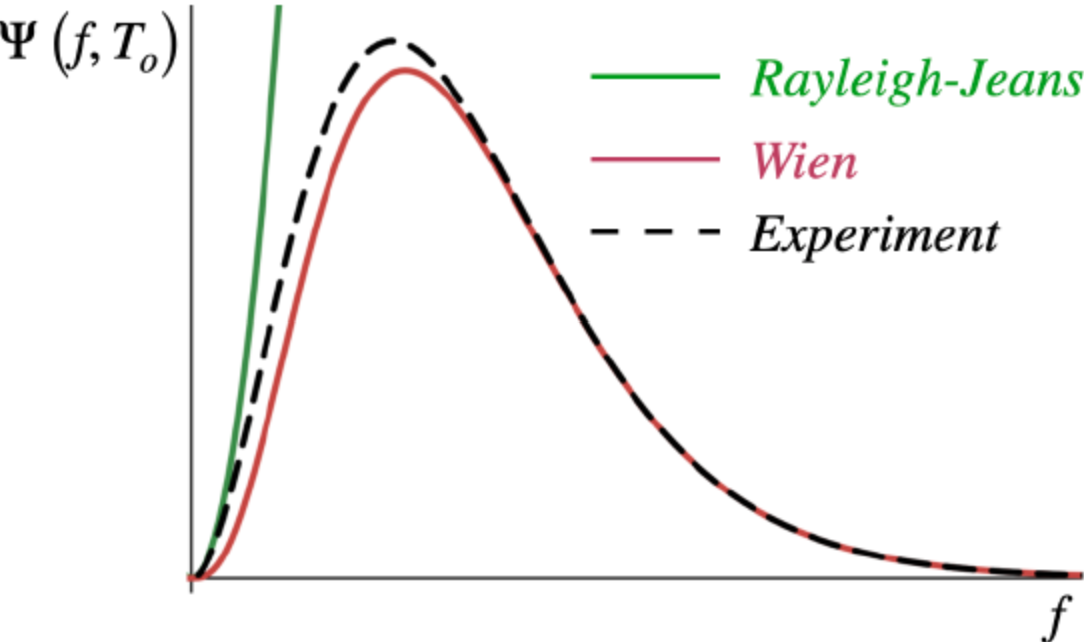
Image link(上網找的圖,橫軸是頻率)
可以看見Wien的在短波長(高頻)比較符合,Rayleigh-Jeans則是在長波長(低頻)較符合。
普朗克遇到的古典難題
普朗克,主要研究熱力學的物理學家,對於這個黑體輻射的實驗也很有興趣。
我們已知的事情是,一個系統的熵熱平衡的時候熵會達到最大值,而黑體輻射(the radiating oscillators in the walls of a cavity)的情況也是達到了熱平衡,所以普朗克加入了熵的條件之後,得到著名的Planck’s Radiation Law
\[\mu_\lambda=\frac{8\pi hc \lambda ^{-5}}{e^{hc/ \lambda kT}-1}\]可以看到在短波長和長波長的近似下,各自會回到Wien’s Law和Rayleigh-Jeans Law,漂亮地解決了這個問題!
然而當普朗克在過程中想用統計力學驗證熵的意義時,其實碰到了古典上的問題。
從熱力學我們知道,熵在統計上可以用來計算一個系統的不確定性(機率),而普朗克想要利用波茲曼(Boltzmann)的統計方法來計算熵(計算有多少種分配方式),所以就是想知道會有多少種”能量”可能性,也就是這個振子系統的總能量能夠有多少種分配方式,結果古典計算發現有無限多種,加總起來就爆掉了!
In statistical mechanics and mathematics, a Boltzmann distribution is a probability distribution or probability measure that gives the probability that a system will be in a certain state as a function of that state’s energy and the temperature of the system.
Maxwell vs Boltzmann
這涉及到電磁波和統計熱力學的不確定性,所以勢必要探討Maxwell和Boltzmann的關係。
我們來算一下,現在給定wave number $k,\omega$已知,電磁波能量
\[E(\omega)=\left<\frac{1}{2} ϵ_0 E^2+\frac{1}{2μ_0} B^2\right>V\\ \text{V: cavity of volume}\]觀察這個形式,很像是SHO,根據之前統計力學,電磁波在熱平衡下的能量是
\[U(\omega)=kT\]According to statistical mechanics, the average energy of a SHO in thermal equilibrium is kT, independent of other detail parameters. This is known as Equipartition Theorem. And EM wave is similar to SHO, when in thermal equilibrium, equipartition theorem said energy is 1/2 kT+1/2 kT=kT
所以當Maxwell 和 Boltzmann 結合後,對於任何電磁波在任何頻率(無論頻率多高),單頻波平均能量出來就是\(kT。\)
接著簡單統計這個體積下的所有能量,把所有的\(\omega\)平均能量都加在一起!
\[U=\sum_k^\infty U(\omega)=\text{(# of EM waves)}kT\]發現電磁波加總出來爆掉了!變成無限大了啊!
一定有哪裡錯了!
電磁波?光子?
這裡先偷偷引入光子的概念,問題就出在我們不能去算熱平衡下的電磁波,要算的是熱平衡下的光子!
每個特定的$k$就是特定的光子。我們說光子一顆一顆,是指振幅是不連續的,但$k$和\(\omega\)還是連續的。而傳統古典說的連續也是指$k$,\(\omega\)和振幅都是連續的。
來看波茲曼分布,某個能量出現的機率
\[P(E)\propto e^{\frac{−E}{kT}}\]$n$份特定頻率光子的能量
\[E_n=n\hbar\omega\]普朗克當時還沒有光子的概念,但有了能量以頻率作為一份單位的猜想,然後普朗克的$n$只是想先算這樣的能量會有幾份,以及該頻率下所有可能的能量機率分布。也就是說普朗克只是把空腔壁上振子交換能量時量子化,而且只是一種數學工具而已。
所以光子達到熱平衡的時候,看到的機率
\[P_n=Ce^{\frac{-n\hbar\omega}{kT}}=Ce^{-nz}\\ z = \frac{\hbar\omega}{kT}=\text{dimensionless frequency}\]又
\[\sum_{n=0}^\infty e^{−nz}=1+e^{−z}+\cdots=1/(1−e^{−z})\]且機率總和為1
\[\sum_{n=0}^\infty P_n=1\]得出
\[C=(1−e^{−z})\]推導出
\[P_n=(1−e^{−z}) e^{−nz}\](可以看到公式顯示沒有光子的機率最大,再來是exponentially decay)
回頭算光子熱平衡的平均能量
\[\because \sum_{n=0}^\infty e^{−nz}=\frac{1}{(1−e^{−z})}, \quad\sum_{n=0}^\infty ne^{−nz}=\frac{e^{−z}}{(1−e^{−z} )^2}\] \[\begin{align} \Rightarrow U(\omega)&=\sum_{n=0}^\infty P_n\cdot(n\hbar\omega)\\ &=\sum_{n=0}^\infty (1-e^{-z})\cdot e^{-nz}\cdot nz \cdot kT \\ &= (kT)z(1-e^{-z})\sum_{n=0}^{\infty}ne^{-nz} \end{align}\]得
\[u(z)≡\frac{U(\omega)}{kT}=z(1−e^{−z})\frac{e^{−z}}{(1−e^{−z})^2}=\frac{z}{(e^z−1)}\]就是前面的普朗克公式了。
能量量子化
普朗克公式可以看到特定頻率的光子達到熱平衡的時候,如果用原本古典(電磁波振幅是連續的話),\(U(\omega)=kT, u(z)=1\),才造成全部累加之後無限多次之後爆掉。
但現在就不會爆掉了!且只有在z很小的時候才會有很大的能量,z很大的時候(高頻率)會很小,趨近於零,所以總和起來就會收斂了!
並且有一個cut off的溫度頻率,只有在這個以下的頻率才會蓬勃發展。
\[z=\frac{\hbar\omega}{kT}\\ z=1, kT=\hbar\omega \Rightarrow \omega = \frac{kT}{\hbar}\]所以普朗克在這裡引入的概念就是
- 在計算總能量的時候,不同頻率的光計算的能量以該頻率當作一個單位
- 不知道有多少個,但用整數倍的方式去計算這個頻率造成的能量機率分布(所以n積0到無限大且是整數倍),發現越高頻的機率越小(exponential decay),並引入了能量量子化的概念。
- 最後再把所有頻率的這些能量相加成總能量可以收斂。
小結
- 振動子的振動能量具有門檻值\(\hbar\omega\),就是有能量量子化的現象。
- 門檻值會隨著頻率增大而增大
- 升高溫度才容易跨過門檻。
統計補充
問:假設我有四枚硬幣,重複丟很多次,平均會出現幾次正面?
全部條列
四枚硬幣,共有$2^4=16種狀態$
| 狀態 | 正面數 |
|---|---|
| HHHH | 4 |
| HHHT | 3 |
| HHTH | 3 |
| HTHH | 3 |
| THHH | 3 |
| HHTT | 2 |
| HTHT | 2 |
| HTTH | 2 |
| TTHH | 2 |
| THTH | 2 |
| THHT | 2 |
| HTTT | 1 |
| THTT | 1 |
| TTHT | 1 |
| TTTH | 1 |
| TTTT | 0 |
每一個狀態機率(硬幣公平)
\[P=\frac{1}{2}\times \frac{1}{2}\times \frac{1}{2}\times \frac{1}{2} = \frac{1}{16}\]平均正面數
\[\langle N_H \rangle = \sum_{\text{states}} P(\text{state}) \times (\text{正面數})\]把剛列的表加起來
\[\langle N_H \rangle\\ = \frac{1}{16}(4 + 4\times3 + 6\times2 + 4\times1 + 0)\\ = \frac{32}{16}\\ = 2\]答案:平均 2 個正面。
叫做Ensemble average。
計算平均值
對單一硬幣:
- 正面機率 = 1/2
- 反面機率 = 1/2
定義隨機變數:
\[X_i = \begin{cases} 1 & \text{正面}\\ 0 & \text{反面} \end{cases}\]所以單一硬幣期望值
\[\langle X_i \rangle = 1\times\frac{1}{2} + 0\times\frac{1}{2} = \frac{1}{2}\]把四枚硬幣加起來
總正面數:
\[N_H = X_1 + X_2 + X_3 + X_4\\ \langle X_1 + X_2 + X_3 + X_4 \rangle = \langle X_1\rangle + \langle X_2\rangle + \langle X_3\rangle + \langle X_4\rangle\\ \langle N_H \rangle = 4 \times \frac{1}{2} = 2\]答案也是 2。
所以換到普朗克在做的事情,跟硬幣稍微類比一下
- 一枚硬幣 = 一個振子(頻率)
- 正反可能性 = 能量包 (1hf, 2hf, 3hf,…nhf)
- 每面機率 = 波茲曼分布
- 列舉所有組合 = 列舉所有振子各自不同nhf的組合 (譬如第一組合振子1 = 2hf1, 振子2 = 1hf2…第二組合 振子1 = 3hf1, 振子2 = 2hf2)
- 平均正面數 = 平均能量
普朗克就是在已知的平均總能量下(平均正面數 = 2),去算各個頻率(每個硬幣)可能出現的n個能量包(正反兩面)狀態,列舉的話就是組合起來每個頻率可能是多少能量的情況下(列舉所有HHLH等),平均的話就是直接算該頻率積分n從0到無限大平均是多少(每個硬幣出現的期望平均),能達到總和。
因此每個頻率自己算一次(積分n),最後總和每個頻率會再算一次。
