(9) 熱力 ─ 資訊熵 with Shannon Entropy
前面說到系統一旦DOF或是data太大就會很難算,需要引入統計的概念。
現在我們先跳脫出熱力學的框架,來看一個簡單的系統,我們會了解到,熵的概念不只是在熱力學,更是整個世界資訊的一種不確定的描述方式。
Bernoulli Distribution
來看最簡單的統計系統,一個銅板,你亂丟不是正面就是反面,更專業的名字為Bernoulli Distribution。
我們關注的問題就是丟完之後是哪一面,所以定變數(Random Variable)
\[X=0, 1\]0為反面、1為正面。
接著描述丟出來是正面和反面的機率
\[P(X)=\begin{cases} P, \quad X=1\\ 1-P, \quad X=0 \end{cases}\]注意$X$不是連續的,也沒有極限,所以無法算微積分。
但是機率函數$P(X)$是連續的,可作微積分,譬如說是公正的銅板,那機率永遠是1/2,也是個常數函數可以做微積分。
然後我們知道期望值定義
\[\langle X^n \rangle=\sum_X X^n P(X)\]所以Bernoulli
\[\langle X\rangle=P\cdot 1+(1-P)\cdot 0=P\]標準差
接者定義很重要的指標,標準差!
\[\Delta X\equiv \sqrt{\langle X^2\rangle-\langle X\rangle^2}=\sqrt{P-P^2}=\sqrt{P(1-P)}\]$\Delta X$ is a good index for fluctuations from its average.
譬如說$\Delta X=0$的情況,就像一個班級平均60分來自於每個人都考60分,代表只有一種可能性,是確定性的。
以銅板例子來看,$\Delta X=0$代表著$P=1$(都只出現正面)或是$P=0$(都只出現反面),都是確定性的。
所以要記得只有當$\Delta X\neq 0$,才會有不確定性的存在!標準差要給出來才代表有統計意義和指標!
連續 Random Variable
這邊稍微進一步延伸一下,前面銅板例子的random variable是discrete的,非0即1,但如果是連續的,那我們就要用積分的方式寫
\[\int p(x)dx=1\]其中$p(x)$就不是機率了,是機率分布!(有因次,random variable導數)
所以
\[\langle x^n \rangle=\int dx p(x) x^n\] \[\langle x\rangle=\int dx p(x) x\] \[\Delta x\equiv\sqrt{\langle x^2\rangle-\langle x\rangle^2}\]在連續的情況下,我們會說$p(x)dx$才是機率,並且是random variable落在$(x, x+dx)$的機率。
注意這裡是有區間的,假設一條線[0,1],隨便丟個球,落在[0,0.3]的機率是0.3,落在[0,0.8]的機率是0.8。若你只是說球剛好落在0.2的機率、剛好落在0.6的機率,那都是0,只有區間算機率才有意義。
(當然這有點奇妙,你每一點都是零,但你積分全部機率就會是1 XD)
Dog Flea Model
那我們繼續回到最前面的問題,如何量化不確定性。
這裡用一個簡單的toy 模型,Dog Flea Model,就是蝨子會在兩隻狗上面跳來跳去,我們要隨時看他會在哪隻狗的頭上。
那我們開始來算吧!(簡化一點假設是discrete的)
- 第一隻狗設$X=0$,第二隻狗設$X=1$。
- $P(t)$代表時間$t$找到蝨子在$X=1$的機率。
- random variable t 為時間且discrete \(t=0,1,2,3,4,\cdots\quad\quad \Delta t = 1\)
- 蝨子有$\frac{1}{\tau}$的機率會跳到另外一隻狗上
- 初始條件蝨子在第一隻狗($X=0$)頭上 $P(0)=0$。
所以時間$t+1$時在$X=1$的機率,等於上一秒在$X=1$但不跳,加上在$X=0$並跳的機率:
這個就是Master Equation。
達到平衡的機率
在平衡時,那機率應該都是一樣的
\[P(t+1) = P(t)=P_\infty\]所以代回去剛剛的Master Equation
\[P_\infty = P_\infty\left(1-\frac{1}{\tau}\right)+(1-P_\infty)\frac{1}{\tau}\\ =P_\infty - \frac{1}{\tau}P_\infty+\frac{1}{\tau}-\frac{1}{\tau}P_\infty\\ \frac{1}{\tau}(1-2P_\infty)=0\Rightarrow P_\infty = \frac{1}{2} \quad(\tau \neq 0)\]$P_\infty=\frac{1}{2}$代表最後達到就是熱平衡,也就是我們無知的狀態(機率一半一半根本不知道蝨子在哪了)。
機率演化公式
所以現在我們知道
- $P(0)=0$
- $P_\infty=\frac{1}{2}$
那中間任一時刻的機率呢?機率又是怎麼從0演化成$\frac{1}{2}$的?
這時我們可以用一個代數來輔助解釋,定
\[Q(t)\equiv P(t)-P_\infty=P(t) - \frac{1}{2}\\ \therefore Q(t+1)+\frac{1}{2}=P(t+1),\quad Q(t)+\frac{1}{2}=P(t)\]代回Master Equation
\[\begin{align*} Q(t+1)+\frac{1}{2} &=P(t+1) = P(t)\cdot\left(1-\frac{1}{\tau}\right)+\left[1-P(t)\right]\frac{1}{\tau}\\ &=\left(Q(t)+\frac{1}{2}\right)\cdot\left(1-\frac{1}{\tau}\right) +\left[\frac{1}{2}-Q(t)\right]\frac{1}{\tau}\\ &=Q(t)-\frac{1}{\tau}Q(t)+\frac{1}{2}-\frac{1}{2\tau}+\frac{1}{2\tau}-\frac{1}{\tau}Q(t)\\ Q(t+1) &=\left(\frac{\tau-2}{\tau}\right)Q(t)\\ Q(t) &=\left(\frac{\tau-2}{\tau}\right)Q(t-1)\\ &=\left(\frac{\tau-2}{\tau}\right)\left(\frac{\tau-2}{\tau}\right)Q(t-2)\\ &=\left(\frac{\tau-2}{\tau}\right)^tQ(0)\\ &=\left(\frac{\tau-2}{\tau}\right)^t\Bigl(P(0)-\frac{1}{2}\Bigr)\\ &=\left(\frac{\tau-2}{\tau}\right)^t\Bigl(0-\frac{1}{2}\Bigr)\\ &=-\frac{1}{2}\left(\frac{\tau-2}{\tau}\right)^t \end{align*}\]最後得到
\[P(t)=Q(t)+\frac{1}{2}\\ \Rightarrow P(t)=\frac{1}{2}-\frac{1}{2}\left(\frac{\tau-2}{\tau}\right)^t\]就是機率隨時間演化的公式了。
從這裡可以看到,因為$\left(\frac{\tau-2}{\tau}\right) < 1$,所以起始$t=0$的時候,$P(0)=0$,$X=1$還沒有被感染,但隨著時間越來越大,第二項越來越小,代表開始被感染了,直到最後蝨子在兩顆頭一直跳來跳去,機率就是$\frac{1}{2}$。
達到平衡的時間
假設 $\tau\Delta t \gg 1$,代表大部分的時間都是沒有在動的,所以可以把$t$視為連續的,因此
\[\frac{\Delta Q}{\Delta t}=\frac{Q(t+1)-Q(t)}{1}\approx \frac{dQ}{dt}\]就可以寫成微分的樣子了。
而前面我們算到
\[Q(t+1)=\left(1-\frac{2}{\tau}\right) Q(t)\\ \Rightarrow Q(t+1)-Q(t)=\Delta Q = \frac{\Delta Q}{\Delta t}=\frac{-2}{\tau}Q(t)\]改成微分方程,我們知道最後一定是個exponential解,所以係數可以這樣定
\[\frac{dQ}{dt}=-\frac{1}{\tau_{eq}}Q\\ Q(t)=Q(0)e^{-\frac{t}{\tau_{eq}}}\]exponential那項就是代表exponential decay,relaxation時間就是$\tau_{eq}$,意思就是說經過$\tau_{eq}$時間後,原本的數值會降成$e^{-1}$倍,我們通常把這個時間當作將近達成平衡的時間。
再把兩者比對一下
\[\tau_{eq}=\frac{\tau}{2}\]代表一開始蝨子跳轉的機率,決定了這個系統多快可以達到平衡($\frac{\tau}{2}$的時間),若$\tau$越大,那麼就會更晚達到平衡(但是仍然會達到平衡),實際生活中我們可以用這個來估算傳染病會傳得多快。
最後整理一下,隨時間演化的機率就是
\[P(t)=\frac{1}{2}-\frac{1}{2}e^{-\frac{t}{\tau_{eq}}}\quad(\because Q(0)=-\frac{1}{2})\]我們能掌握機率的什麼?
這樣看下來,蝨子在兩個頭上跳來跳去,到底會是哪個頭我們是不知道的,頭本身就是一個random variable,沒有辦法被預測。
我們唯一能夠控制的,是他們背後亂跳的機率分布(也就是我們求的$P(t)$),這件事情可以被預測也可以被算出來。
所以在面對統計系統的不確定時,我們不是想要去知道每一個人他手上的硬幣到底是正面還是反面,而是想問控制全班的機率分布長什麼樣子,這個機率分布的公式能夠遵循什麼規則(Master Equation)。
Not try to find the right person. Try to make yourself a right person, so the right person will come to you. The only thing you should work on is Probability Distribution, not the random variable. If you still meet a wrong person in the end, that’s…… just what the random variable means.
Shannon Entropy
到這裡把機率都算完了,我們現在回來前言的問題:
如何界定一個統計系統的不確定性?
答案就是使用Shannon Entropy,其定義為
\[\sigma = \langle -\ln P \rangle=\Sigma_n -P_n \ln P_n\]括號就是在算機率的期望值,負號是因為通常機率<1,取$\ln$會變成負號,因此補回變成正的,而要取Log的原因是我們想要方便計算多個系統的Entropy,取Log的話就可以直接用相加的(必須是獨立系統)。
所以對於前面的Bernoulli distribution來說
\[\sigma = -P\ln P-(1-P)\ln(1-P)\\ \lim_{P\to 0^+} P\ln P = 0\\ \text{if}\quad P=\frac{1}{2}\Rightarrow \sigma = -\frac{1}{2}\ln\frac{1}{2}-\frac{1}{2}\ln\frac{1}{2}=\ln 2\]所以可以畫出機率和Entropy的圖,可以看到$P=\frac{1}{2}$的時候,Entropy是最大的,而$P=0$和$P=1$時,Entropy = 0。
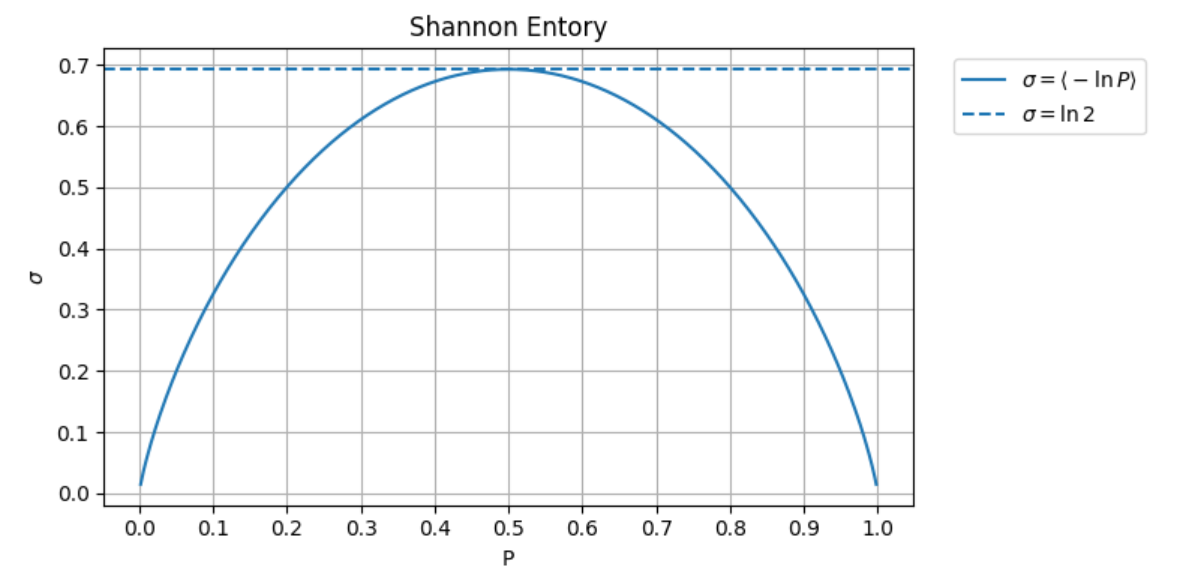
這也很合理,因為$P=0$和$P=1$是確定的,就像丟銅板,永遠都是反面或永遠都是正面,一定知道答案,這樣的機率系統就沒有凌亂程度,但如果丟的機率有一半是正面一半是反面,那這個系統的凌亂程度就會是最大的。
因此記住Shannon Entropy 就是在告訴我們以資訊的角度來看這個統計系統的凌亂程度,告訴我們這個系統有多不確定。
Information Capacity for 1 bit
題外話一下,因為現在舉的例子是Bernoulli distribution,所以這個$\ln2$的結果也可以代表我們現在電腦系統資訊儲存1 bit的 capacity。
假使現在有兩個銅板,$P=\frac{1}{4}$,那麼算出來$\sigma=2\ln 2$,亂度變為兩倍,但其實可能性變成四種。
若有三個銅板,$P=\frac{1}{8}$,算出來$\sigma=3\ln 2$,亂度變為三倍,但可能性變成八種。
亂度和實際的結果,前者是線性增加,但後者卻是exponential增長的。
隨時間演化到熱平衡
那一樣,在Bernoulli distribution的情況下,Shannon Entropy隨時間的演化就是
\[\sigma(t) = -P(t)\ln P(t)-(1-P(t))\ln(1-P(t))\]$P(t)$前面我們解過了,所以只要你知道機率分布,就會知道怎麼算Entropy,並且推出下個瞬間的機率分布。
畫個圖
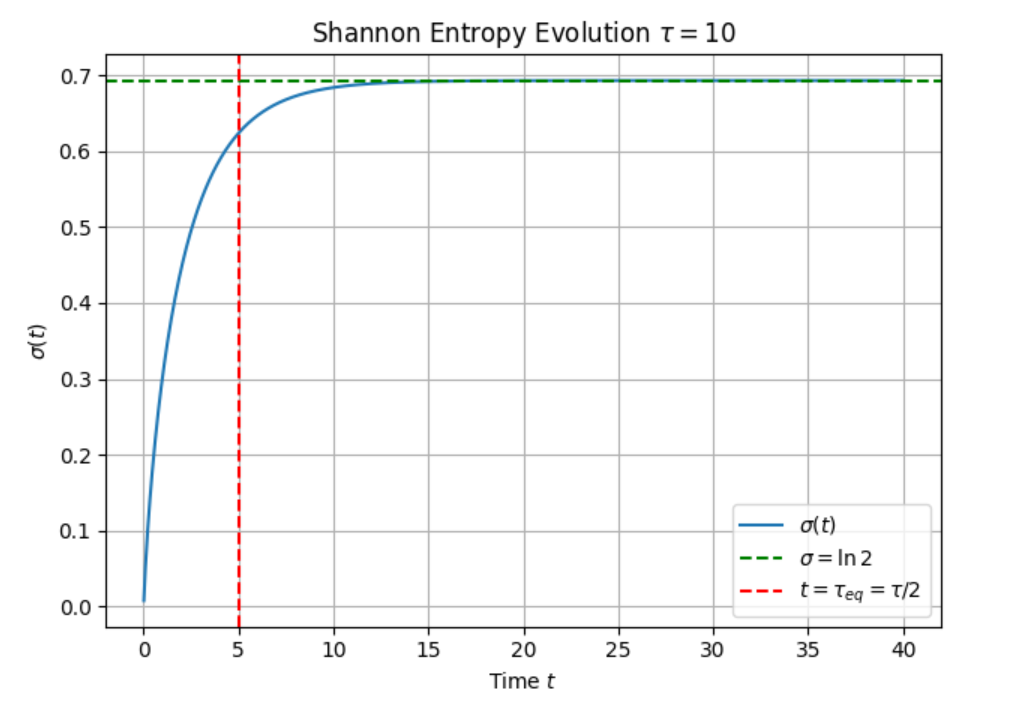
一開始亂度就是0,然後Entropy就會持續上漲(monotonically incresing)到最後最大值(熱平衡),這個其實就是熱力學第二定律。
但這是資訊角度的Entropy,跟我們前面提到的從熱出發的定義好像不太一樣,下節會把這兩者合再一起!
