(7) 熱力 ─ 熵 & 熱力學第二定律
這節開始來講熵,口說同音稱商,火字旁為取自熱力學(thermodynamic variables),商則因為其公式為 $\frac{\text{熱}}{\text{溫度}}$。
可逆 Thermal Cycle
前一章節已經介紹過循環路徑的Thermal Cycle,現在我們把內能、熱、作功積一圈來看看。
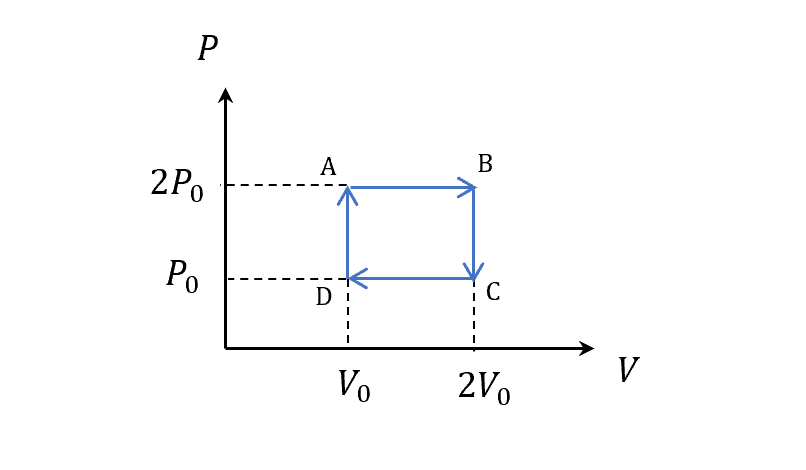
因為內能只和溫度有關,積一圈回來,同樣的PV,T也一樣,那麼圈內面積就是這個cycle的功和吸的熱
\[\Delta U = 0\\ W=Q=\text{Enclosed area}\]微分式
\[W=\oint dW \neq 0\\ Q=\oint dQ \neq 0\\ \Delta U = \oint dU = 0\rightarrow U\text{ is a state function}\]所以看cycle(引擎)的時候不是只看狀態的結果,不同的過程會不同,不同的過程才決定了引擎的好壞。
竟然熱量和功積一圈不會等於0,我們回頭來看另外一個積一圈會等於0的公式(注意這裡只有可逆時才成立,代表積一圈時,沒有能量耗散,像是不可回復的摩擦力作用在裡面。):
\[\oint \frac{dQ}{T}=0\]所以熱力學第一定律微分式可以寫成以下這樣
\[dU = dQ-PdV\\ \Rightarrow \frac{dQ}{T}=\frac{dU}{T}+\frac{P}{T}dV\]接著我們來作分段路徑積分。
等壓膨脹 $A\to B$
定個符號$S$
\[\begin{align} S_{A\to B} &\equiv \int_A^B \frac{dQ}{T}=\int_A^B \frac{dU}{T}+\frac{P}{T}dV\\ &=nC_v\int_A^B \frac{dT}{T}+nR\int_A^B \frac{dV}{V}\\ &(\because dU=nC_v dT,\quad T=\frac{PV}{nR})\\ &=nC_v\ln \left(\frac{T_B}{T_A}\right)+nR\ln\left(\frac{V_B}{V_A}\right)\\ &=n(C_v+R)\ln 2\\ &=nC_p \ln 2\\ &(\because \frac{T_B}{T_A}=\frac{4P_0 V_0}{2P_0 V_0}) \end{align}\]定容壓縮 $B\to C$
\[\begin{align} S_{B\to C} &\equiv \int_B^C \frac{dQ}{T}\\ &=nC_v\int_B^C \frac{dT}{T}\\ &=nC_v\ln \left(\frac{T_C}{T_B}\right)\\ &=nC_v\ln \frac{1}{2}\\ &=-nC_v \ln 2 \end{align}\]等壓壓縮 $C\to D$
\[\begin{align} S_{C\to D} &\equiv \int_C^D \frac{dQ}{T}\\ &=nC_v\ln \left(\frac{T_D}{T_C}\right)+nR\ln\left(\frac{V_D}{V_C}\right)\\ &=-nC_p\ln 2 \end{align}\]定容加壓 $D\to A$
\[\begin{align} S_{D\to A} &\equiv \int_D^A \frac{dQ}{T}\\ &=nC_v\int_D^A \frac{dT}{T}\\ &=nC_v\ln \left(\frac{T_A}{T_D}\right)\\ &=nC_v\ln 2 \end{align}\]總和
全部拼起來
\[\begin{align} \oint\frac{dQ}{T}&=S_{A\to B}+S_{B\to C}+S_{C\to D}+S_{D\to A}\\ &=nC_p \ln 2+(-nC_v \ln 2)+(-nC_p\ln 2)+nC_v\ln 2\\ &=0 \end{align}\]熵 - Entropy
這樣積一圈回來等於0,其實就很像是某種potential(像是以前學的保守力),這樣的狀態函數我們定為 Entropy,僅和狀態有關,和路徑無關。
\[\frac{dQ}{T} = dS\\ dQ=TdS\]Entropy is a state function.
所以任意PV圖的兩個點,我們可以計算差值,並只看端點狀態
從 $dS$ 看凌亂程度
現在我們進一步來看$dS$的特性,先分別畫出各個狀態下的氣體狀況
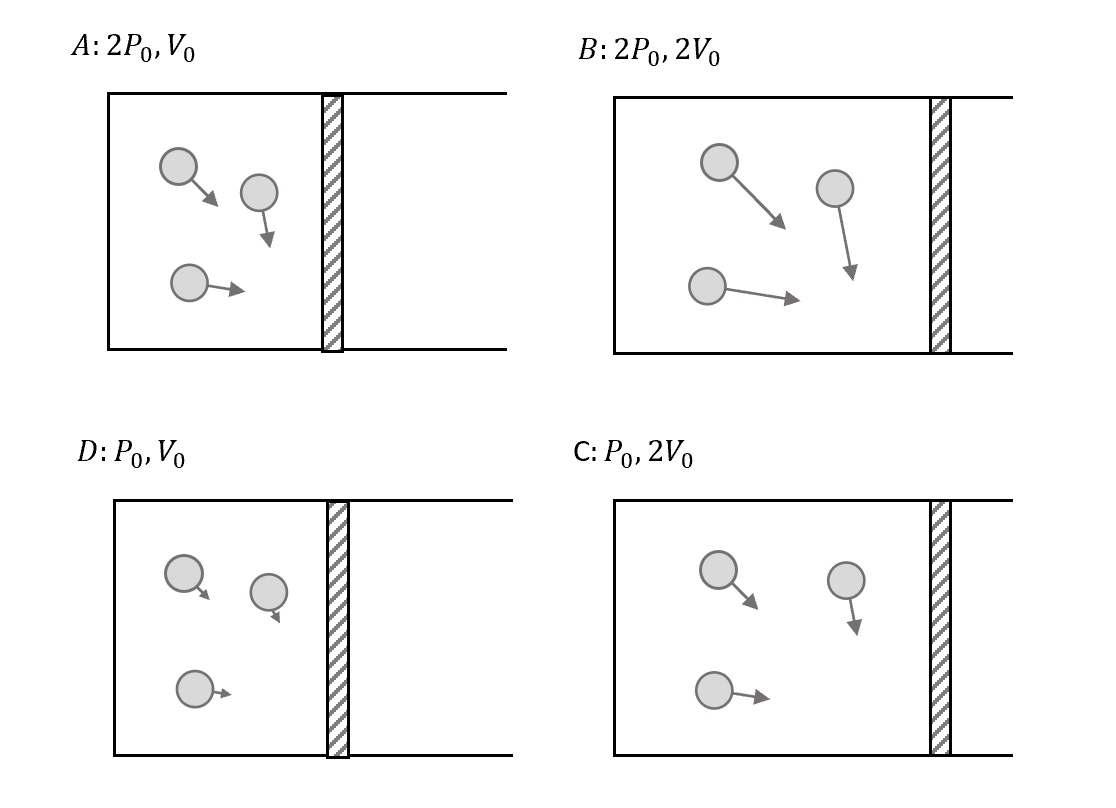
這樣就可以來對每個狀態的Entropy進行排序的關係式了!
\[S(B) > S(C) > S(A) > S(D)\]溫度的話就是PV相乘,所以
\[T(B) > T(C) = T(A) > T(D)\]那這個大小有什麼意義呢?我們可以用來判斷該系統的凌亂程度!
首先我們來看為什麼 $S(B) > S(C)$。
先看兩者的空間,都是$2V_0$,空間一樣亂,但是溫度因為B比較大,速度上B較亂,所以整體的$S(B)$就會比較亂。
同理來看 $S(C) > S(A)$,雖然溫度一樣,所以速度一樣亂,可是C可以亂的空間比較大,所以整體的$S(C)$就更亂。
其他$A,D$和$B,C$也同理。
所以在統計力學上面,可以把 Entropy S 和 “the degrees of disorder” 的概念連結在一起,去定量的描述這個系統的亂的程度。
古典小結邏輯:畫PV圖,發現大部分物理量積一圈幾乎都不是零,但是把$dQ/T$去積一圈卻是零,告訴我們可以定義像位能一樣的東西,就是Entropy,定義出來之後,我們用常識把Entropy把不同狀態做比較,產生了概念,定義出來的Entropy似乎跟系統的凌亂程度有關係。
熱力學第二定律
不過到現在為止,感覺一切都莫名其妙對吧?
前面路徑、數學計算雖然看起來合理,但是怎麼突然就定義了一個特別的熵的數學量,然後套用氣體模型,又說這個跟系統的凌亂程度有關係。
對,這的確都很莫名其妙。
但在這之前,我們還是要付諸於對生活的直覺。
熱力學第一定律告訴我們的只是能量守恆,任何一種過程(process)都能夠符合。
但是現實生活中,我們知道並不是所有過程都會發生,即便他跟能量守恆沒有衝突,譬如說
- 冰塊放進水里不會讓水的溫度上升
- 熱永遠高溫流向低溫,不會低溫流向高溫
- 在水裡溶解的可可粉,不會再攪一攪又收回成一坨
這樣的一種自然常識理解,其實反應著自然過程是有「方向性」的。
這個方向性,就是熱力學第二定律,這個定律解釋了
- 高溫流向低溫
- 熱機效率
- 化學平衡
- 資訊傳遞
- 自然演化方向性
也和前面說到的熵有關係。
熵的視角 - 完美冷機
複習一下前一章節說的完美冷機
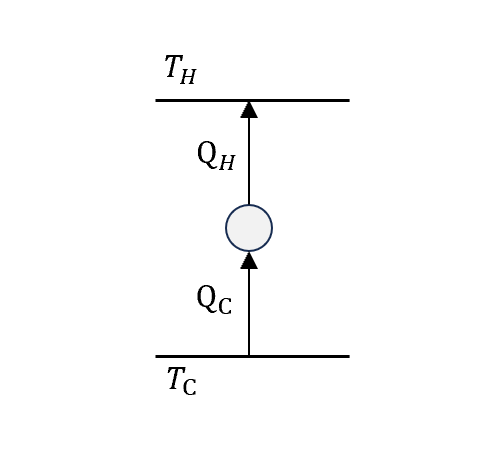
我們切成三段帶入熵的公式
- 第一項:對高溫庫來說,熱流入,正號
- 第二項:對低溫庫來說,熱流出,負號
- 第三項:對cycle engine來說,state回到原本,熵不變
換算一下,總系統(熱庫+engine)的熵變化
\[\Delta S=Q\left(\frac{1}{T_H}-\frac{1}{T_C}\right)<0\]可是!!因為完美冷機不可能存在(前面證明),所以\(\Delta S<0\)是不可能的。
更正式的描述是,當完成一個cycle,系統的熵變化一定要是
\[\Delta S \ge 0\]這就是熱力學第二定律和熵的關係,
熱力學第二定律告訴我們沒有完美冷機的存在,代表熱只能從高溫流向低溫,從高溫流向低溫這件事情本身就是會讓Entropy上升。
熱力學第二定律、高溫流向低溫、熵會增加都是指同一件事。
熵的視角 - 高溫流向低溫
接著讓我們來看一般的熱庫系統,沒有heat engine
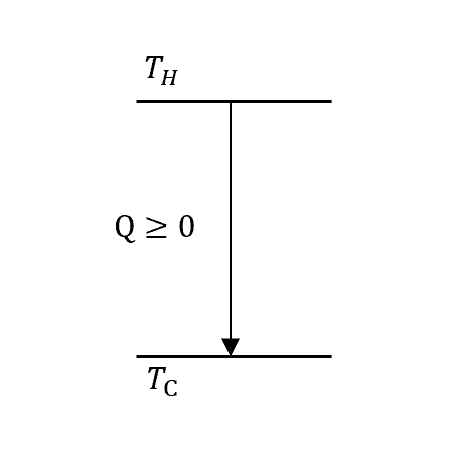
熱力學第一定律得
\[-Q+Q=0\]第二定律
\[\Delta S = -\frac{Q}{T_H}+\frac{Q}{T_C}=Q\left(\frac{1}{T_C}-\frac{1}{T_H}\right)\ge 0\]看Entropy的時候,高溫的Entropy\(-\frac{Q}{T_H}\)是下降的,低溫的Entropy\(\frac{Q}{T_C}\)是上升的,算出來的總和是增加的!
所以真正的第二運動定律不是說所有東西會一直變亂,就像假設你家有十個房間,你整理一間房間讓Entropy下降,勢必會創造你以外的房間的Entropy上升,但對整個家來說,總體的Entropy是上升的。
對於一個獨立的系統來說,若可逆,則$\Delta S = 0$,若不可逆,則$\Delta S > 0$。
因此,這麼自然的這張圖,熱流都會從高溫系統$T_H$流向低溫系統$T_C$
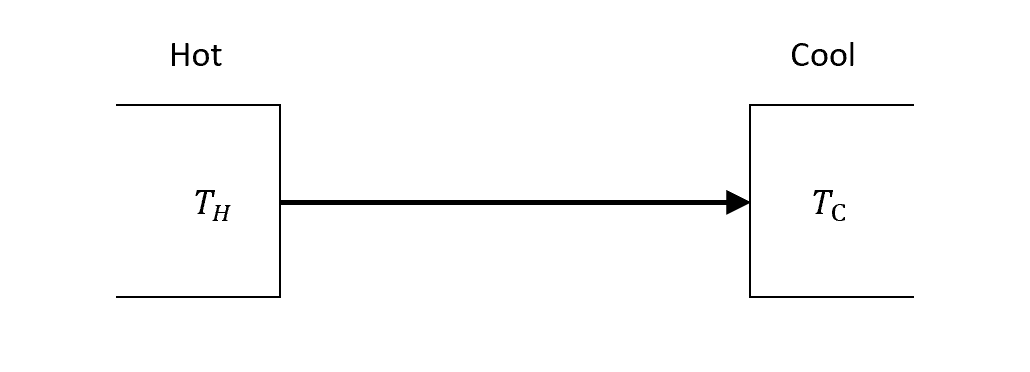
要再強調一次,即便低溫流向高溫沒有違反能量守恆,但是第二定律告訴我們,自然就只會有高溫流向低溫的方向,不能從低溫流向高溫。
所以熱力學第一定律從能量守恆來看只告訴我們熱也是能量的一部份,但並沒有告訴我們中間的dynamic發生了什麼,是熱力學第二定律才描述了這個具有方向性的過程。
熵的視角 - 卡諾循環
我們前面知道卡諾循環是
\[\frac{Q_H}{T_H}+\frac{Q_C}{T_C}=0\]現在想像如下的任意可逆的封閉循環(黃色),我們可以切成很多小卡諾循環,每一個循環都是等溫線和絕熱線組成的
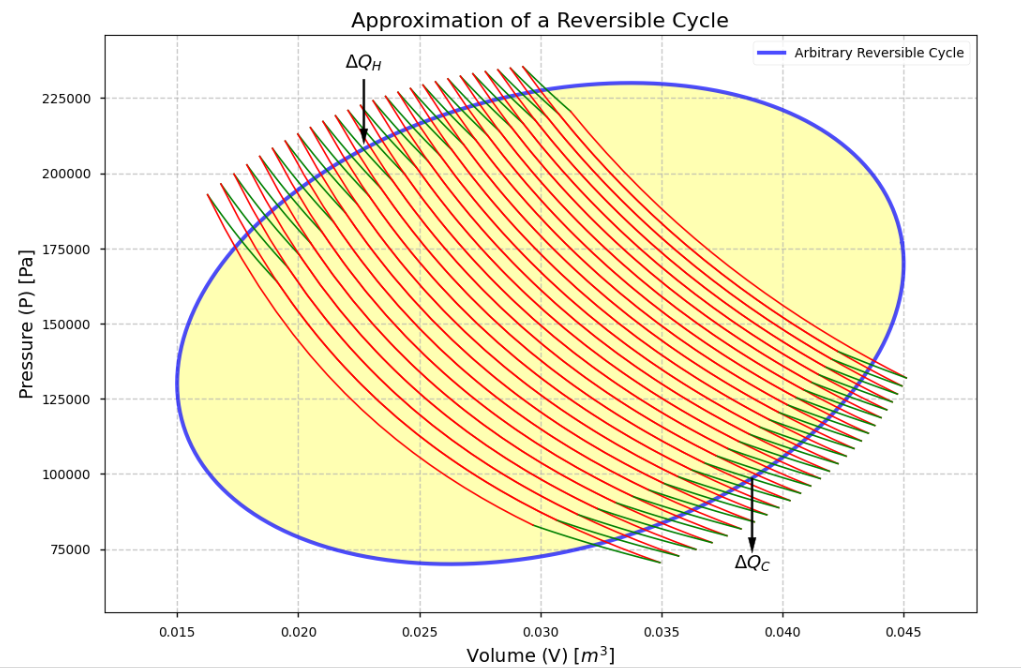
所以每一個循環都滿足
\[\frac{\Delta Q_H}{T_H}+\frac{\Delta Q_C}{T_C}=0\]全部加起來
\[\Sigma \frac{\Delta Q}{T}=0\\ \oint \frac{dQ_R}{T}=0\quad\quad(reversible)\]繞一圈回來等於零的概念,很像我們以前守恆力作功的感覺,只跟兩點狀態有關,跟路徑無關。
所以我們也定了一個狀態函數(Entropy)來描述,注意這裡的Heat一定要是可逆路徑下的
\[dS=\frac{dQ_R}{T}\]所以兩點之間的Entropy變化就是
\[\Delta S = S_f-S_i = \int^f_i \frac{dQ_R}{T}\]The change in entropy depends only on the initial and final equilibrium states, not on the thermodynamic path.
但前面我們都提到是可逆的過程,如果我們要找不可逆的Entopry變化,我們可以在不可逆過程中找到一樣的起始和終止的平衡態,然後套用可逆的路徑去計算(反正Entropy就是一個狀態函數)。
熵的視角 - 理想氣體可逆過程
\[\Delta S = nC_v\ln \left(\frac{T_f}{T_i}\right) + nR \ln \left(\frac{V_f}{V_i}\right)\]因為Entropy只和起始和終點狀態有關,所以這個也可以套用到不可逆過程(只要兩端狀態一樣)
熵的視角 - 絕熱膨脹不可逆
一旦戳破膜,氣體會快速膨脹,這時的壓力、體積和溫度沒有唯一定義,所以是不可逆的。
但因為絕熱,所以$\Delta Q =0$
然後之前有說過,對理想氣體
\[\Delta U = 0\\ \Delta T = 0\]所以套用前面熵公式
\[\Delta S = nR \ln \frac{V_f}{V_i} > 0\]那對外界來說,因為絕熱沒有熱交換,所以外界環境的熵沒有變化。
那麼整體來看,系統和外界的熵總和
\[\Delta S_{universe} = \Delta S_{gas} + \Delta S_{env} > 0\]都會大於零。
\[\Delta S \ge 0\]The change in entropy for any process, including an irreversible one, between given initial and final equilibrium states, is the same.
The entropy change in an isolated system is either zero (for a reversible process) or greater than zero (for a real, irreversible process).
基本上現實生活中都是不可逆的,所以全宇宙的熵會一直上升,即便有局部的地方變小,一定會造成其他地方變高。
In a reversible processs the entropy of an isolated system stays constant; in an irriversible process the entropy increases.
熵的視角 - 氣體軌跡
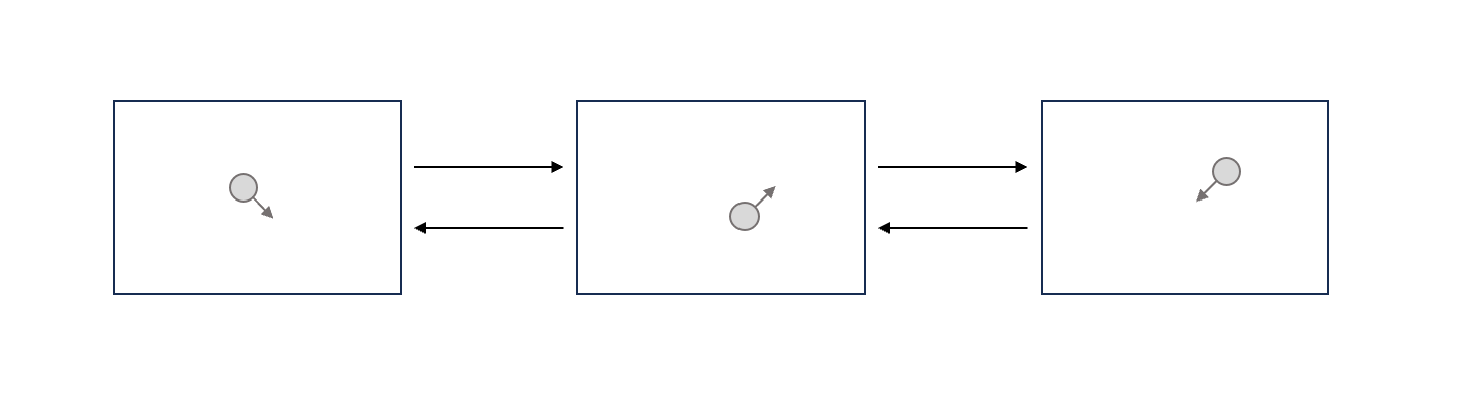
若一個容器裡面只裝一個氣體分子,氣體分子在裡面亂撞,我們紀錄移動軌跡,從第一張到第三張。
接著若倒著播放,從第三張返回到第一張,也會覺得很正常,沒有人知道你倒著放。
這是因為牛頓力學,加速度是時間的平方,所以運動方程本來就有時間逆著的對稱性。
\[\vec{F}=m\vec{a}=m\frac{d^2\vec{r}}{dt^2}\\ t\leftrightarrow -t\]可是,當我們有很多個氣體分子
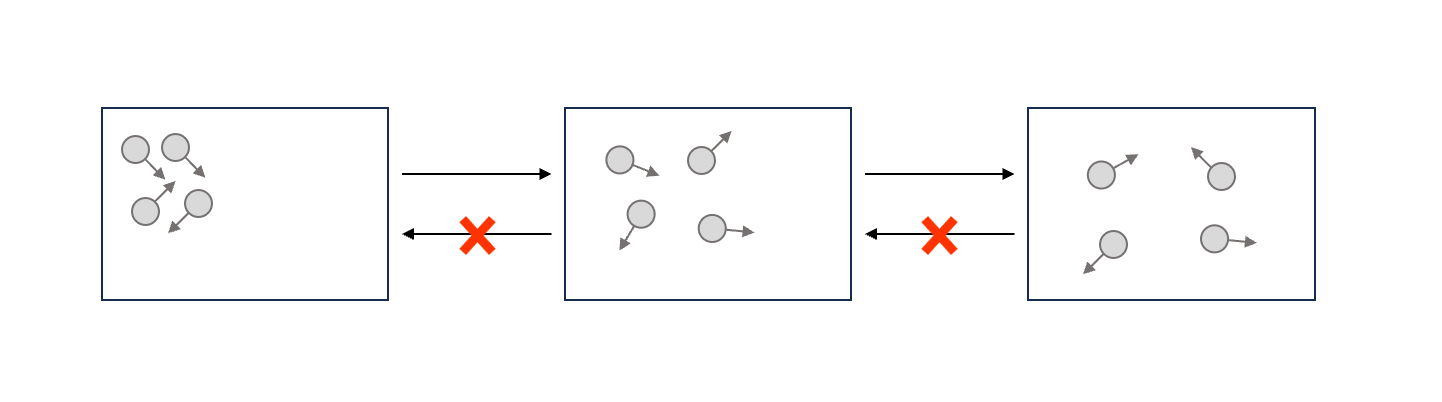
當氣體分子們開始擴散開來之後,若倒著放,你就會有感受了,所以逆過來是不會發生的。
舉個簡單生活例子,平常泡可可,把可可粉丟進水裡面泡開之後,不可能攪一攪這些可可粉還會回來聚集成一坨。
這也是另外一種熱力學第二定律的描述,或許你會懷疑,為什麼前面的運動方程在這個情況下不適用了?在多氣體分子裡面,每一個氣體分子彼此之間怎麼撞都還是可以倒著放的,為什麼一多就不行了呢?那麼要到多多才是多?這個我們之後會再繼續提。
