(5) 熱力 ─ 路徑 & 比熱
在理解了熱力學第一定律後,我們可以透過PV圖在深入了解內能、熱、功在不同路徑和條件下的變化,這樣對我們接下來引擎的理解有更多的幫助。
(一樣都假設是理想氣體)
單方向路徑
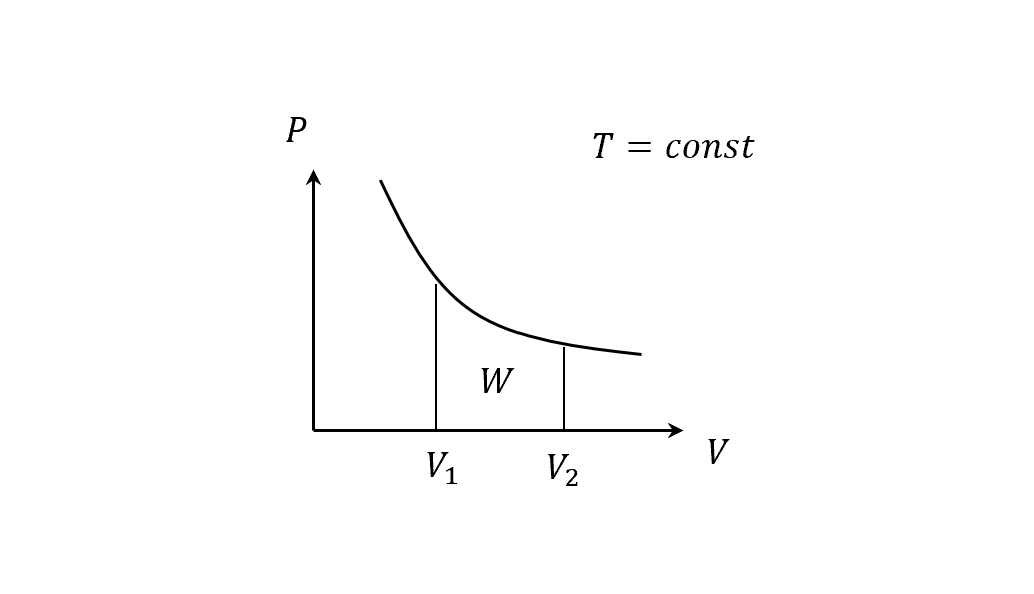
(路徑不同,底下做的功就不同)
等壓:系統膨脹或壓縮都在相同壓力
\[W = P(V_f - V_i)\]等溫:系統和熱庫接觸,維持在固定溫度
因為等溫,PV為定值,所以計算作功
\[W=nRT\int^{V_f}_{V_i} \frac{dV}{V}=nRT \ln \left(\frac{V_f}{V_i}\right)\]定容:體積不變
系統體積不變,所以作功
\[W=0\\ \Delta U = Q\]絕熱:系統跟外界沒有熱交換
沒有熱交換,譬如放在thermal insulated container,或是這個過程太快速以至於沒有足夠的反應時間進行熱交換(rapid compression stroke in the diesel engine)
\[Q = 0\\ \Delta U = -W\]這個條件下,氣體膨脹就會讓溫度下降,相反就是溫度上升。
孤立:系統跟外界沒有熱交換和作功
\[Q = 0, W = 0\\ \Delta U = 0 \Rightarrow U = constant.\]絕熱自由膨脹
第三節了解自由膨脹,現在考慮在絕熱情況下氣體膨脹,沒有作任何功,就像兩個容器用一個栓連在一起,一邊有氣體,一邊沒有,此時絕熱情況下Q = 0。
接著栓打開之後就快速流向另一邊,這個快速膨脹的過程當中是非準靜的(not quasistatic and cannot be depicted on a PV diagram),因為平常的準靜模型都有一個活塞擋住XD
所以作功為零。
\[Q = 0, W = 0\\ \Delta U = 0\]在絕熱自由膨脹過程中,任何氣體(理想和真實)的內能都沒有變化!
不過雖然說內能都沒有變化,但理想和真實在實驗上還是有一些不一樣的地方
- 理想氣體:內能沒有變化,溫度也沒有變化。是因為理想氣體不考慮分子之間作用力,所以內能只有分子動能(溫度),當內能沒變化時,動能沒變化,溫度沒變化,進一步得到理想氣體的內能只和溫度有關,跟壓力還有體積無關。
- 真實氣體:內能沒有變化,但在高壓或低溫時溫度有變化。因為真實氣體除分子動能外,還要考慮分子間作用力,所以當位能改變,內能沒變時,動能需要變,所以溫度有些許變化,進一步得到真實氣體的內能會和溫度、壓力(體積)有關。
數學解釋如下
\[dU = \frac{\partial U }{\partial T} dT+\frac{\partial U }{\partial V} dV = 0\\ dU = 0, dT = 0, dV \neq 0 \Rightarrow U(T)\\ dU = 0, dT \neq 0, dV \neq 0 \Rightarrow U(V,T)\](PV是有關係的,要說$U(P,T)$也行)
當我們說「等溫」和「絕熱」的時候,路徑已經決定好了,只有唯一路徑,所以可以直接用端點看狀態來求做功。
循環路徑
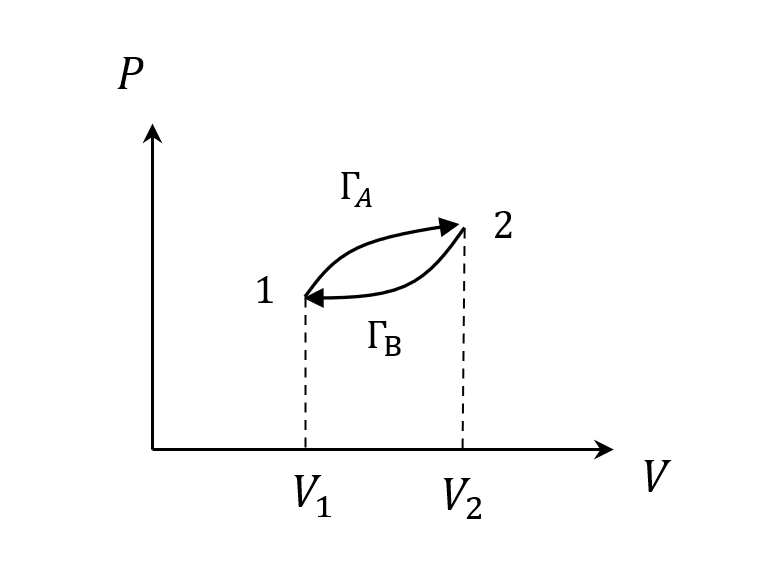
一個順時鐘的過程,$W_A > 0, W_B < 0$,淨作功 > 0,但因為回到初始狀態,所以
\[\Delta U = 0\\ Q=W\]比熱
接著來介紹比熱(Heat Capacity),通常分成定容和定壓。
- 定容比熱定義:一莫耳的氣體,在固定體積(定容)的情況下,上升1度需要的熱量。
- 定壓比熱定義:一莫耳的氣體,在固定壓力的情況下,上升1度需要的熱量。
那接下來我們分別來計算。
定容比熱
定
\[C_v\equiv\frac{1}{n}\left(\frac{dQ}{dT}\right)_v\]根據熱力學第一定律
\[Q=\Delta U + W\]轉成微分形式
\[dQ=dU+PdV\]代入定容比熱公式,因為體積不變(沒作功),所以
\[C_v=\frac{1}{n}\left(\frac{dQ}{dT}\right)_v=\frac{1}{n}\left(\frac{dU}{dT}\right)_v\]等價於看內能改變。
上一章節算過
\[U=\frac{3}{2}kT\]換成莫耳數
\[U=\frac{3}{2}nRT \Rightarrow \frac{dU}{dT} =\frac{3}{2}nR\]所以
\[C_v= \frac{3}{2}R\]只是個常數,所以這裡重點在於,不論是對哪一種理想氣體(單原子),定容比熱都是一樣的!要把它們在定容的情況下加熱一度所需要用到的熱量都是一樣的!(實驗也得證)。
理想氣體的通用比熱
複習一下定容的準靜過程,描述吸熱
\[Q_v = nC_v \Delta T\]套第一運動定律
\[W = 0\\ \Delta U = Q = nC_v\Delta T\]但在絕熱自由膨脹提到過,理想氣體的內能只和溫度有關,所以定容下是這個公式的話,那其他非定容的過程也都要是同樣的公式
This applies to any process involving an ideal gas, not just to constant-volume processes.
這個通用的內能公式只對理想氣體適用!
定壓比熱(理想氣體)
定
\[C_p\equiv\frac{1}{n}\left(\frac{dQ}{dT}\right)_p\]一樣用熱力學的微分形式
\[C_p = \frac{1}{n}\left(\frac{dU}{dT}\right)_p+\frac{P}{n}\left(\frac{dV}{dT}\right)_p\]等號右邊第一項等價於定容比熱,因為理想氣體的U(T),所以不論定壓定容還是其他,
\[U = nC_v T\]因此
\[C_p = C_v+\frac{P}{n}\left(\frac{dV}{dT}\right)_p\]而
\[PV=nRT\\ V=\frac{nR}{P}T\\ \frac{dV}{dT} = \frac{nR}{P}\]代回去
\[C_p = C_v + \frac{P}{n}\frac{nR}{P} = \frac{3}{2}R+R = \frac{5}{2}R\]小結比較
在定壓情況下,因為有一部份拿去作功,所以
\[Q_p=nC_p\Delta T\\ nC_p\Delta T = \Delta U + W\\ nC_p\Delta T = \Delta U + P\Delta V\]這個公式對所有氣體(理想和現實)都適用。
但前面說到理想氣體的性質,內能只和溫度有關,並且使用理想氣體方程式
\[P\Delta V = nR \Delta T\\ nC_p\Delta T = \Delta U + W\\ nC_p\Delta T = nC_v\Delta T + P\Delta V\\ nC_p\Delta T = nC_v\Delta T + nR \Delta T\\ C_p = C_v + R\\ C_p-C_v = R\]這個公式只對理想氣體適用!
最後我們整理知道理想氣體的定容比熱和定壓比熱關係是
\[C_p = C_v + R\]代表同樣上升一度,定壓需要用到的熱量比定容要多,而這個想一下也覺得挺合理,畢竟定壓吸收的熱有一部分都拿去作功了,所以要維持同樣的內能上升(達到的溫度差)就需要更多的熱。
因此
\[C_p > C_v\]也是一般材料的通用性質。
並且現實來說,理論上容易計算是$C_v$,實驗上容易計算是$C_p$,畢竟做實驗加熱膨脹很常見,要再額外花功夫壓回定容不好做。
另我們也定
\[\frac{C_p}{C_v}=\frac{5}{3} = \gamma\]就是我們熱平衡的章節在計算exponential decay時帶的衰減指數。
舉例:等溫膨脹 vs 絕熱膨脹
熱力學第一定律
\[\Delta U = Q-W\]系統(理想氣體)的內能改變,等於微觀作功(熱)減掉宏觀作功,這個我們通常意象的加熱微觀膨脹給的能量就是熱(Heat)。
所謂的宏觀和微觀差別就在於熱力變數(Thermodynamics variable),溫度和體積是否有可見的變化。
接下來我們要繼續討論兩個系統,等溫膨脹及絕熱膨脹。
等溫膨脹
系統溫度一樣沒有變化,所以
\[\Delta U = 0\\ W=Q=NkT\ln\left(\frac{V_2}{V_1}\right)\]所以吸熱的時候就會拿來作功做等溫膨脹($V_2>V_1$)。
那麼理想氣體方程式
\[PV=NkT\]因為等溫,所以就會是常數
\[PV=\text{const}\]就是波以爾定律。
絕熱膨脹
現在系統處在絕熱環境下,代表沒有其他的熱會進來,系統中的熱也不會出去,簡單就是說
\[Q=0\]所以熱力學第一定律得
\[\Delta U = -W\]若是膨脹,做正功,則
\[\Delta U = -W < 0\]溫度就會下降($T$↓)。
故而絕熱膨脹對外作功後系統溫度會下降。
因為現在多了溫度的變數,就不再是直接的波以爾定律,需要重新整理。
我們現在有的公式
\[\begin{cases} \Delta U = -W < 0\\ PV = NkT\\ nC_v\Delta T = \Delta U = -\int P dV\\ \gamma = \frac{C_p}{C_v}=\frac{5}{3} \end{cases}\]可是其實滿難解的,因為我們只有兩條公式,理想氣體是代數方程,定容是積分式,然後有三個變數$P,V,T$未定,所以我們換個想法,改求微分式$dP,dV,dT$。
(這裡有個概念,通常取微分之後,因為微分和微分相乘都會是很小的數字通常可先忽略,這時很容易就可以有一些線性關係出來,然後求微分方程就好了。)
所以理想氣體方程
\[d(PV)=d(NkT)\\ VdP+PdV=NkdT=nRdT\]定容積分式
\[nC_v dT = -PdV\](兩邊同取積分其實就回到原本的($\because \int nC_vdT=nC_v\Delta T$)。
接著前者乘上$C_v$,後者乘上$R$,得到
\[\begin{align} C_v VdP &+ C_v P dV - nC_v R dT = 0\\ &+RPdV+nC_vRdT = 0 \end{align}\]兩者相加得
\[C_vVdP+(C_v+R)PdV = 0\\ C_vVdP+(C_p)PdV = 0\\ VdP+\frac{C_p}{C_v}PdV = 0\\ \frac{dP}{P}+\gamma \frac{dV}{V}=0\]就是微分方程式了,接下來來解。
先統一積分,從原先狀態到後面狀態
\[\int_1^2 \frac{dP}{P}+\gamma \frac{dV}{V}=0\\ \ln P \bigg|_1^2+\gamma \ln V\bigg|_1^2=0\\ \ln \frac{P_2}{P_1}+\gamma \ln \frac{V_2}{V_1}=0\\ \ln \frac{P_2}{P_1}+\ln \left(\frac{V_2}{V_1}\right)^\gamma=0\\ \ln \left(\frac{P_2}{P_1}\left(\frac{V_2}{V_1}\right)^\gamma\right)=0\\ \left(\frac{P_2}{P_1}\left(\frac{V_2}{V_1}\right)^\gamma\right) = 1\\ P_2 V_2^\gamma = P_1 V_1^\gamma = \text{const}\]至此我們得到結果
\[PV^{\frac{5}{3}}=\text{const}\]驗證
這裡稍微驗證一下,我們代入作功
\[W=\int_{V_1}^{V_2}PdV=\text{const}\int_1^2\frac{dV}{V^{\gamma}}=\text{const}\frac{V_2^{(1-\gamma)}-V_1^{(1-\gamma)}}{(1-\gamma)}\]又
\[P_2 V_2^\gamma = P_1 V_1^\gamma = \text{const}\]反正都是一樣的常數,所以再代回去得到
\[\text{const}\frac{V_2^{(1-\gamma)}-V_1^{(1-\gamma)}}{(1-\gamma)}=\frac{1}{1-\gamma}[P_2V_2-P_1V_1]=\frac{1}{\gamma - 1}[nRT_1-nRT_2]\\ \Rightarrow W=\left(\frac{nR}{\gamma-1}\right)(T_1-T_2)\\ \frac{nR}{\gamma-1}=\frac{nR}{\frac{C_p}{C_v}-1}=nR\frac{C_v}{C_p-C_v}=nR\frac{C_v}{R}=nC_v\\ \Rightarrow W = nCv(T_1-T_2)\]然後之前的內能和定容關係式
\[\Delta U = nC_v (T_2-T_1)\]的確以上兩個對比符合熱力第一定律(絕熱系統下$Q=0$)
\[\Delta U = -W\]比較
這裡畫個圖比較一下兩條曲線,注意一樣底下面積就是各自的作功
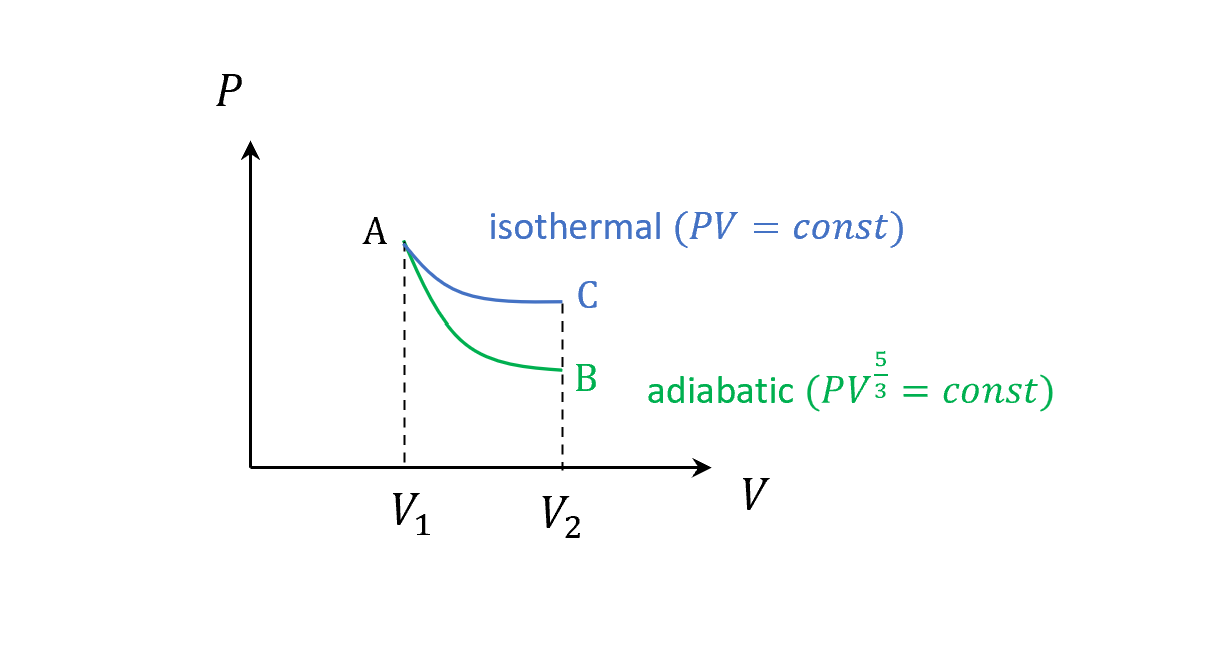
這個圖也可以用另外一種推導方式如下,絕熱情況
\[PV^\gamma = constant\\ \gamma = \frac{C_p}{C_v}\]以及
\[V^\gamma dP + \gamma P V ^{\gamma - 1}dV = 0\\ \frac{dP}{dV} = -\gamma \frac{P}{V}\]等溫的話,直接用理想氣體方程式
\[PV = nRT\\ PdV+VdP = nRdT = 0\\ \frac{dP}{dV} = -\frac{P}{V}\]因為$\gamma > 1$,所以絕熱的線會比等溫還要陡。
進階: 多原子比熱
以上的比熱都是在算單原子理想氣體情況。
目前我們已經知道溫度是平均動能,而理想氣體模型就是structless hard spheres with only translational kintetic energy,那麼理想氣體的總能量(假設N個)就是
\[U=N\left(\frac{1}{2}m v^2\right) = \frac{3}{2}NkT\](這個跟我們在章節絕熱自由膨脹的結論一樣,理想氣體的內能只和溫度有關。)
但這其實都只是在描述單原子理想氣體(只算平移動能)的情況,如果需要考慮多原子,那就得再得考慮更多自由度,但在說這個之前,必須要先說到能量均分定理。
能量均分定理
前面在講的平移平均動能,若
\[\frac{1}{2}m \bar v^2 = \frac{3}{2}kT\]分成三維之後,那就各自是$\frac{1}{2}kT$。
從這裡我們引入自由度的概念
A degree of freedom of a molecule is a way in which it can possess kinetic or potential energy. In the mathematical expression for the total energy, each degree of freedom appears as an independent term that involves the square of a position coordinate or a velocity component.
這樣將能量均分的稱作 equipartition of energy
Each degree of freedom has an average energy 1/2kT
自問的問題:為什麼一定可以均分?
在古典物理的範疇內,對於一個處於熱平衡的系統,能量之所以會均分給所有「可用的」自由度,是因為:
- 從機制上看: 分子間的隨機碰撞是能量在不同運動模式間交換的途徑。
- 從統計上看: 能量均勻分配的狀態是壓倒性最可能出現的宏觀狀態(熵最大)。
但這個「一定」是有限制的,當溫度太低,量子效應顯現時,某些自由度會被「凍結」而無法參與能量的均分。
接下來我們來考慮轉動和振動的部分。
轉動動能
想像一個分子是dumbbell的形狀的雙原子,當分子互相碰撞的時候,除了之前的平移動能變化,部分也會變成該分子的轉動動能,然後一樣這個過程會達到某種平衡的狀態,能量可以均分轉動的自由度。
一般來說,轉動一樣分三維,可是就像啞鈴,如果繞著啞鈴本身自己的軸轉的話,從
- 古典來說,轉動慣量太小,因為半徑太小,所以幾乎可以忽略(但不是本質的原因,畢竟可以忽略的數量級標準要怎麼定?或者說可以提高轉速來彌補轉動慣量的小)
- 量子來說,這才是真正的本因,從能量量子化出發,要啟動一個轉動模式,需克服一定門檻,$E=\hbar^2/I$,若I太小,能量所需就會非常大了,所以啞鈴本身轉軸的I的確很小,需克服的E大到難以克服。這個公式可以從薛丁格方程式推導出來,這裡暫且跳過。
所以我們討論轉動的自由度時,只會有兩個維度。
能量均分下,總能量就是,平移三個加上轉動兩個得
\[U = 3(\frac{1}{2}kT)+2(\frac{1}{2}kT) = \frac{5}{2}kT\]代入定容比熱,得到
\[C_v = \frac{5}{2}R\] \[C_p = \frac{7}{2}R\]振動動能
接著若氣體分子度完全是rigid得狀態,想像原子間有個彈簧,受到撞擊的時候還會有些震盪,那麼除了前面的平移和轉動,我們還得考慮振動的自由度。
振動的自由度,包含動能和位能,有兩個自由度(固體的話,三維晶格就共算六個自由度),併在一起計算
\[U = 3(\frac{1}{2}kT)+2(\frac{1}{2}kT)+2(\frac{1}{2}kT) = \frac{7}{2}kT\]比熱
\[C_v = \frac{7}{2}R\\ C_p = \frac{9}{2}R\]能量均分定理的限制
但是其實這些都考慮進去之後,也沒有完全反映現實得到的結果。
主要的原因在於「溫度」。
不是所有溫度下,都可以把平移、轉動、振動的自由度考慮進去,他們有一個溫度範圍。
譬如說可能低溫時,只需要考慮平移,再高溫一點才能列入轉動,最後更高溫才需要考慮振動。
這個的本質跟量子力學有關,前面提到的能量量子化,就是看當下的溫度能不能越過該能量的門檻。
