Cjue25

Good things take time

在學熱力學的時候，通常起手就是畫一個容器，裡面有一堆氣體分子，旁邊有個活塞擋住，然後容器下面加熱，進而探討各種狀態和路徑。

但我想要先連結熱力學在日常上的應用，最好的簡單例子就是蒸汽機。

蒸汽機有很多種類，但共同原理就是：燃燒某種燃料(例如煤)，產生的熱可以將周圍的水加熱至沸騰，產生的蒸汽推動活塞，活塞連結到的機械裝置(例如輪子)就可以跟著移動，活塞也來回移動，將熱能轉換為動能。

可以參考這個Youtube影片How Do Steam Locomotives Work - Steam Engines Explained How Do Steam Locomotives Work - Steam Engines Explained

如此一來再回來看我們學熱力學常見的簡單模型就更有感覺了。接下來就針對這個模型(系統)，先了解一些常用的名詞定義，下一節我們就會進展到熱力學第一定律了。

簡單系統

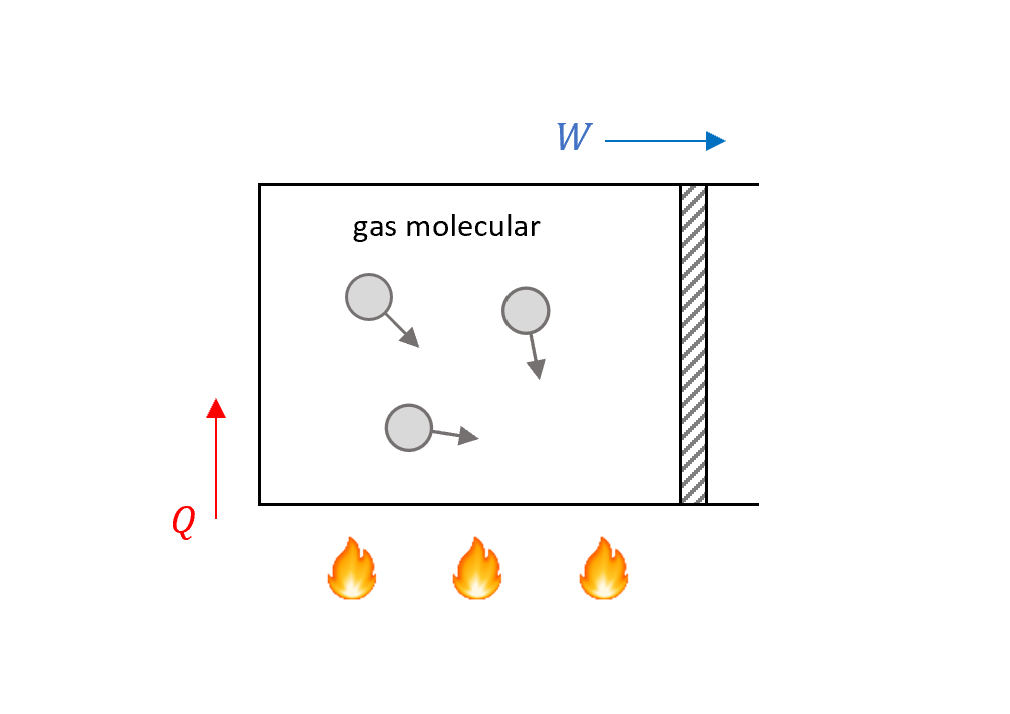
現在考慮有一盒氣體，開口處有活塞可以動，氣體可以對外面做功($W$)。

\[W:\text{work done by the gas}\]

把這個系統放在火爐上加熱，底下會有熱量從火爐給氣體分子，在這裡我們定義$Q$正為吸熱，負會放熱

\[Q:\text{heat absorbed by the gas}\]

系統名詞定義

熱庫

底下在加熱的火爐視為一個熱庫，熱庫的性質

  • 擁有非常大的比熱。
  • 大量熱可以流入流出，但不改變該系統溫度。
  • 實際舉例：巨大湖泊、大氣層、一直被加熱的恆溫爐子
  • 常見迷思：熱庫不是”含有很多的熱”，記住heat不是狀態含量(第一節)。

準靜系統 (quasistatic)

現在討論的熱力學系統是準靜系統，系統是氣體，外界環境就是包著的容器和活塞。

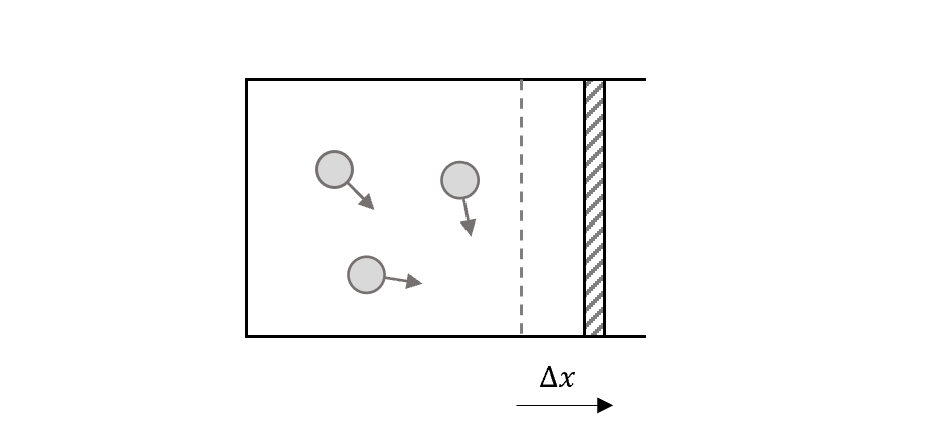
如果氣體膨脹，將活塞推出去，那就是氣體對外界作功，若這個系統和外界環境的熱力學變數$(P, V, T, n )$都變化地非常緩慢(infinitely slowly)，就稱這個作功的過程為準靜的(quasistatic)，代表系統任意時候都非常接近於平衡態(equilibrium state)，可以由一組宏觀熱力學變數去定義和描述。

要達到這件事情，我們可以簡單想像譬如說活塞因為重力(或其他力)，抵抗氣體的向外膨脹的壓力。如果活塞很快速地移動，那麼整個快速膨脹的過程就會有一些turbulence，局部狀態差異大，系統的壓力狀態就沒辦法被唯一定義下來。 (這種唯一的定義是說，整個系統每個空間的狀態都是一樣的，通常如果不是的話，對這個系統沒辦法只用某組特定數值定義)

不過實務上，其實也不是說真的要達到infinitely slowly，重點是過程每個階段都等到系統達到其平衡狀態，過程的時間尺度都能超過該系統自己達成平衡時需要的relaxation time。

作功

熱力學討論的作功是系統對外作功(external)，定義方向為+，並不考慮系統內部自己作的功(internal)。

因此在準靜系統中，系統對活塞的作功就是

\[dW = Fdx = (PA) dx = PdV\]

PV圖

因為準靜過程的P和V都能夠被唯一定義(uniquely defined)，所以能畫個PV圖。

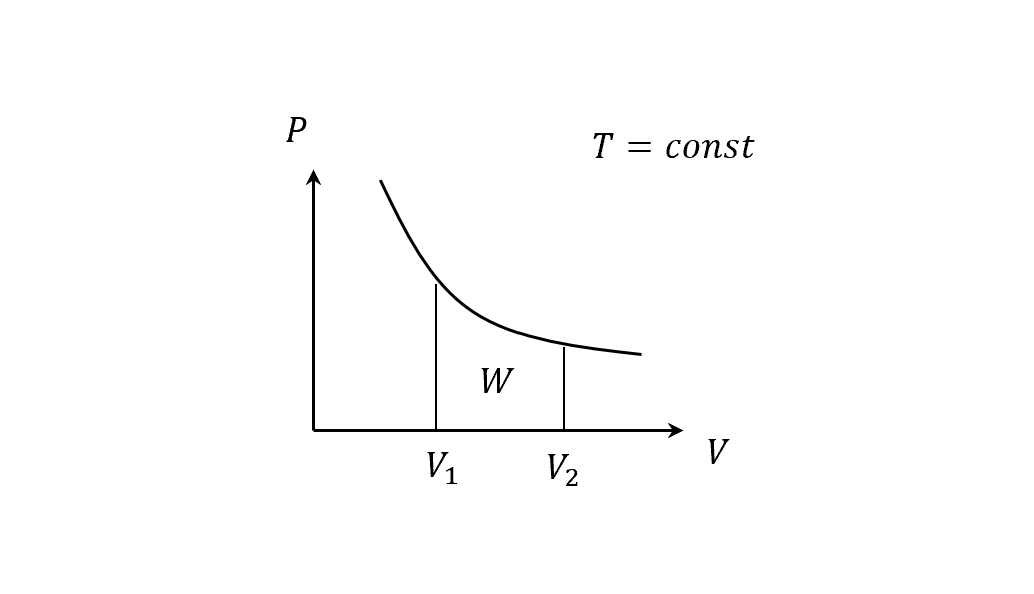
在 PV 圖上

  • 一個「點」代表一個「狀態」，例如$P, V, T$和之後會提到的內能$U$。
  • 一條「線」代表一個「過程」，例如$Q, W$，數值取決於經過的路徑，像是從平衡態(1)到另一平衡態(2)的過程，積分底下的面積就是系統對外的總作功了(這裡也很容易理解作功跟路徑過程有關)。

自由膨脹(Free Expansion)

相較於前面的準靜系統，現在就單純只有一個絕熱容器，不考慮外界環境。然後裡面用一個膜隔開空間，其中一個空間都裝著氣體。

若把膜戳破，氣體膨脹，但因為沒有之前的活塞，所以氣體沒有做任何的功，這就叫做free expansion。

實驗上，理想氣體在這樣的自由膨脹過程中，溫度不會變化。

可逆與不可逆

可逆過程的三大條件

  • 必須是準靜過程
  • 過程沒有摩擦力
  • 熱交換必須在等溫且溫差趨近0條件下進行 (不然返回勢必要有其他做功，還不能100%返回)

現實生活中都是不可逆的，舉凡爆炸、擴散、傳導、化學反應等等，系統大部分會處在混亂的非平衡狀態，所以不能畫出PV圖，因為你根本不知道路徑應該會長什麼樣子。

而特別指出摩擦力的原因是，譬如我們搓手生熱，可以簡單分成兩部分，肌肉作功讓手(系統)提高系統內能(溫度)，接者手和環境的溫差讓熱流向環境，手的溫度就會下來了，整個過程我們就稱為產生”廢熱”到環境中。

而會稱為這是廢熱的原因，則是若你想把這個環境的熱在拿回來，讓手回到原始的狀態，勢必得要再額外作功(就像是沒有完美冷機)，改變系統(手)以外的環境狀態，所以整體來講並沒有辦法”可逆”如同影片倒帶一樣全部一起回到一樣的原始狀態。

最後第三點也是類似的道理，一旦兩個系統有顯而易見的溫差，那麼熱庫流向冷庫互相達成平衡之後，若要從冷庫在抽取熱回給熱庫讓兩者回到原始狀態，勢必得要有其他作功，改變了另外一個環境系統的狀態，所以是不可逆的。

理想氣體

氣體若遵守以下氣體方程式，我們就稱為理想氣體，現在系統內部的氣體通常假設為理想氣體(ideal gas)，處理起來比較簡單，因為這個方程式就是簡單的線性關係。

現實中的氣體當然不會是這樣線性的關係，不過若現實的氣體密度夠低，沒有達到液化的溫度，那就可以用理想氣體方程式。

一般在大氣壓和室溫下的氣體可以近似於理想氣體。

理想氣體方程式

  • Boyle：發現同溫度時PV成反比得到$PV=constant$
  • Charles & Gay-Lussac：發現定壓時，體積和溫度成正比$V\propto T$；定容時，壓力和溫度成正比$P\propto T$

綜合結果，得到

\[PV=NkT\\ PV = nRT\]

You may also enjoy