(6) 熱力 ─ 引擎 & 效率
第三節我們提到了蒸汽機,第五節我們提到了PV圖的路徑,現在結合這兩者,如何在PV圖上表達一個引擎的概念?
所謂引擎,就是將其他能轉成機械能,然後透過連結的裝置「反覆」運轉的機器。
An engine or motor is a machine designed to convert one or more forms of energy into mechanical energy.
譬如說不可能你的機車小爆炸之後只能發動一次,然後跑一公尺就停下來了,一定是因為反覆運轉,回到原始狀態後再做一次功,才能讓車子持續前進。
所以在PV圖裡,我們可以用「循環路徑」來表示,路徑代表了熱和功的過程,循環代表可以回到原本的狀態,達到引擎可以反覆運轉的概念。這樣的循環路徑我們稱為Thermal Cycle。
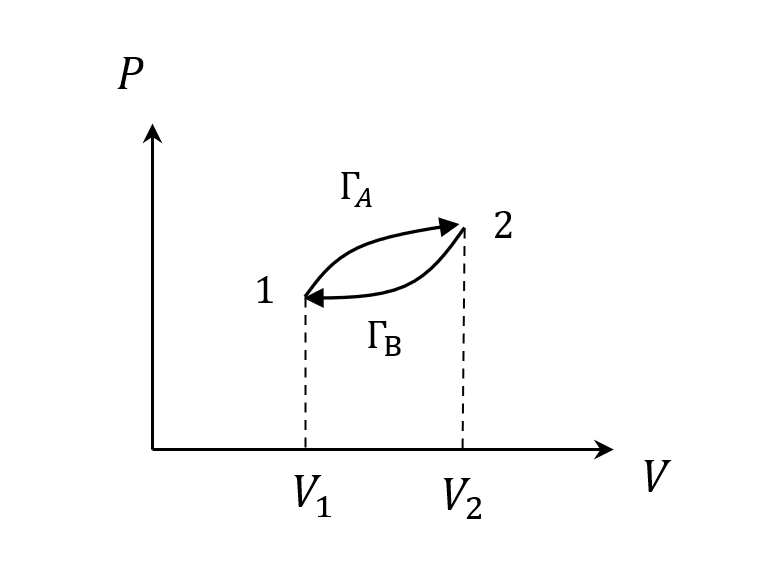
接著卡諾就提出了一個問題:
「那這世界有沒有最好、效率最好的引擎呢?」
這節我們就來細看這個問題。
卡諾引擎
假設是在可逆、理想氣體、無摩擦力的狀況下,卡諾得到結論的最好引擎的Thermal Cycle長這樣,由兩條等溫線和兩條絕熱線所組成
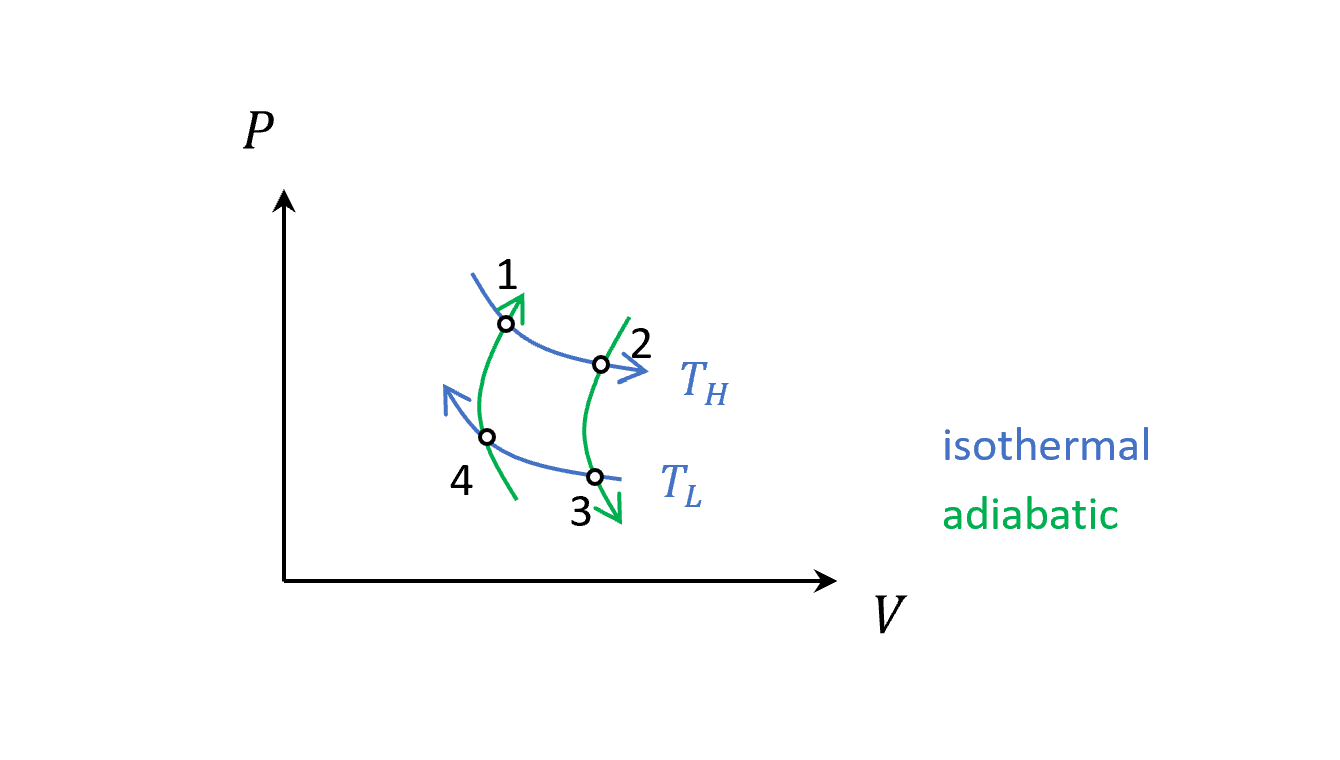
- 跟熱庫接觸,等溫膨脹,這時內能不變,氣體吸熱並對外做功。
- 熱庫被移除,系統在絕熱環境,然後做絕熱膨脹,對外做功,內能下降,溫度下降。
- 跟冷庫接觸,等溫壓縮,這時內能不變,氣體放熱並對內做功(壓縮)。
- 冷庫被移除,系統在絕熱環境,然後做絕熱壓縮,對內做功,內能上升,溫度上升。
算四段作功
\[\begin{cases} W_{12}=\int PdV = nR T_H \ln \left(\frac{V_2}{V_1}\right)\\ W_{23}=\left(\frac{nR}{\gamma-1}\right)(T_H-T_L) = n C_v(T_H-T_L)\\ W_{34}=nRT_L \ln\left(\frac{V_4}{V_3}\right) = nR T_L \ln\left(\frac{V_1}{V_2}\right) = -nRT_L\ln\left(\frac{V_2}{V_1}\right)\\ W_{41}=nC_v\left(T_L - T_H\right) \end{cases}\\\]等溫: $$ P_1V_1=P_2V_2\Rightarrow \frac{P_1}{P_2}=\frac{V_2}{V_1}\\ P_3V_3=P_4V_4\Rightarrow \frac{P_3}{P_4}=\frac{V_4}{V_3}\\ \Rightarrow \frac{P_1P_3}{P_2P_4}=\frac{V_2V_4}{V_1V_3} $$
絕熱: $$ P_1V_1^\gamma=P_4V_4^\gamma\Rightarrow \frac{P_1}{P_4}=\frac{V_4^\gamma}{V_1^\gamma}\\ P_2V_2^\gamma=P_3V_3^\gamma\Rightarrow \frac{P_3}{P_2}=\frac{V_2^\gamma}{V_3^\gamma}\\ \Rightarrow \frac{P_1P_3}{P_2P_4}=\left(\frac{V_2V_4}{V_1V_3}\right)^\gamma $$ 結合在一起: $$ \left(\frac{V_2V_4}{V_1V_3}\right)^\gamma = \frac{V_2V_4}{V_1V_3}\\ \left(\frac{V_2V_4}{V_1V_3} =\right)^{\gamma-1}=1,\quad \gamma \neq 1\\ \frac{V_2V_4}{V_1V_3} = 1 $$
我們算一下熱量,兩條絕熱就不用算了,兩條等溫($\Delta U = 0$)
\[W_{12}=Q_H=nR T_H \ln \left(\frac{V_2}{V_1}\right)\\ W_{34}=Q_C=-nRT_L \ln \left(\frac{V_2}{V_1}\right)\]再計算熱量除以溫度後的積分(這其實就是熵的定義,後面會再細談)
\[\oint \frac{dQ}{T}=\frac{Q_H}{T_H}+0+\frac{Q_C}{T_L}+0\\ =nR\ln \left(\frac{V_2}{V_1}\right)-nR\ln\left(\frac{V_2}{V_1}\right)\\ =0\]因此得到
\[\frac{Q_H}{T_H}+\frac{Q_C}{T_L}=0\]代表作功$1\to 2$的時候是吸熱,$3\to 4$的時候是放熱,高溫吸過來的熱是正比於$T_H$,低溫放出去的熱也是正比於$T_L$,這個引擎就會非常簡單,四個行程裡只有兩個有吸熱和放熱。
效率
這個回到原點的封閉曲線,溫度不變,總對外做功為(圈起來的面積)
\[W=|Q_H|-|Q_C|\]而引擎的Efficiency定義:輸出的功除以吸的熱,若吸進來的熱能完全做功,是最好(但當然不可能)。
\[\epsilon = \frac{W}{Q_{in}}\]所以
\[\epsilon =\frac{Q_H-|Q_C|}{Q_H}=1-\frac{T_L}{T_H},\quad 0<\epsilon < 1\\ (\because \frac{Q_H}{T_H}+\frac{Q_C}{T_L}=0)\]所以如果你的引擎的低溫高溫固定下來,設計出來能夠達到最高效率就是這個值,也稱為 Carnot Efficiency,效率只和冷庫熱庫的溫度有關。
Heat Engine Diagram
除此之外,卡諾從觀察水車出發,知道水車就是靠水流讓最高點和最低點有一個重力位能差,再把這個能量轉換成功。他把這個概念用到了引擎上,提出一個抽象的Diagram
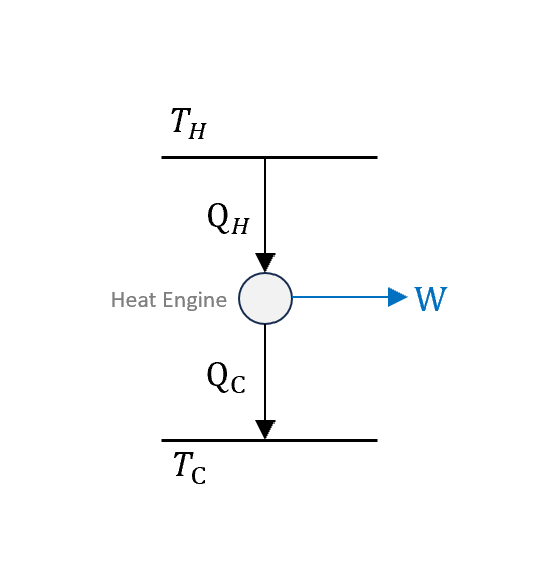
$Q_H$是輸入,中間灰色圈圈是熱機(注意是個cycle),一部份會對外做功$W$,一部份會當廢氣排出$Q_C$。
我們可以把這個抽象的圖和之前$P-V$圖做結合
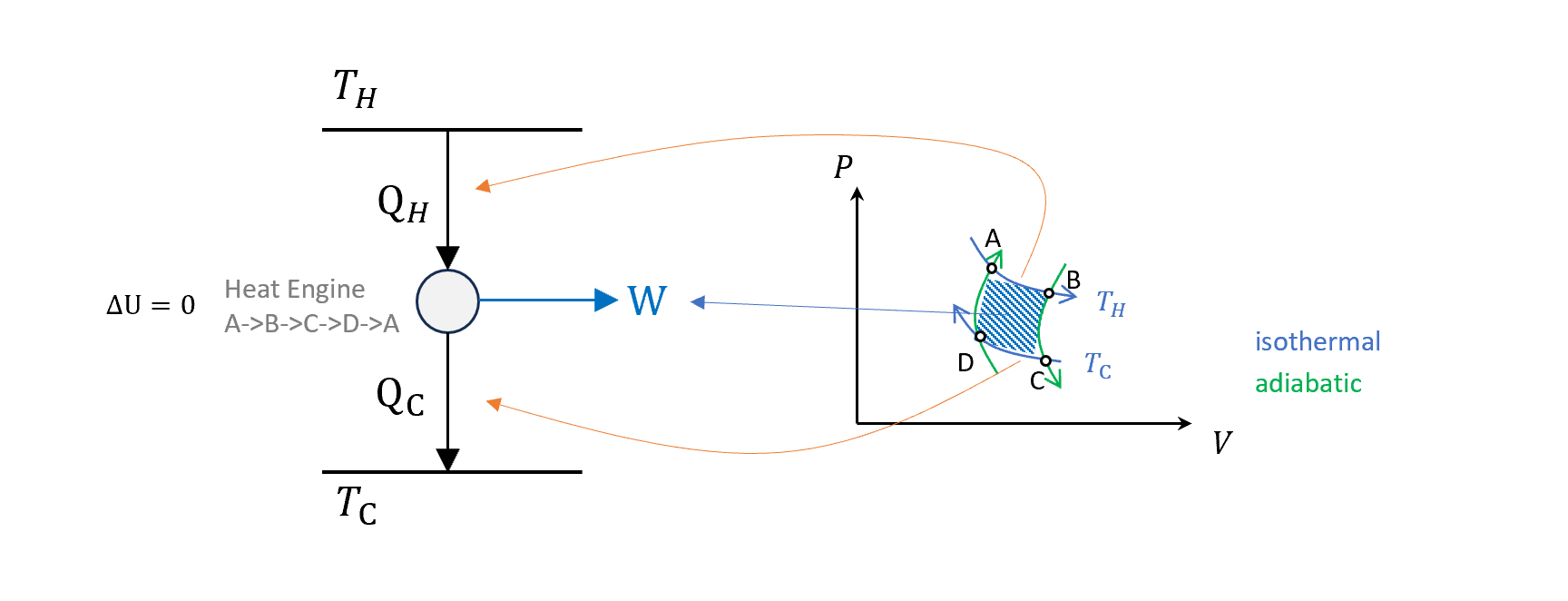
- \(A\to B\to C\to D\to A\)為一熱機循環,代表diagram中間灰色的圓圈。
- \(PV\)圖圍起來的面積就是對外輸出的功$W$。
- 循環一圈回來總內能不變,所以灰色圓圈的內能不變。
- \(A\to B\)等溫線,內能不變,對外界做功,吸熱,代表$Q_H$。
- \(C\to D\)等溫線,內能不變,外界對其做功,放熱,代表$Q_C$。
- \(B\to C、D\to A\),都是絕熱線,為了能夠完成循環。
完美熱機?
那麼到這裡不曉得你有沒有疑惑,為什麼剛剛在算效率的時候一定有一個$Q_C$的存在呢?
如果沒有的話效率不就100%了嗎?最好的引擎只有卡諾引擎了?沒有真正的完美熱機嗎?
若真的要設計出完美熱機,那就是要設計出這樣(但這個在熱力學第二運動定律下,是不可能的。我們會在之後的章節更進一步討論熱力學第二定律 )
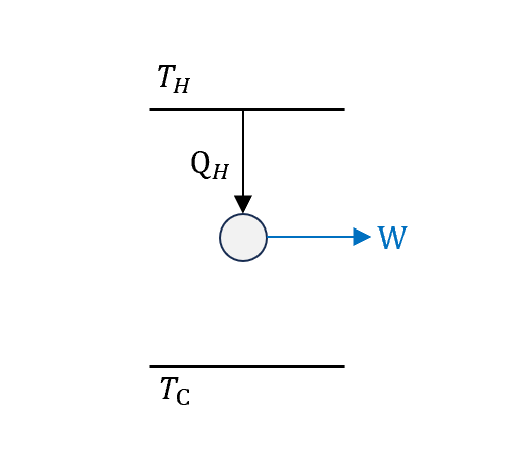
這裡延伸一下,若只是單純看一條等溫線
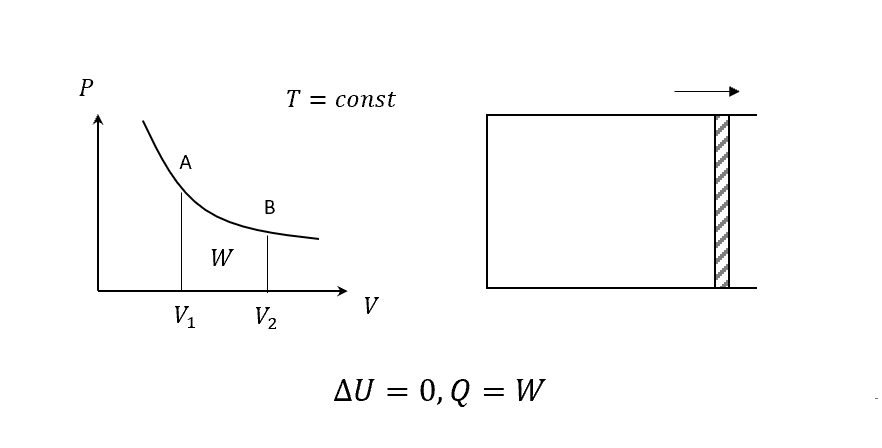
要只有這樣的過程,代表熱機只會動一次,那麼可以效率的確可以=1。
但我們所謂的"cycle engine",是要回到原本的state,以現在這張圖來說就是B還要再回到A,有這樣的cycle我們才會去談熱力學第二運動定律,才會進一步證明出熱力學第二運動定律告訴我們不可能有完美熱機的存在。
完美冷機?
那都有完美熱機的想法了,那應該就會有完美冷機的想法了吧!
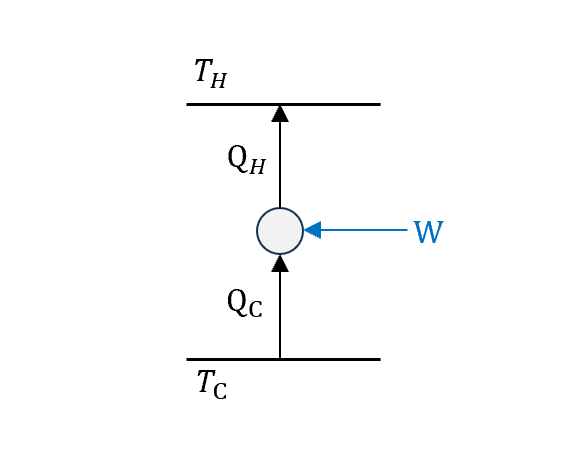
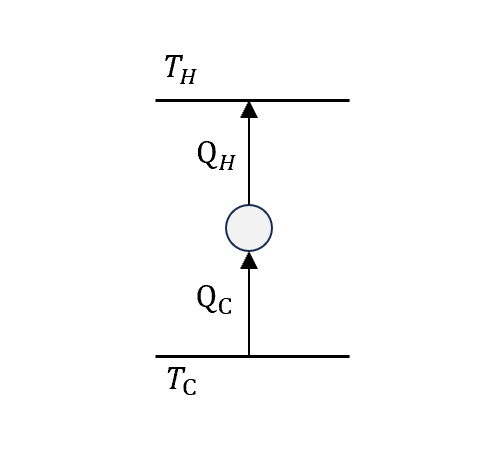
先看一般的,把一般熱機的圖反過來就是冷氣機,看把熱流pump上去要做多少功,讓熱流從低溫到高溫
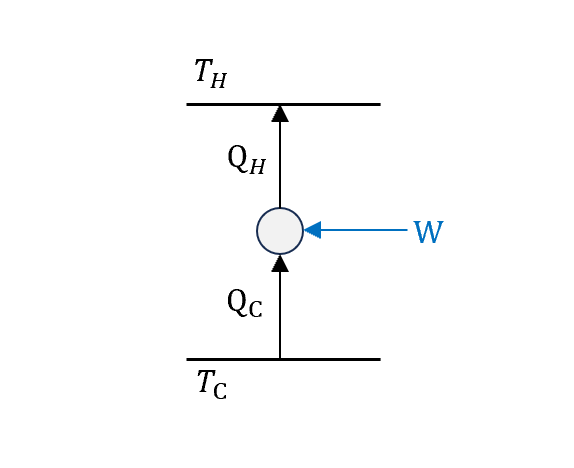
所以公式
\[Q_H=W+Q_C\]一樣來算一下效率(coefficient of performance, COP)
\[COP\equiv \frac{Q_C}{W}=\frac{Q_H-W}{W}=\frac{Q_H}{W}-1=\frac{1}{\epsilon}-1\\ 0<\epsilon < 1,\quad 0<COP<\infty\]若要達成完美冷機,那就是不需要做任何功,相當於冰箱不用插電,光是放在那邊他就能自己從低溫流向高溫,冰箱自己一直變冷,把熱往外排。
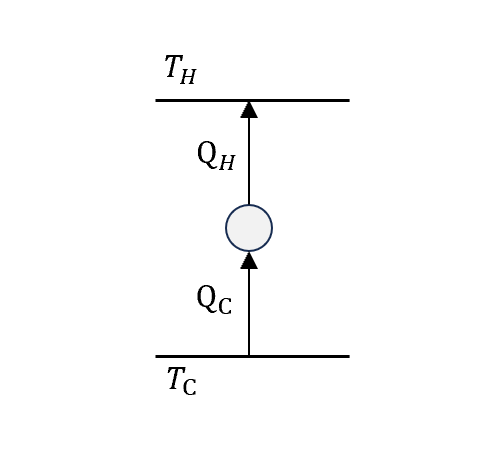
(一樣在熱力學第二運動定律下,是不可能的。)
完美熱機和完美冷機真的存在嗎?
從上面兩者來看,其實完美熱機和完美冷機是同一件事情,卡諾說要嘛真的能一起存在,要嘛一起不存在。
而我們現在的結論是後者,所以來證明一下,我們引進兩個statement:
- Kelvin-Planck Statement:完美熱機不存在。
- Clausius Statement:完美冷機不存在。
這兩者其實是等價的,要嘛一起對,要嘛一起錯。
證明一:假設Clausius是錯的
若Clausius是錯的,代表我們有完美冷機,那我們可以把一個完美冷機和一般熱機放在一起如圖
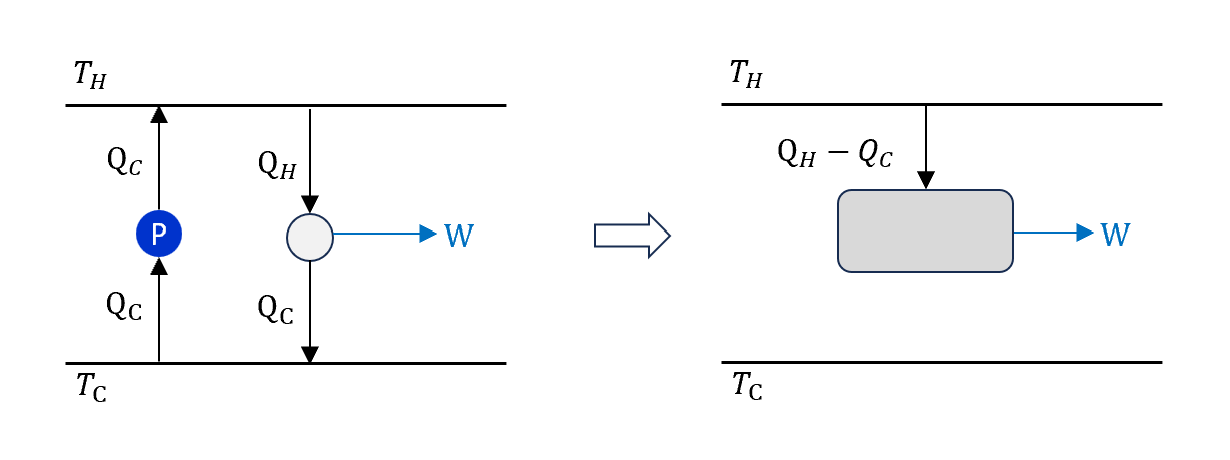
合併起來可以視為一個完美熱機,那就會變成是”完美冷機 + 一般熱機 = 完美熱機”,這樣Kelvin-Planck就錯了。
若Clausius是錯的,Kelvin-Planck就是錯的。
證明二:假設Kelvin-Planck是錯的
若Kelvin-Planck是錯的,代表我們有完美熱機,那我們可以把一個完美熱機和一般冷機放在一起如圖
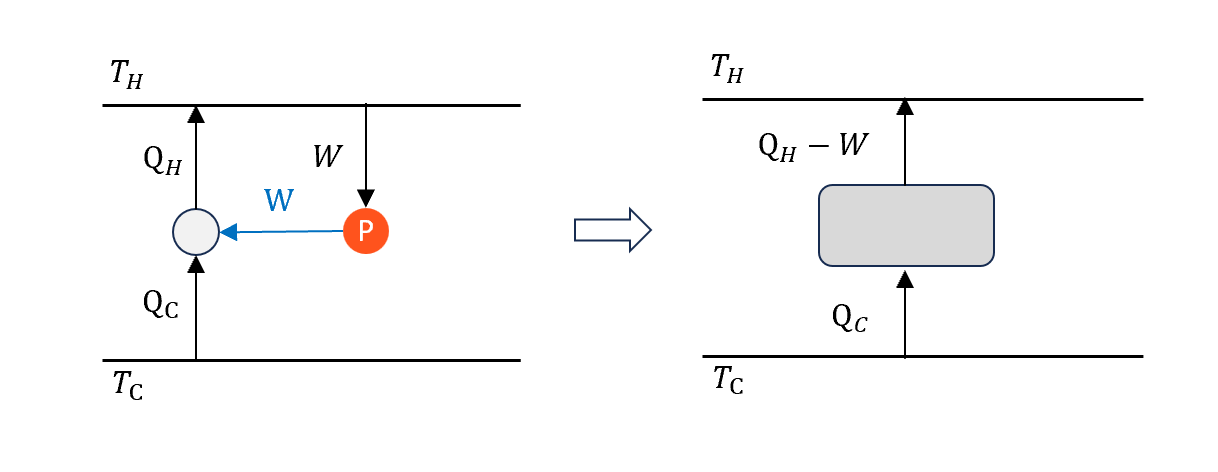
合併起來可以視為一個完美冷機,那就會變成是”一般冷機 + 完美熱機 = 完美冷機”,這樣Clausius就錯了。
若Kelvin-Planck是錯的,Clausius就是錯的。
所以數學上我們可以把這個等價關係寫成
Kelvin-Planck Statement $\equiv$ Clausius Statement
證明都不存在
目前科學認知就是Kelvin-Planck和Clausius都是對的,沒有完美冷機也沒有完美熱機。
因此整理一下思緒,我們從熱機出發,講到冷機,再來定義出何謂完美熱機、完美冷機,但是從Kelvin-Planck Statement 和 Clausius Statement知道,沒有完美熱機也沒有完美冷機,其中沒有完美冷機就代表熱無法自己從低溫流向高溫,只能從高溫流向低溫(這就是熱力學第二運動定律的其中一種描述方式。)
引擎小結
定義熱流進引擎為+,流出為-,引擎回到原始狀態所以內能變化為0。
\[\Delta U = Q-W = 0\\ W=|Q_H|-|Q_C|\]| 項目 | 熱機 | 冷機 |
|---|---|---|
| 一般 | 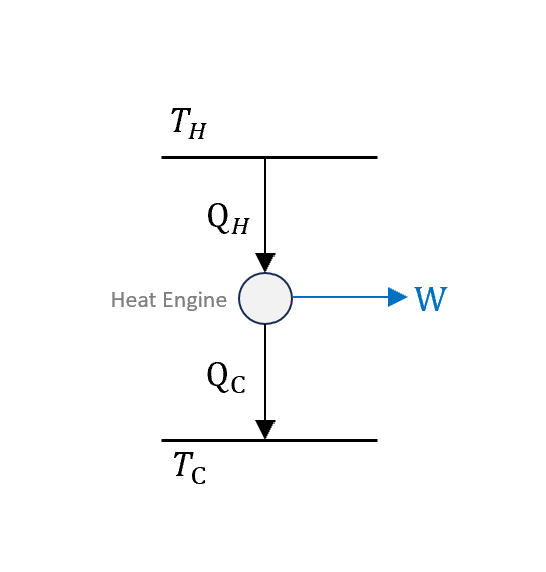 |
 |
| 完美但不存在 | 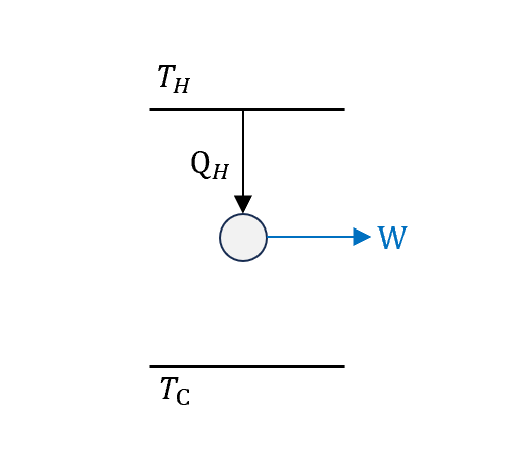 |
 |
| 效率 | 熱機效率定義為吸進來的熱能做多少功 \(\epsilon =\frac{W}{\lvert Q_H \rvert}=\frac{\lvert Q_H \rvert-\lvert Q_C \rvert}{\lvert Q_H \rvert}=1-\frac{\lvert Q_C \rvert}{\lvert Q_H \rvert}\) \(0\le\epsilon\le 1\) |
這裡是外界對系統作功,所以是負號,寫成 \(-\lvert W_{in} \rvert= \lvert Q_C \rvert - \lvert Q_H \rvert \Rightarrow \lvert Q_H \rvert = \lvert W_{in} \rvert + \lvert Q_C \rvert\) 定效率COP Refrigerator:作的功能吸走多少熱量 \(COP = \frac{\lvert Q_C \rvert}{\lvert W_{in} \rvert }\) Heat Pump:作的功能放出多少熱量 \(COP = \frac{\lvert Q_H \rvert}{\lvert W_{in} \rvert }\) |
沒有完美冷機就代表熱無法自己從低溫流向高溫,只能從高溫流向低溫。
卡諾理論
卡諾有兩個理論,也都是基於這樣的結果
- 所有可逆的(沒有摩擦等等)熱機在同一溫度差的系統中效率都一樣,效率只和哪兩個熱褲的溫度有關係,和其中細節沒有關係。
- 沒有任何熱機的效率可以好過卡諾引擎。
我們來繼續證明這兩點。
假設現在有兩台可逆熱機,其中一台(primed)逆轉變成冷機,如圖
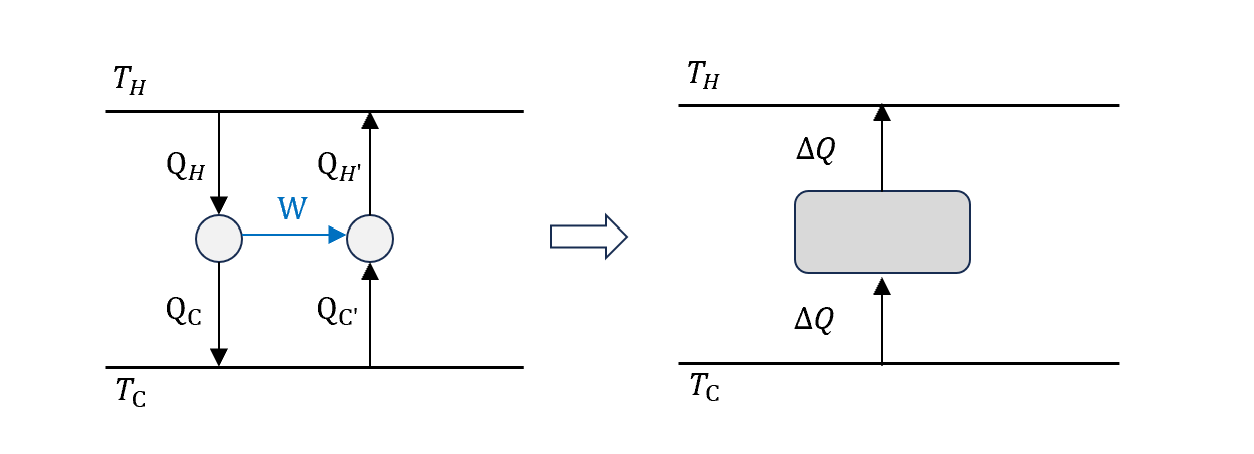
第一運動定律告訴我們
\[\Delta Q=Q_H'-Q_H=Q_C'-Q_C\]第二運動定律告訴我們
\[\Delta Q \le 0\]=0的話就代表不流,<0就代表高溫往低溫流。
所以算各自的效率,可以看出可以逆過來的那台引擎效率會比較高。
\[\begin{cases} \epsilon = \frac{W}{Q_H}\\ \epsilon'=\frac{W}{Q_H'} \end{cases}\] \[\because Q_H'-Q_H \le 0,\quad Q_H'\le Q_H\\ \Rightarrow\epsilon' \ge \epsilon\]一樣地,我們把primed的機器維持熱機,換成另外一台逆轉
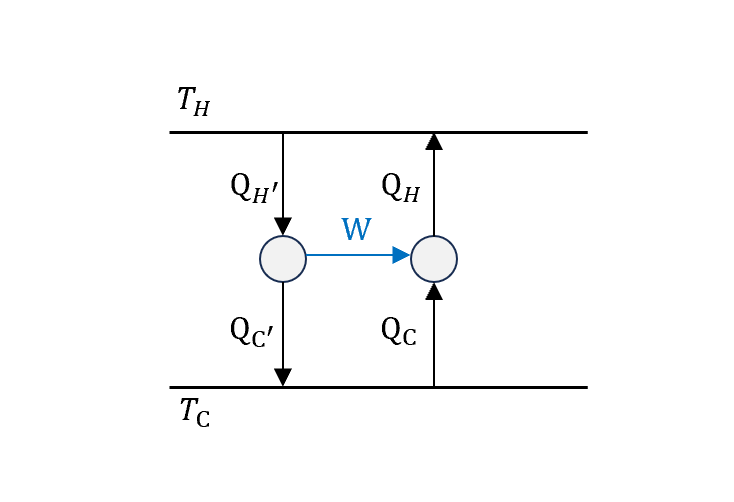
同樣證明可以得到逆過來比較高
\[\Rightarrow\epsilon \ge \epsilon'\]那合併以上就得到
\[\epsilon = \epsilon'\]證明卡諾理論的第一點,從熱力學第二運動定律的熱只能從高溫流到低溫出發,推導得在兩個熱庫之間,可逆的熱機效率都一樣,效率只跟溫度有關。
\[1-\frac{T_C}{T_H}\]那第二點其實也同理,一樣比較兩台,一台不可逆維持熱機,一台可逆轉成冷機,那可逆的(卡諾引擎)一定效率大過不可逆的
\[\epsilon_{carnot}=\epsilon_{reversible}\ge\epsilon_{irreversible}\]就一樣證明第二點了,熱力學第二運動定律這世界上只分成兩種引擎,卡諾跟非卡諾,而卡諾就是最好的引擎。
