(8) 軌道 Newton ─ Laplace-Runge-Lenz Vector
Gravitational Field EOM 的守恆量
Gravitational Field 的 EOM
\[\frac{d\vec{p}}{dt} = -\frac{k}{r^2}\vec{r}\]角動量守恆
用 $\vec{r}$對上式作外積，等號右邊為零，所以
\[0 = \vec{r} \times \frac{d\vec{p}}{dt}= \frac{d}{dt}(\vec{r}\times\vec{p}) - \frac{d\vec{r}}{dt} \times \vec{p}\]又因
\[\vec{p} = m\frac{d\vec{r}}{dt}\]所以拆開後的第二項消掉，得角動量守恆。
\[0= \frac{d(\vec{r}\times\vec{p})}{dt}\\ \Rightarrow \vec{r} \times \vec{p} \equiv \vec{L} \text{ conserved }\]Laplace-Runge-Lenz Vector 守恆
現在換另一種外積的方法、讓 EOM 對 \(\vec{L}\) 做外積
\[\begin{align} \frac{d\vec{p}}{dt} \times \vec{L} &= -\frac{mk}{r^2} \hat{r} \times \left(\vec{r} \times \frac{d\vec{r}}{dt}\right)\\ &= -\frac{mk}{r^2} \left[\vec{r} \left(\hat{r} \cdot \frac{d\vec{r}}{dt}\right) - r\frac{d\vec{r}}{dt}\right] \end{align}\]
Note:
$$ a \times (b \times c) = (a \cdot c)b - (a \cdot b)c\\ \Rightarrow \left(\hat{r} \cdot \frac{d\vec{r}}{dt}\right)\vec{r} - (\hat{r} \cdot \vec{r})\frac{d\vec{r}}{dt},\quad \vec{r} = r\hat{r}\\ \Rightarrow \left(\hat{r} \cdot \frac{d\vec{r}}{dt}\right)\vec{r} - r\frac{d\vec{r}}{dt} $$
$$ a \times (b \times c) = (a \cdot c)b - (a \cdot b)c\\ \Rightarrow \left(\hat{r} \cdot \frac{d\vec{r}}{dt}\right)\vec{r} - (\hat{r} \cdot \vec{r})\frac{d\vec{r}}{dt},\quad \vec{r} = r\hat{r}\\ \Rightarrow \left(\hat{r} \cdot \frac{d\vec{r}}{dt}\right)\vec{r} - r\frac{d\vec{r}}{dt} $$
看等號右邊
\[\begin{align} RHS &= -\frac{mk}{r^2} \left[r\hat{r}\hat{r} \cdot \frac{d(r\hat{r})}{dt} - r\frac{d}{dt}(r\hat{r})\right]\\ &= -\frac{mk}{r^2} \left[r\hat{r}\hat{r} \cdot \left(\frac{dr}{dt}\hat{r} + r\frac{d\hat{r}}{dt}\right) - r\left(\frac{dr}{dt}\hat{r} + r\frac{d\hat{r}}{dt}\right)\right]\\ &= -\frac{mk}{r^2} \left[r\hat{r} \left(\frac{dr}{dt} + r\hat{r} \cdot \frac{d\hat{r}}{dt}\right) - r\frac{dr}{dt}\hat{r} - r^2\frac{d\hat{r}}{dt}\right]\\ &=mk\frac{d\hat{r}}{dt} \end{align}\]只留下中括號中的第四項，因為一和三消掉，第二項則因為若$r$是固定的，$d\hat{r}\perp\hat{r}$。
接著看原本的等號左邊
\[LHS = \frac{d\vec{p}}{dt}\times\vec{L}=\frac{d(\vec{p}\times\vec{L})}{dt}\\ \left(\because\frac{d\vec{L}}{dt}=0\right)\]兩邊結合得到
\[\frac{d(\vec{p}\times\vec{L})}{dt} = mk\frac{d\hat{r}}{dt}\\ \Rightarrow \frac{d}{dt}(\vec{p}\times{\vec{L}}-mk\hat{r})=0\]括號內也是新的守恆量，我們稱其為 Laplace-Runge-Lenz Vector。
注意這個關鍵點在於受力必須是正比於$-\frac{\hat{r}}{r^2}$，消掉$r^2$才會獲得，所以必須要是牛頓重力場才有這個守恆量。
LRL Vector 意義
現在定
\[\vec{p}\times{\vec{L}}-mk\hat{r}\equiv\vec{c}\]方向
\[\begin{align} \because &\vec{L}\equiv \vec{r}\times\vec{p}\\ \Rightarrow &\vec{L}\cdot{\vec{c}}=0\\ \Rightarrow &\vec{L}\perp\vec{c} \end{align}\]代表$\vec{c}$的方向在軌道平面上，加上因為是守恆量，我們可以隨意選軌道的一點來看。方便起見，我們選近日點畫畫看
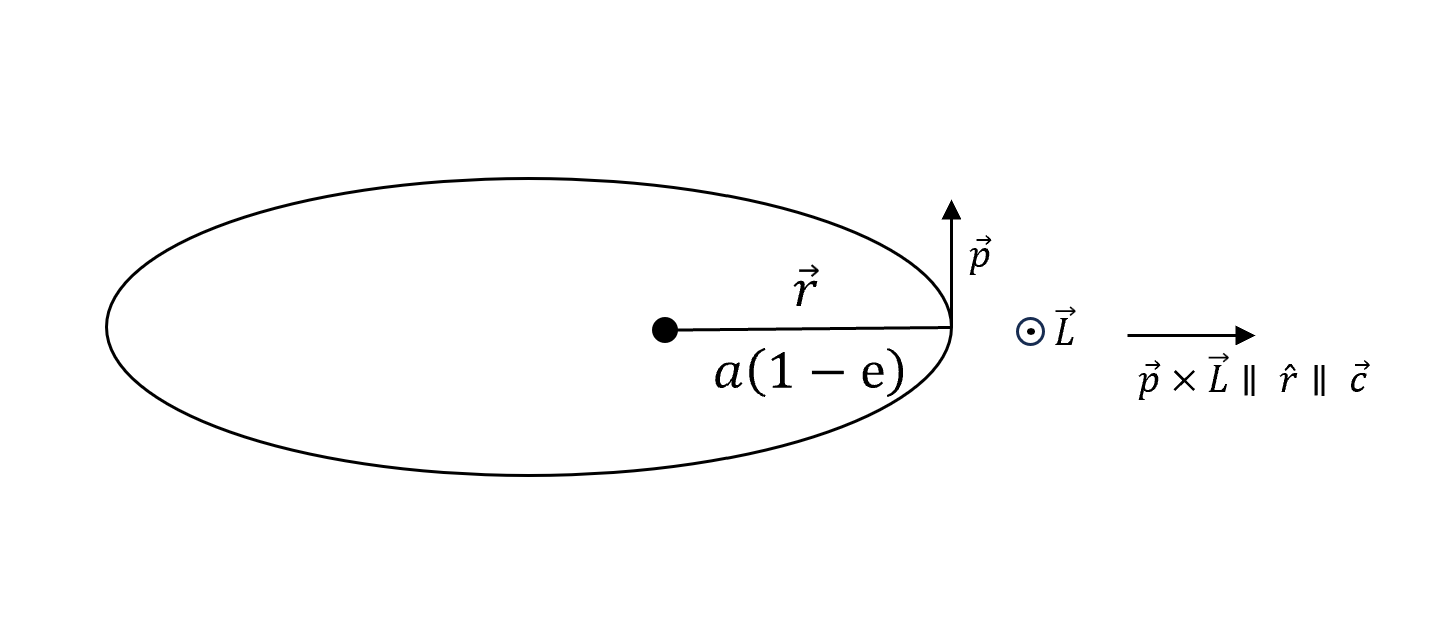
大小
\[\begin{align} \vec{c} \cdot \hat{r} &= (\vec{p} \times \vec{L}) \cdot \hat{r} - mk\\ &= (\hat{r} \times \vec{p}) \cdot \vec{L} - mk\\ &= \frac{1}{r} (\vec{r} \times \vec{p}) \cdot \vec{L} - mk\\ &= \frac{1}{r} (\vec{L}) \cdot \vec{L} - mk\\ &= \frac{L^2}{r} - mk\\ &= \frac{(mrv)^2}{r} - mk \\ &= \left(mv^2 - \frac{k}{r}\right)rm \\ &= (2KE-PE)rm\\ &= \left[\left(-\frac{k}{2a} - \left(-\frac{k}{r}\right)\right) \times 2 - \frac{k}{r}\right]mr\\ &\quad\left(\because KE+PE=E=-\frac{k}{2a},\quad KE=E-PE=-\frac{k}{2a}-\left(-\frac{k}{r}\right)\right)\\ &= \left(-\frac{k}{a} + \frac{k}{r}\right)mr\\ &= km\left(1 - \frac{r}{a}\right)\\ &= km\left(1 - \frac{a(1-e)}{a}\right)\\ &= kme \end{align}\]代表$\vec{c}$的大小和離心率有關。
確定軌道形狀
整理一下
\[\frac{\vec{p}\times\vec{L}}{mk}-\hat{r}=\frac{\vec{c}}{mk}=\frac{c\hat{c}}{mk}=\frac{kme\cdot\hat{c}}{mk}=e\hat{c}=e\cdot\hat{a}\]所以只要給定$\vec{r},\vec{p}$，確定$\vec{L}$，得到了軌道平面。
再用 Laplace-Runge-Lenze的組合 $\vec{p}\times\vec{L}-mk\hat{r}$，就可以決定離心率$e$，加上$\hat{a}$的指向，整個軌道形狀和指向就可以確定下來。
利用複變
前面在解這個問題的時候，是已知軌道是2D，所以一開始 EOM 拿過來，就在用向量的一些特性解出來。
但是其實我們可以更進一步用簡單的複變來解2D問題。
首先來看下2D座標，描述particle的位置
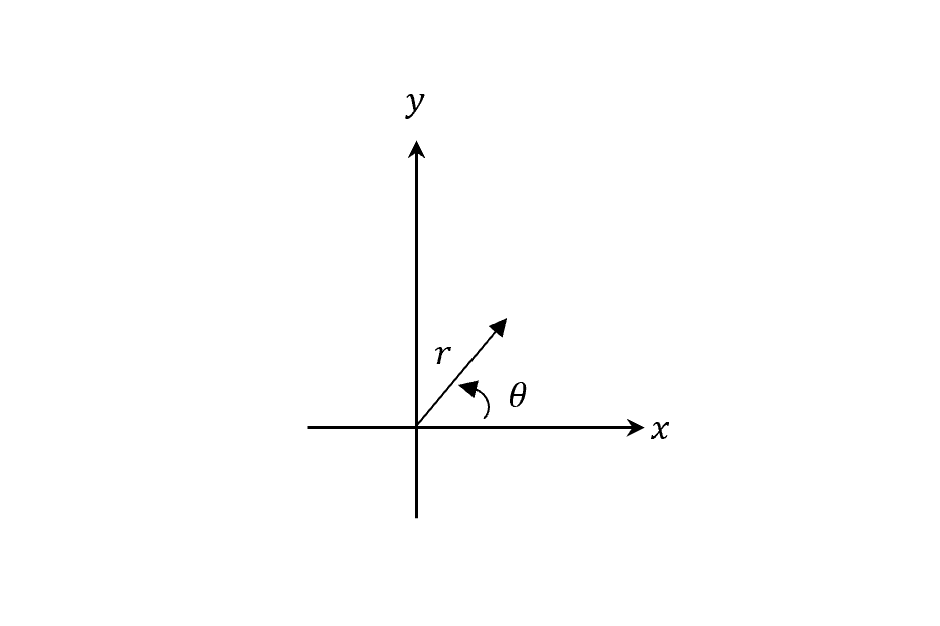
EOM
\[z\equiv re^{i\theta}=x+iy\Rightarrow\text{position vector}\\ m\frac{d\dot{z}}{dt}=-\frac{k}{r^2}e^{i\theta}\\ (e^{i\theta}\text{:unit direction of radial vector})\]
Note:
複習一下複變的基本運算
微分： $$ e^{i\theta}\frac{d\theta}{dt} = \frac{1}{i}\frac{de^{i\theta}}{dt} $$ 向量逆時針轉90度： $$ iz=ze^{i\frac{\pi}{2}} $$ 算距離： $$ |z-z_0|=r\\ (z_0\text{:center}, \quad z\text{:arbitraty}, \quad r\text{:radius}) $$
複習一下複變的基本運算
微分： $$ e^{i\theta}\frac{d\theta}{dt} = \frac{1}{i}\frac{de^{i\theta}}{dt} $$ 向量逆時針轉90度： $$ iz=ze^{i\frac{\pi}{2}} $$ 算距離： $$ |z-z_0|=r\\ (z_0\text{:center}, \quad z\text{:arbitraty}, \quad r\text{:radius}) $$
重新求得 LRL Vector 守恆
\[L = mr^2\frac{d\theta}{dt} \Rightarrow \frac{1}{r^2} = \frac{m}{L}\frac{d\theta}{dt}\]代進EOM
\[m\frac{d\dot{z}}{dt} = -ke^{i\theta}\cdot \frac{m}{L}\frac{d\theta}{dt}=-\frac{mk}{L}\frac{1}{i}\frac{de^{i\theta}}{dt}\\\]移項
\[\frac{d}{dt}(m\dot{z} - \frac{imk}{L}e^{i\theta}) = 0\\ m\dot{z} - \frac{imk}{L}e^{i\theta} = \text{constant vector}\\ \Rightarrow -im\dot{z}L - mke^{i\theta} = \text{constant}\]- 第一項：$\dot{z}$轉90度，畫個圖方向一樣就是$\vec{p}\times\vec{L}$。
- 第二項：因為我們定$e^{i\theta}$就是$\hat{r}$，所以這項其實就是$mk\hat{r}$。
而且跟我們之前推的LRL公式一樣！
\[-im\dot{z}L - mke^{i\theta}\\ =\vec{p}\times{\vec{L}}-mk\hat{r}\]方向
按照前述把
\[-im\dot{z}L - mke^{i\theta}\]畫出來
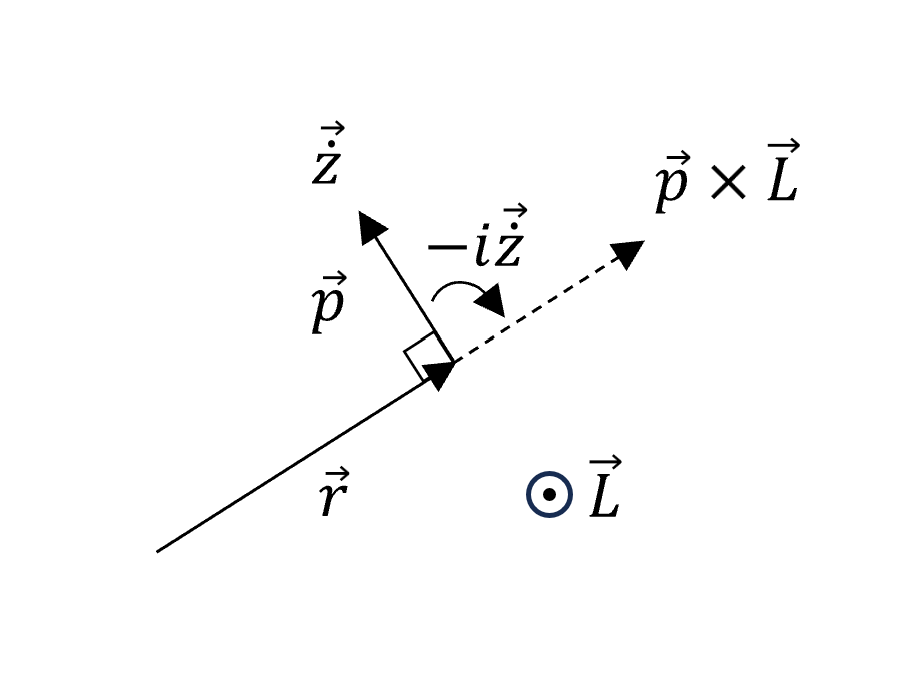
Momentum Space 的軌道形狀
回到一開始複變求出來的公式
\[m\dot{z} - \frac{imk}{L}e^{i\theta} = \text{constant vector}\]簡化一下
\[\Rightarrow p-i\frac{mk}{L}e^{i\theta}\equiv D\]移項算長度
\[\bigg|\bigg|\vec{p}-\vec{D}\bigg|\bigg|=\bigg|\frac{imk}{L}e^{i\theta}\bigg|=\frac{mk}{L}\]按照複變的特性，這就表示是一個circle！
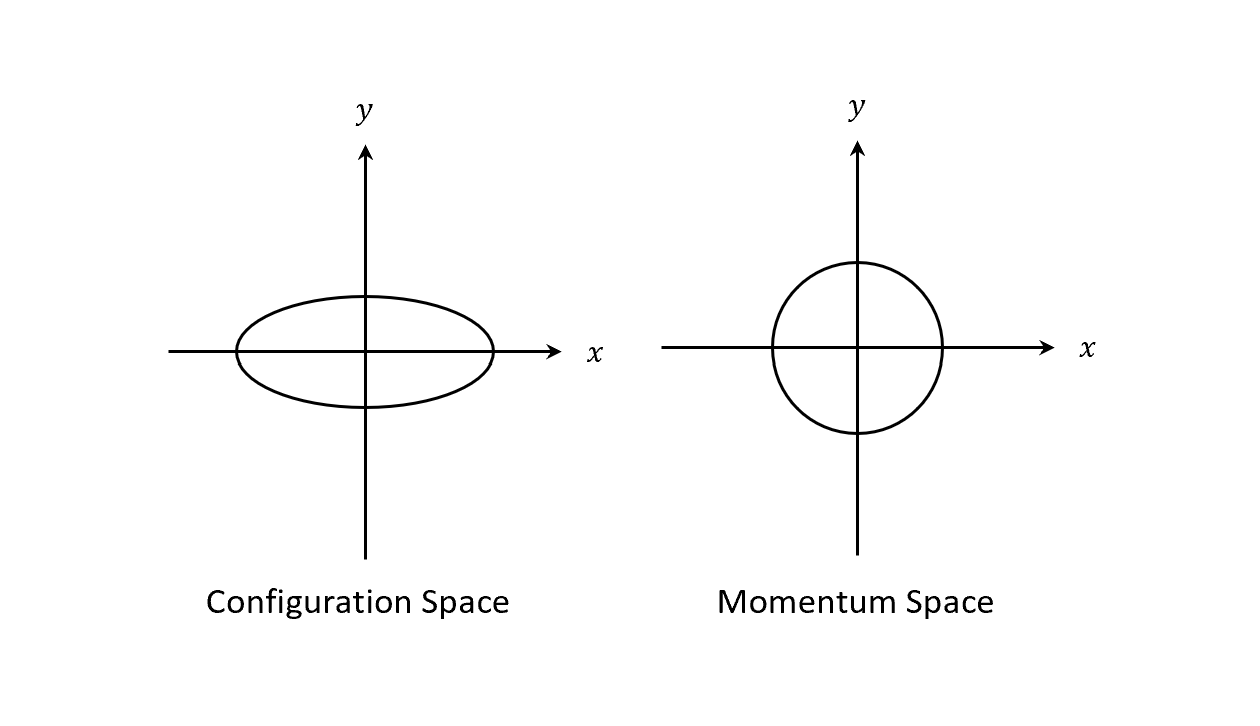
總結軌道形狀
在不同space下
- Configuration Space: Ellipse
- Momentum Space: Circle
(題外話，早期古人形容橢圓軌道，都是用大圓圈加小圓圈(快慢)來組成，背後隱藏的精神其實是Fourier series，有低頻高頻的解，所以是把一個圓形軌道加一點擾動的感覺，去弄成和觀測結果相近的結果)