(7) 軌道 Newton ─ Gravitational Field 橢圓軌道形狀、週期與位置
一樣從第一節描述軌道形狀的軌道公式
\[\frac{d^2u}{d\theta^2} + u = J(u), \quad J(u) = -\frac{m}{l^2}\frac{dV}{du}, \quad u \equiv \frac{1}{r}\]位能代重力場算算看。
重力場位能代入軌道方程解
知道重力場位能
\[V = -\frac{k}{r} = -ku,\quad k = mMG\]代入軌道公式為
\[\frac{d^2u}{d\theta^2} + u = \frac{mk}{l^2}\]直接解
\[\begin{align} \Rightarrow u &= \frac{mk}{l^2} + B\cos\theta, \quad B: \text{some constant}\\ \Rightarrow r &= \frac{1}{u} \\ &= \frac{1}{\frac{mk}{l^2} + B\cos\theta} \\ &= \frac{(l^2/mk)}{1 + \frac{Bl^2}{mk}\cos\theta} \\ &\equiv \frac{A}{1+e\cos\theta} \end{align}\]其中
\[\begin{cases} A \equiv \frac{l^2}{mk}\\ e \equiv \frac{Bl^2}{mk} \equiv \text{eccentricity of ellipse} \quad -(4) \end{cases}\]畫出圖
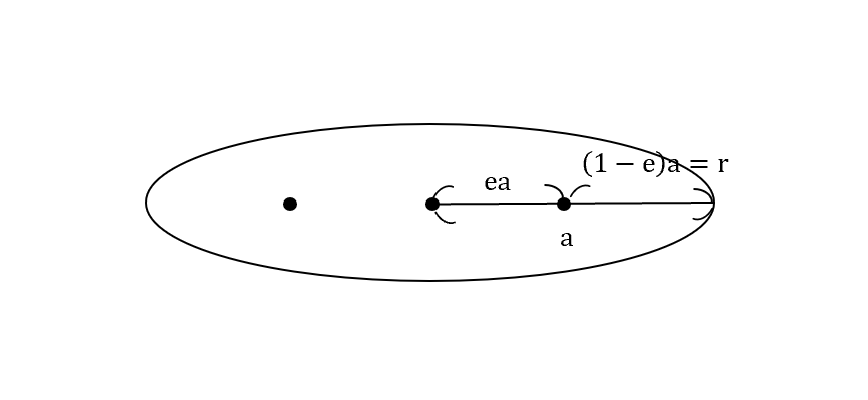
若$\theta=0$
\[(1-e)a=\frac{A}{1+e}\\ \Rightarrow A=(1-e^2)a\]代進$r$
\[r = \frac{(1-e^2)a}{1+e\cos\theta}\]可以看到(4)式是幾何特性,而$A$原本的定義是物理特性(和角動量有關),所以當把$A$的等式合併
\[(1-e^2)a = \frac{l^2}{mk}\quad -(5)\]等號左邊的$e,a$都是幾何,右邊是物理特性。
能量守恆計算$B$
接下來繼續求$B$。
一樣能量守恆(negative engergy for a bound elliptical orbit)
\[\frac{m}{2}\left(\frac{dr}{dt}\right)^2 + \frac{m}{2}r^2\left(\frac{d\theta}{dt}\right)^2 - \frac{k}{r} = E\]加上角動量守恆
\[l \equiv mr^2\frac{d\theta}{dt} = \text{conserved}\]代進去
\[\begin{align} \Rightarrow E &= \left(\frac{m}{2}\left(\frac{dr}{d\theta}\right)^2 + \frac{m}{2}r^2\right)\left(\frac{d\theta}{dt}\right)^2 - \frac{k}{r}\\ &= \frac{m}{2}\left(\left(\frac{dr}{d\theta}\right)^2 + r^2\right)\left(\frac{l}{mr^2}\right)^2 - \frac{k}{r} \end{align}\]若是把我們前面的$r$代進來,會太難解。
從special case $\theta=0$ 出發。
前面求到
\[r = \frac{(1-e^2)a}{1+e\cos\theta}\]$\theta=0$代進去
\[r = \frac{(1-e^2)a}{1+e}\](即便這邊有疑慮覺得角度的變數沒了,但反正能量守恆,且和角度無關)
令極小值
\[\frac{dr}{d\theta} \to 0\]所以能量公式
\[\begin{align} \Rightarrow E &= \frac{m}{2}\frac{l^2}{m^2}\left(\frac{1+e}{(1-e^2)a}\right)^2 - k\frac{1+e}{(1-e^2)a}\\ &= \frac{l^2}{2m}\frac{1}{(1-e)^2}\frac{1}{a^2} - \frac{k}{(1-e)a} \end{align}\]把(5)式代進來替換$l$
\[\begin{align} \Rightarrow E &= \frac{1}{2}\frac{1}{(1-e)^2}\frac{1}{a^2}k(1-e^2)a - \frac{k}{(1-e)a}\\ &= \frac{k}{a}\left(\frac{1}{2}\frac{1+e}{1-e} - \frac{1}{1-e}\right) = \frac{k}{a}\frac{1}{1-e}\left(\frac{1+e}{2} - 1\right) = -\frac{k}{2a} \end{align}\]整理一下目前化簡的公式
\[\begin{align} E&=-\frac{k}{2a}\\ (1-e^2)a &= \frac{l^2}{mk}\\ e&=\frac{Bl^2}{mk}=B(1-e^2)a \end{align}\]求出$B$
\[\Rightarrow B = \frac{e}{1-e^2}\frac{1}{a}\]離心率(幾何)和能量(物理)性質連結關係
最後來連結 $E$ 和 $e$ 的關係
\[1-e^2=\frac{l^2}{mk}\frac{1}{a}=\frac{l^2}{mk}\frac{2|E|}{k}\\ \Rightarrow e=\sqrt{1-\frac{2l^2|E|}{mk}}\]可以看到描述幾何形狀的$e$和物理性質的角動量$l,E$有關!
用角動量守恆求軌道週期
現在來算一下軌道週期,我們直接從角動量守恆出發
\[mr^2\frac{d\theta}{dt} \equiv l = \text{constant}\]軌道解
\[r = \frac{a(1-e^2)}{1+e\cos\theta}\]做時間積分
\[T = \int_0^T dt = \frac{m}{l}\int_0^{2\pi} \frac{a^2(1-e^2)^2}{(1+e\cos\theta)^2} d\theta\]用微積分繼續做下去可以解,但其實挺複雜的,我們來看比較簡單的幾何方式。
幾何方式求週期 (克普勒第三運動定律)
先來看簡單的數學幾何
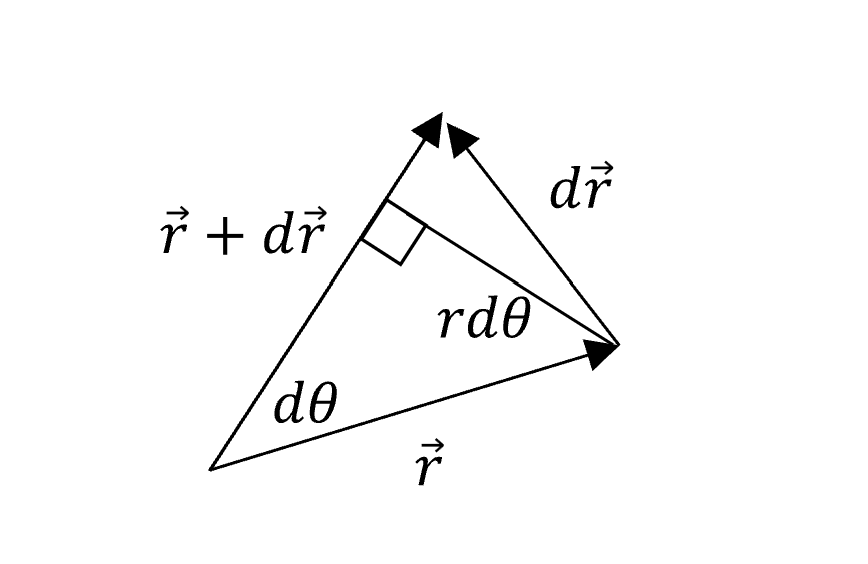
由上圖可見,掃過的小面積。
\[\frac{r\cdot r d\theta}{2}\]所以角動量守恆下的時間積分可以表示為
\[\begin{align} \int dt &= \frac{m}{l}\int r^2 d\theta\\ &= \frac{2m}{l}\int \frac{r^2}{2} d\theta\\ &= \frac{2m}{l} \cdot (\text{total area of the orbit})\\ &=\frac{2m}{l} \cdot \pi \cdot a \cdot b\\ \end{align}\\ (b: \text{semi-minor axis},\quad a: \text{semi-major axis})\]求得週期
\[T = \frac{2\pi m}{l} a \cdot b = \frac{2\pi m}{l} a^2\sqrt{1-e^2}\]又之前知道
\[r = \frac{a(1-e^2)}{1+e\cos\theta}\\ a(1-e^2) = \frac{l^2}{mk}\]代進去得
\[\Rightarrow T = 2\pi m a^2 \sqrt{\frac{l^2}{mka}} = 2\pi \sqrt{\frac{m}{k}} a^{\frac{3}{2}}\]得證克普勒的第三運動定律!
\[T \propto a^{\frac{3}{2}}\]計算特定時間點的位置
現在來問,若給定時間 t,那麼 planet 的位置會在哪裡呢?
等於是我們要算
\[t = \int_0^t dt = \frac{m}{l} \int_0^{\theta} \frac{a^2(1-e^2)^2}{(1+e\cos\theta)^2} d\theta = f(\theta)\]可是微積分做完之後,還要 invert 回去算
\[\theta = \theta(t)\]感覺很複雜,我們一樣用克普勒幾何的方式來解。
克普勒幾何方式求點位置 (克普勒方程)
克普勒第二運動定律知道每單位時間掃過的面積是一樣的,所以知道時間就等於知道面積,但是要算橢圓面積還是很難的,因此我們額外畫一個輔助圓,可以想像橢圓其實是圓形壓縮來的。
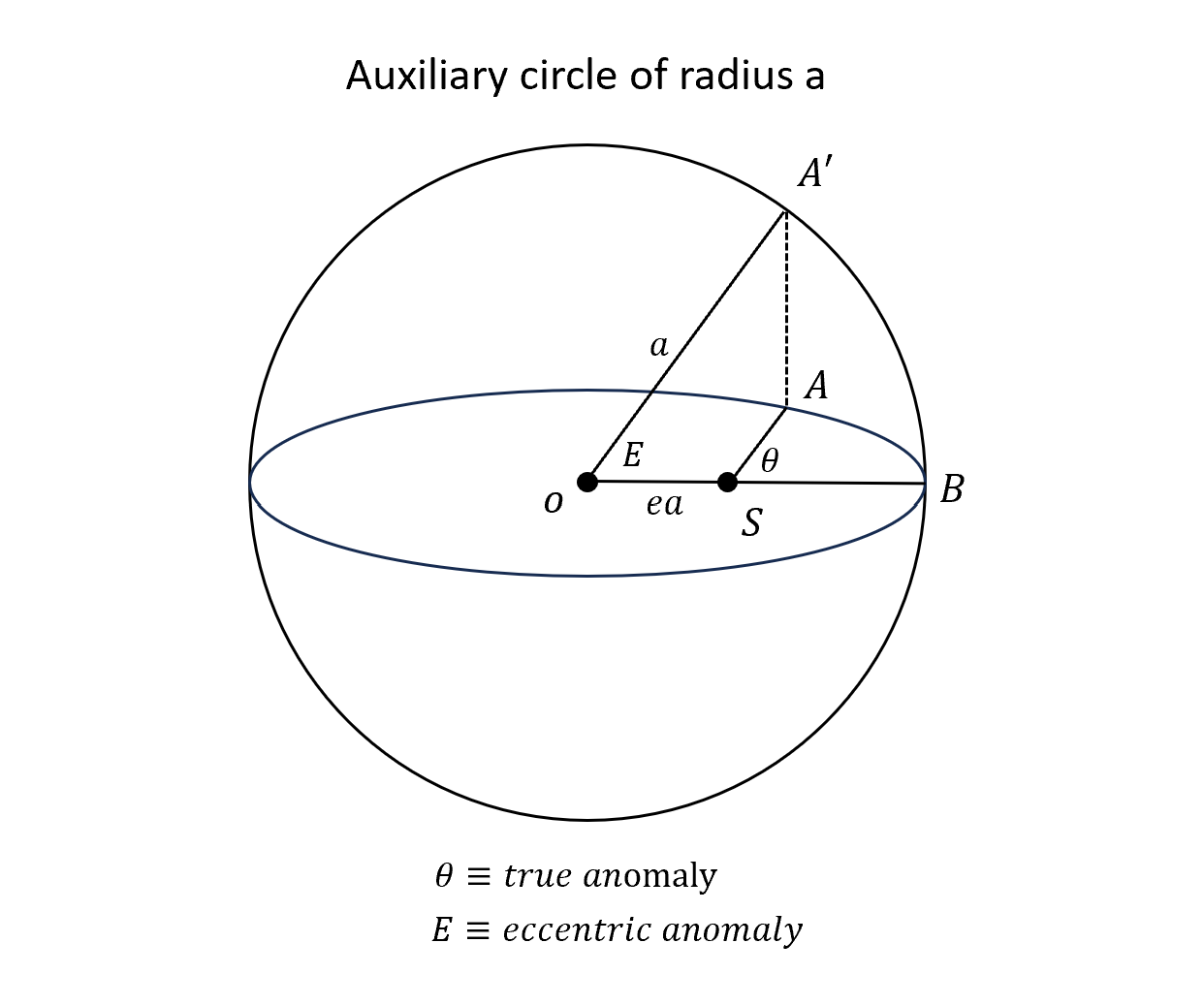
舉例一般橢圓方程
\[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\]壓縮的半短軸和面積
\[\begin{align} b =& a \Rightarrow \text{circle}\\ b =& a\sqrt{1-e^2} \Rightarrow\text{ellipse} \\ & (\text{ compress by a factor of }\sqrt{1-e^2})\\ \text{area}(SAB) =& \text{area}(SA'B) \cdot \sqrt{1-e^2} \end{align}\]
所以用面積表示掃過時間比
移項
\[\begin{align} \text{area}(SA'B) &= \pi a^2 \frac{t}{T}\\ &= \text{area}(OA'B) - \text{area}(OA'S)\\ &= \frac{Ea^2}{2} - \frac{(a\sin E) \cdot ea}{2} \end{align}\]得到所謂的克普勒方程(Kepler’s equation)
\[2\pi \frac{t}{T} = E - e\sin E = M\text{ mean anomaly}\]所以當週期 $T$ 已知,給定時間 $t$ 和 $M$,算 $E$ 對應的 $\theta$ 就會是最終位置。
Eccentricity Anomaly 和 $\theta$ 關係
看幾何圖
\[a\cos E - ea = r\cos \theta = \frac{a(1-e^2)}{1+e\cos \theta} \cos \theta\]整理
\[\begin{align} (1+e\cos \theta) (\cos E - e) &= (1-e^2) \cos \theta\\ (\cos E - e) + (e\cos \theta \cos E - e^2 \cos \theta) &= (1-e^2) \cos \theta\\ \cos E - e &= (1-e^2 - e\cos E + e^2) \cos \theta\\ &= (1-e\cos E) \cos \theta \end{align}\]得最後關係式
\[\cos \theta = \frac{\cos E - e}{1 - e\cos E}\]所以接下來重點就是要求$E$了!
求 Eccentricity Anomaly
數值解
設$M$已知
\[M = E - e\sin E\]若$e$很小,用迭代解,舉個例子
\[\begin{align} 0.5x^2 + x - 2 &= 0\\ x &= 2 - 0.5x^2\\ x^{(0)} &= 2\\ x^{(1)} &= 2 - 0.5 {x^{(0)}}^2\\ &\vdots \end{align}\]同理
\[\begin{align} E &= M + e\sin E\\ E^{(0)} &= M \quad (\text{e 很小,先扔了})\\ E^{(1)} &= M + e\sin E^{(0)}\\ E^{(2)} &= M + e\sin E^{(1)}\\ &\vdots \end{align}\]繼續求到收斂就好。
解析解 (Bessel Observation)
但除此之外,還有別的作法。
之前圖和公式可以看到,若每次$M$回來,$E$也會$2\pi$回來,所以可以將$E-M$視為$M$的週期函式(代表$M$加$2\pi$後,$E-M$的結果不變)
\[\begin{align} M &= E - e\sin E\\ M' &\equiv M+2\pi\\ M' &= E'- e\sin E'\\ \text{if } E' &= E+2\pi\\ M' &= (E+2\pi)- e\sin (E+2\pi)\\ M' &= (E+2\pi)- e\sin (E)\\ E' - M' &= (E+2\pi) - (M+2\pi) = E-M = e\sin(E) \end{align}\]既然是跟週期有關,那直覺就是 Fourier Series 展開
\[E - M = e\sin E = \sum_{n=1}^{\infty} C_n \sin(nM)\]求係數
\[\int_0^{2\pi} e\sin E \sin(nM) dM = C_n \int_0^{2\pi} \sin^2(nM) dM = C_n \pi\] \[\begin{align} C_n &= \frac{e}{\pi} \int_0^{2\pi} \sin E \sin(nM) dM\\ &= \frac{e}{\pi} \int_0^{2\pi} \frac{\sin E}{n} (-d\cos(nM))\\ &= \frac{1}{n\pi} \int \cos(nM) \cdot d(e\sin E)\\ &= \frac{1}{n\pi} \int \cos(nM) (dE - dM)\\ &= \frac{1}{n\pi} \int \cos(nM) dE \end{align}\]整理
\[M = E - e\sin E\\ \begin{align} C_n &= \frac{1}{n\pi} \int \cos(n(E-e\sin E)) dE\\ &= \frac{1}{n\pi} \int \cos(nE - ne\sin E) dE \end{align}\]而 Bessel function 的積分形式
\[J_\nu(x) \propto \int_0^{2\pi} \cos(\nu\theta - x\sin\theta) d\theta \quad , \nu = \text{integer}\]對照一下我們的 $C_n$就是 $J_n(ne)$。
這樣的好處就是,因為$J_\nu(x)$會decay的很快,所以只要取前幾項就可以了,只要$C_n$只要找前幾項之後,加上$M$已知,所以就能得到$E$,可以算是種解析解。
