(9) 軌道 Bohlin Transformation ─ Mapping Hooke to Newton

前言

從第五節和第七節知道 Hooke’s SHO 和 Newton’s Gravitational field 求出的軌道都是橢圓形狀，我們現在要進一步來看這兩者之間的關係，用 Bohlin Transformation 把 Hooke Mapping 到 Newton 上。

我們將會看到Hooke 和 Newton 對應的同一件事情。

虎克橢圓軌道公式變換

已知 2D SHO 橢圓軌道

\[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\]

SHO是從原點開始算

\[\begin{cases} x = r\cos\theta\\ y = r\sin\theta \end{cases}\]

得

\[r^2 = \frac{1}{\frac{\cos^2\theta}{a^2} + \frac{\sin^2\ theta}{b^2}}\]

替換

\[\begin{cases} \sin^2\theta = \frac{1-\cos2\theta}{2}\\ \cos^2\theta = \frac{1+\cos2\theta}{2} \end{cases}\]

化簡

\[\begin{align} \Rightarrow r^2 &= \frac{2}{\frac{1+\cos2\theta}{a^2} + \frac{1-\cos2\theta}{b^2}}\\ & = \frac{2}{(\frac{1}{a^2}+\frac{1}{b^2}) - (\frac{1}{b^2}-\frac{1}{a^2})\cos2\theta}\\ &= \frac{2/(\frac{1}{a^2}+\frac{1}{b^2})}{1 - \frac{\frac{1}{b^2}-\frac{1}{a^2}}{\frac{1}{b^2}+\frac{1}{a^2}}\cos2\theta}\\ \end{align}\]

現令

\[\begin{cases} R = r^2 \\ \theta' = 2\theta\\ e' = \frac{a^2-b^2}{a^2+b^2} = \frac{\frac{1}{b^2}-\frac{1}{a^2}}{\frac{1}{b^2}+\frac{1}{a^2}}\\ a' = \frac{a^2+b^2}{2} \end{cases}\]

代進去得

\[R = \frac{a'(1-e'^2)}{1-e'\cos\theta'}\\\]

現在我們把 $(R, \theta’)$ 當作是一組新的座標來表示虎克的橢圓軌道。

(這邊注意一下，分母是減號，所以算的$R$是從遠日點開始算。)

複變 with Bohlin Transformation

複變有很好的數學性質，平方後長度平方、角度也變成兩倍，跟我們前面在做的變換是一樣的

\[\begin{cases} R = r^2 \\ \theta' = 2\theta\\ \end{cases}\]

所以現令

• 原本起自原點的軌道座標為$(r,\theta)$，在$\mathscr{z}$平面。
• 變換後起自遠日點的軌道座標為$(R, \theta’)$，在$\mathcal{Z}$平面。

數學意思就是

\[z\equiv x+iy\equiv re^{i\theta}\\ \mathcal{Z}\equiv{z}^2=r^2e^{i2\theta}\equiv R e^{i\theta'}\]

畫個圖

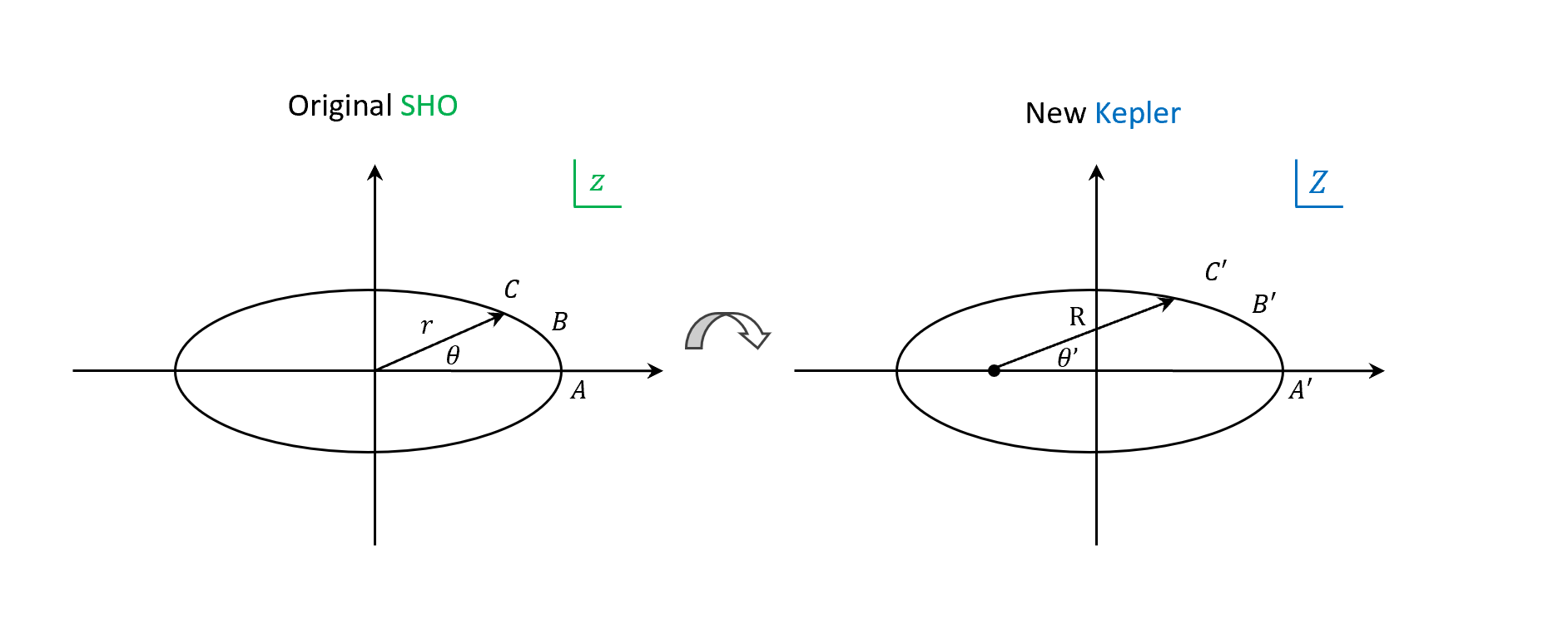
其中我們做

\[\mathcal{Z}\equiv{z}^2\]

就是 Bohlin Transformation。

SHO Map to Kepler Mapping

現在 Mapping 完，只有確認對應橢圓形狀相同，其他物理性質可能不同

• 距離起點從原點變成遠日點
• 因為角度兩倍，SHO走一半，Kepler已經走完一圈
• $ABC$若是等時間單位，不代表對應的$A’B’C’$也是，需要重新計算時間點的對應關係。

找對應時間點

設

• 原本SHO的時間：t
• Mapping後的 Kepler 時間：T

現在要找物體在SHO運動的時間t，對應Kepler的時間是多少，所以我們要求

\[T(t)\]

的公式。

角動量守恆出發

Mapping 後其實也沒有保證角動量會持續守恆，但為了 Mapping 是到 Kepler 軌道，Kepler 有角動量守恆，所以我們用這個前提去推導$T(t)$，知道每個瞬間怎麼走就會知道吸引力長什麼樣子。

但還有一點的是，我們是想要找虎克和牛頓之間的關係，但角動量守恆沒有保證一定是$1/r^2$的力，只有保證是 central field with rotational symmetry。

只是後見之明知道，牛頓已經證出如果軌道是圓錐曲線，那麼 rotationally symmtric central attractive force 一定是$1/r^2$。

所以接下來就放心用角動量守恆吧！

計算$T(t)$公式

設原本SHO軌道的角動量為

\[r^2\frac{d\theta}{dt}\equiv l \equiv \text{ constant angular momentem}\]

Map 完的Kepler角動量為

\[R^2\frac{d\theta'}{dT}\equiv L\]

現在$L$要維持守恆，所以

\[R^2\frac{d\theta'}{dT}\\ =(r^2)^2 \frac{d(2\theta)}{dT}\\ = 2r^4 \frac{d\theta}{dt} \frac{dt}{dT}\\ = L = \text{const}\]

代入$l$

\[L = 2r^2 l\frac{dt}{dT} \\ \Rightarrow dT = \frac{2l}{L}r^2 dt \equiv (\alpha) r^2 dt\\ (\alpha\text{: some constant for a given orbit})\]

原本SHO軌道

\[\begin{cases} x = r\cos\theta\\ y = r\sin\theta \end{cases}\]

時間$t=0$我們選簡單的，起始在$x$軸上的點，所以

\[\frac{d^2\vec{r}}{dt^2}=-\omega^2\vec{r}\Rightarrow\frac{d^2\vec{r}}{dt^2}=-\vec{r}\]

(Rescale一下，時間沒因次，$\omega$變成1)

所以

\[dT = \alpha (a^2\cos^2t + b^2\sin^2t) dt\\ T = \alpha \int_0^t (a^2\cos^2t + b^2\sin^2t) dt \Rightarrow T = T(t)\]

到此，先不算積分，就已經可以代進去算Map完的EOM，找Map完後是受什麼力，直接跳下面部分看答案。

繼續算

\[\begin{align} T &= \alpha \int_0^t (a^2\cos^2t + b^2\sin^2t) dt\\ &= \alpha \int_0^t \left(a^2 \frac{1+\cos 2t}{2} + b^2 \frac{1-\cos 2t}{2}\right) dt\\ &= \alpha \left(\frac{a^2+b^2}{2} t + \frac{a^2-b^2}{2} \int \cos 2t dt\right)\\ &= \alpha \left(\frac{a^2+b^2}{2} t + \frac{a^2-b^2}{4} \sin 2t\right)\\ &= \frac{\alpha}{4} (a^2+b^2) \left(2t + \frac{a^2-b^2}{a^2+b^2} \sin 2t\right) \end{align}\]

這個延伸的意義我們會到下一個章節再提。

找對應的EOM和力

Map完的EOM

\[\begin{align} \frac{d^2\mathcal{Z}}{dT^2}&=\frac{d}{dT}\left(\frac{d\mathcal{Z}}{dT}\right)=\frac{dt}{dT}\frac{d}{dt}\left(\frac{dt}{dT}\frac{d\mathcal{Z}}{dt}\right)\\ &= \frac{1}{\alpha r^2} \frac{d}{dt} \left(\frac{1}{\alpha r^2} \frac{d\mathcal{Z}}{dt}\right) \\ &= \frac{1}{\alpha^2} \frac{1}{zz^*} \frac{d}{dt} \left(\frac{1}{zz^*} \frac{dz^2}{dt}\right)\\ &= \frac{2}{\alpha^2} \frac{1}{zz^*}\frac{d}{dt}\left(\frac{1}{z^*}\frac{dz}{dt}\right)\\ &=\frac{2}{\alpha^2}\frac{1}{zz^*}\frac{z^*\frac{d^2z}{dt^2}-\frac{dz}{dt}\frac{dz^*}{dt}}{z^{*^2}}\\ &=\frac{2}{\alpha^2}\frac{1}{zz^{*^3}}\left(z^*(-z)-\frac{dz}{dt}\frac{dz^*}{dt}\right)\\ &\quad(\because \frac{d^2 z}{dt^2}=-z\text{ for the original SHO})\\ &=-\frac{2}{\alpha}\frac{1}{zz^{*^3}}(2\epsilon)\\ &\quad(\epsilon \equiv \text{ total energy of the original SHO})\\ &=-\frac{4\epsilon}{\alpha^2}\frac{z^2}{(zz^*)^3} \end{align}\]

來來來，看看我們得到了什麼！

\[\frac{d^2\mathcal{Z}}{dT^2} = -\frac{4\epsilon}{\alpha^2}\frac{z^2}{(zz^*)^3} = -\frac{4\epsilon}{\alpha^2}\frac{\mathcal{Z}}{|\mathcal{Z}|^3}\]

把

\[\frac{4\epsilon}{\alpha^2}\equiv GM\equiv\frac{k}{m}\\ \alpha = \sqrt{\frac{4\epsilon}{GM}}\]

這不就是牛頓的萬有引力嗎！

虎克與牛頓是同件事

至此，虎克做Bohlin Transformation後，對應的就是受到牛頓萬有引力的克普勒軌道運動！

(所以SHO走的$A\to B \to C$可能都是1秒，對到Kepler運動後$A’\to B’ \to C’$可能是1秒、1.3秒、1.5秒。)