(2) 熱力 ─ 熱平衡
熱平衡是怎麼達成的?
現在有兩個系統,一大一小
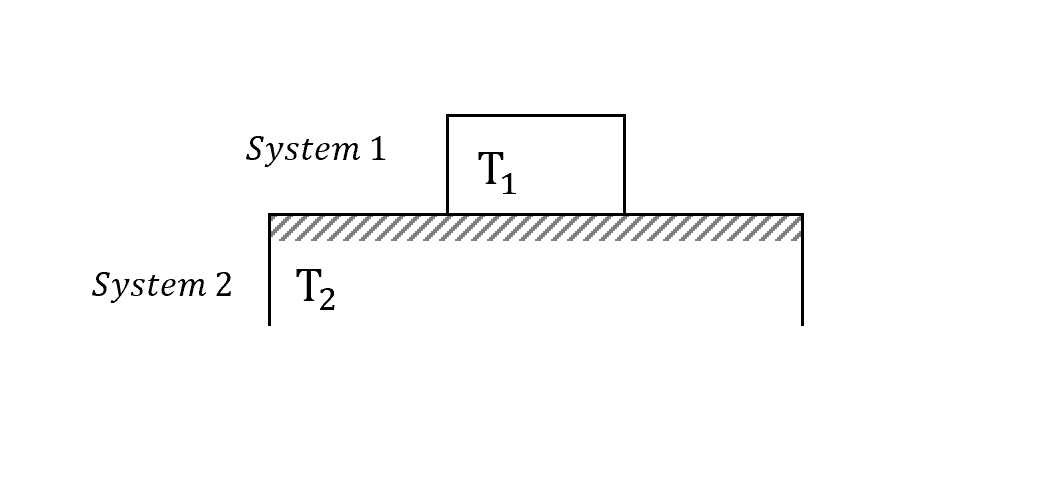
假設
\[T_2>T_1 (\Delta T \text{ is small})\]並且系統二很大,是個穩定熱庫,溫度不太會變化,那麼系統一的溫度隨時間會怎麼改變?
常識直覺應該就是長這樣
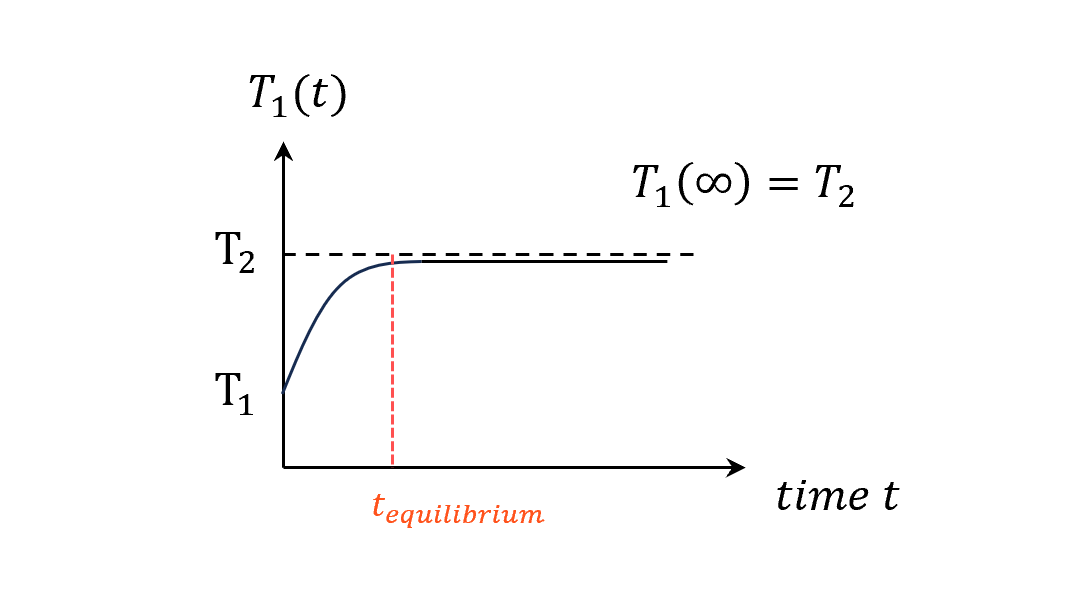
會有一個達成熱平衡(系統一溫度等於系統二溫度)的時間。
到這裡都很正常吧,我們把一顆球丟到超大盆熱水中,那顆球的溫度就會漸漸地跟水一樣。
但這樣了解的還不夠,從這裡我們只能知道當我們稱兩個系統達成熱平衡的時候溫度一樣,但溫度是什麼?究竟是什麼物理量達到一樣?又為什麼會達到一樣呢?
熱平衡時相等的物理量是什麼?
現在用一個簡單的模型來看微觀上的碰撞(microscopic collisions),兩個系統中的氣體分子發生碰撞進行能量交換。
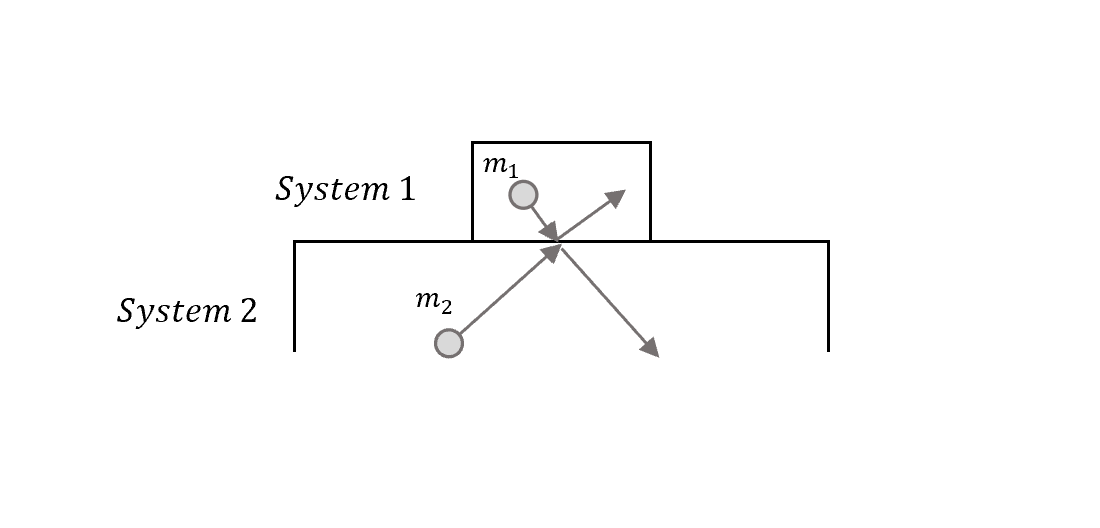
假設現在在一維,牛頓的動量守恆(彈性碰撞)告訴我們,碰撞後的速度
\[v_1'=\frac{m_1-m_2}{m_1+m_2}v_1+\frac{2m_2}{m_1+m_2}v_2\]所以系統一氣體分子在碰撞完之後的能量改變是
\[\Delta u_1=\frac{1}{2}m_1v_1'^2-\frac{1}{2}m_1v_1^2\\ =\frac{4m_1m_2}{(m_1+m_2)^2}\left[\frac{1}{2}m_2v_2^2-\frac{1}{2}m_1v_1^2+\frac{1}{2}(m_1-m_2)v_1v_2\right]\]又因每次碰撞能量的改變有正有負,所以我們取個平均來看
\[\langle \Delta u_1 \rangle = \frac{4m_1m_2}{(m_1+m_2)^2}\left[\Bigg\langle\frac{1}{2}m_2v_2^2\Bigg\rangle-\Bigg\langle\frac{1}{2}m_1v_1^2\Bigg\rangle\right]\]其中cross term沒了,因為這兩個系統彼此互相獨立,從統計上我們知道兩個獨立事件的平均值等於兩個相乘,那分開相乘各自有正有負,所以等於0。
\[\langle v_1 v_2 \rangle = \langle v_1 \rangle \langle v_2 \rangle = 0\]接著,重點來了,在兩個系統達成熱平衡的時後,藉由碰撞的能量交換平均起來會是0,所以數學上來說就是,當達到熱平衡時,我們預期
\[\langle \Delta u_1 \rangle = 0\]進而得出
\[\Rightarrow \Bigg\langle\frac{1}{2}m_2v_2^2\Bigg\rangle = \Bigg\langle\frac{1}{2}m_1v_1^2\Bigg\rangle\]代表的意思就是,當這兩個系統沒有互相推擠、體積沒有改變、巨觀上沒有具體的改變,只有在微觀上(碰撞)的能量交換時,達到熱平衡的意思就是每一個氣體分子的平均動能相等!
然後我們進一步定義($k$是波茲曼常數):
\[\Bigg\langle\frac{1}{2}m_1v_1^2\Bigg\rangle \equiv \frac{1}{2}k T_1\\ \Bigg\langle\frac{1}{2}m_2v_2^2\Bigg\rangle \equiv \frac{1}{2}k T_2\\\]這兩個相等就代表
\[T_1 = T_2\]很驚人吧!從單純的牛頓動量守恆出發就可以得出這個結果,至此我們稍微整理一下。
小結
- 原本不同的兩個系統,碰撞完達到熱平衡的時候,指的是這兩個系統中每個分子的平均動能相等,也就是最前面提到的熱平衡時會相等的物理量。
- 平均動能我們就定義為溫度,溫度是個指標,每個系統有自己的溫度,熱平衡的時候兩個系統溫度一樣。
- 平均動能相等在這裡是用簡單的彈性碰撞模型推導出來。當然達成熱平衡的方式有非常多種,並非一定要是碰撞,但這是其中一個可以了解的最簡單方式,其他都只是推廣和變形而已。
平均動能與溫度差的關係
從前面的公式,我們把溫度代回去得到
\[\langle \Delta u_1 \rangle = \frac{4m_1m_2}{(m_1+m_2)^2}(T_2-T_1)\frac{1}{2}k\]中間那些都是常數,所以可以得到關係式
\[\langle \Delta u_1 \rangle \propto (T_2-T_1)\]以下討論三種狀況的溫度差
\[\begin{cases} T_2 > T_1\rightarrow \langle \Delta u_1 \rangle > 0\text{ (系統一得到能量,給的方式叫Q(Heat))}\\ T_1 > T_2\rightarrow \langle \Delta u_1 \rangle < 0\text{ (熱流反過來給系統二)}\\ T_2 = T_1\rightarrow \langle \Delta u_1 \rangle = 0\text{ (達到熱平衡)} \end{cases}\]可以看到溫度差和熱流的方向是有絕對性的關係,這也是我們平常更直覺的解釋方式
熱從高溫往低溫流!
實際計算系統溫度變化
那我們現在假設是第一個狀況,\(T_2 > T_1\),並且系統二很穩定,\(T_2\)為常數,求解\(T_1(t)\)。
首先一樣我們從兩個角度出發
1. 系統能量改變和溫差成正比
因為
\[\langle \Delta u_1 \rangle \propto (T_2-T_1)\]那麼單位時間能量的變化,就會和時間內發生幾次碰撞和每次碰撞時的能量變化有關係,所以得
\[\Bigg\langle \frac{du_1}{dt} \Bigg\rangle=f_\text{colli}\cdot \langle \Delta u_1 \rangle \propto (T_2-T_1)\]這裡一樣假設溫差不會太大,碰撞頻率趨近於常數。
2. 系統能量和溫度的變化
因為
\[\langle \Delta u_1 \rangle = \Bigg\langle\frac{1}{2}m_1v_1^2\Bigg\rangle = \frac{1}{2}k T_1\]那麼看單位時間能量的變化一樣得
\[\Bigg\langle \frac{du_1}{dt} \Bigg\rangle \propto \frac{dT_1}{dt}\]結合
結合兩個角度得到微分方程
\[\frac{dT_1(t)}{dt}=\gamma(T_2-T_1(t))\]其中$\gamma$因次是[1/time],接著我們就可以繼續求解$T_1(t)$囉!
定
\[x(t)\equiv T_1(t) - T_2\\ \Rightarrow \frac{dx}{dt}=\frac{dT_1}{dt}=-\gamma x\\ x(t)=x(0)e^{-\gamma t}=(T_1(0)-T_2)e^{-\gamma t}\\ T_1(t)=T_2+x(t)=T_2-(T_2-T_1(0))e^{-\gamma t}\]驗證一下得到這張圖

可以看到達到熱平衡的時間在溫差沒有太大的情況下都是一樣的,也就是說代表假設現在有一鍋100度$T_2$的水,你丟99度、98.5度的鐵球,達到熱平衡的時間都是一樣的!
