(9) 熱力 ─ Thermal & Information Entropy
這是普通熱力學最後的章節,我們來把前面Thermal和Information(Shannon) Entropy的概念連結在一起。
複習
Information Entropy (Shannon)
對於一個資訊量很大、自由度很高的系統,我們放棄去了解每一個粒子的運動,而是引進統計的概念,對想知道的系統變量定出 Random Variable,以及描述其的機率分布,接著便可進一步界定量化此系統不確定的方式(以銅版為例,正反面就是Random Variable,機率分布是Bernouli Distribution,不確定性在於你每擲一次,不知道會出現正面還是反面的結果),這個不確定性指標就是Shannon Entropy
\[\sigma \equiv \langle -\ln P \rangle = - \Sigma_s - P_s \ln P_s\]其中s為所有可能的state。
這個數值越大,代表系統的不確定性越大,「亂度」也越大。
而從之前簡單的Dog-Flea Model知道,此亂度會隨著時間逐漸上升到最大值之後維持平衡。
Thermal Entropy
而在熱力學中,我們就是畫個P-V圖,定義出熵
\[S(B)-S(A) = \int_A^B \frac{dQ}{T}\]如果是可逆的,積一圈回來就是0
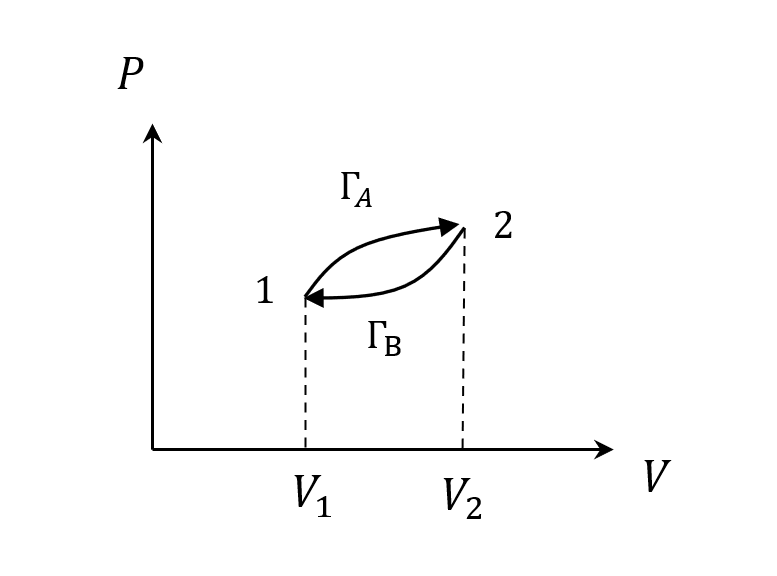
跟potential的概念很像,和路徑無關,只和端點狀態有關,所以Thermal Entropy是狀態函數。
微分形式
\[TdS=dQ\]Relation
有一個關係式可以連結這兩種Entropy
\[S=k\sigma\]其中k就是Boltzman constant。
接下來我們要從兩個角度證明這個公式
- 從熱平衡波茲曼分布出發
- 更General的從能量出發
證明一:波茲曼分布
假設現在有一個系統,和熱庫接觸並交換能量
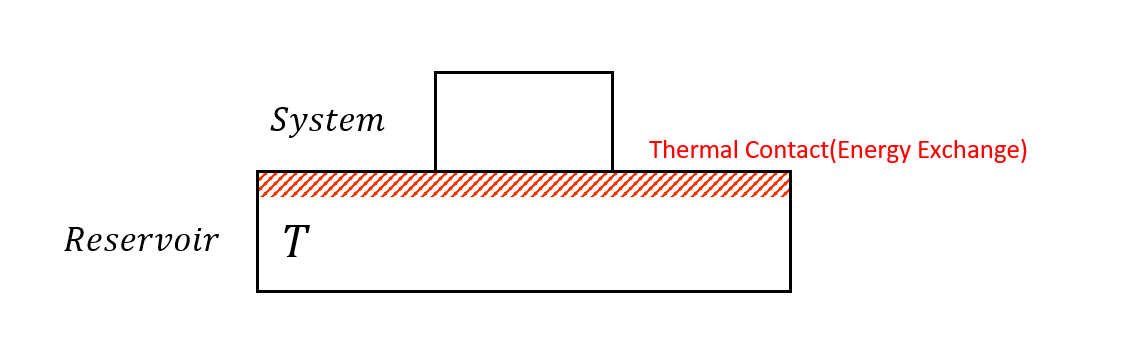
一旦在交換能量了,這個系統的能量就不再是定值,是Random Variable,必須用機率分布去描述。
假設達到熱平衡時狀態出現的機率分布滿足波茲曼分布
\[P_s\propto e^{\frac{-E_s}{kT}}\]波茲曼分布我們知道能量越低機率越高,所以可以想像就是這個系統一和熱庫接觸就會想偷懶XD
成正比我們用個正比常數
\[P_s=\frac{1}{Z}e^{\frac{-E_s}{kT}}\]已知所有狀態機率總和為1
\[\Sigma_s P_s = 1\]所以
\[\Sigma_s \frac{1}{Z}e^{\frac{-E_s}{kT}} = 1\\ \Rightarrow Z = \Sigma_s e^{\frac{-E_s}{kT}}\]這個$Z$稱為partition function分割函數。(其實就很像我們切個大餅,切1塊、2塊、4塊,那就是總共分成7塊。)
套用理想氣體
接著把這個套用到理想氣體上,但首先我們要先定義什麼是「狀態」?
狀態就是所有可能的狀態,想知道一個粒子在幹嘛,就要知道他在哪,會有多快。
因此在三維的世界裡,在哪$\vec{r}$,就要用$(x,y,z)$描述,多快$\vec{p}$也是用動量$(p_x,p_y,p_z)$,所以機率分布的變數有兩個,各自有三個分量
\[P(\vec{r},\vec{p})=P(x,y,z,p_x,p_y,p_z)\]所以我們得到每個狀態的能量
\[E_s=\frac{p_x^2+p_y^2+p_z^2}{2m}=\frac{p^2}{2m}\]所有的狀態積分會是
\[\Sigma_s=\Sigma_{\vec{r}}\Sigma_{\vec{p}}=\int dx \int dy \int dz \int dp_x \int dp_y \int dp_z\]這樣就能回來算分割函數
\[\begin{align} Z &= \Sigma_s e^{\frac{-E_s}{kT}}\\ &= \Sigma_{\vec{r}}\Sigma_{\vec{p}} e^{-\frac{1}{2mkT}(p_x^2+p_y^2+p_z^2)}\\ &= (\int dx dy dz)(\int_{-\infty}^{\infty} dp_x e^{-\frac{p_x^2}{2mkT}})(\int_{-\infty}^{\infty} dp_y e^{-\frac{p_y^2}{2mkT}})(\int_{-\infty}^{\infty} dp_z e^{-\frac{p_z^2}{2mkT}})\\ &=V(2\pi mkT)^{\frac{1}{2}}(2\pi mkT)^{\frac{1}{2}}(2\pi mkT)^{\frac{1}{2}}\\ &(\because \int_{-\infty}^{\infty}dz e^{-z^2}=\sqrt{\pi})\\ &=V(2\pi mkT)^{\frac{3}{2}}\propto VT^{\frac{3}{2}} \end{align}\]套用回Information Entropy
接著把這個理想氣體的波茲曼分布套回到Shannon Entropy
\[\begin{align} \sigma&=\langle - \ln P \rangle = \langle -\ln \left( \frac{1}{Z}e^{\frac{-p^2}{2mkT}} \right)\rangle\\ &=\ln Z + \frac{1}{kT}\langle \frac{p^2}{2m}\rangle \end{align}\]從之前溫度指標的定義
\[\bigg\langle \frac{1}{2}m(v_x^2+v_y^2+v_z^2)\bigg\rangle=\frac{3}{2}kT\]得到
\[\begin{align} \sigma &= \ln Z + \frac{3}{2}\\ &=\ln V + \frac{3}{2} \ln T +\sigma_0 \end{align}\]這就是對單一粒子的Shannon Entropy,後面常數項其實有普朗克常數,詳情可看Sockur-Terode Equation。
因為是理想氣體,所以整個系統假設有N個粒子,彼此互相獨立
\[\sigma_N=N\cdot \sigma = N \ln V + \frac{3}{2} N \ln T + const\]我們用之前簡單的cycle來看
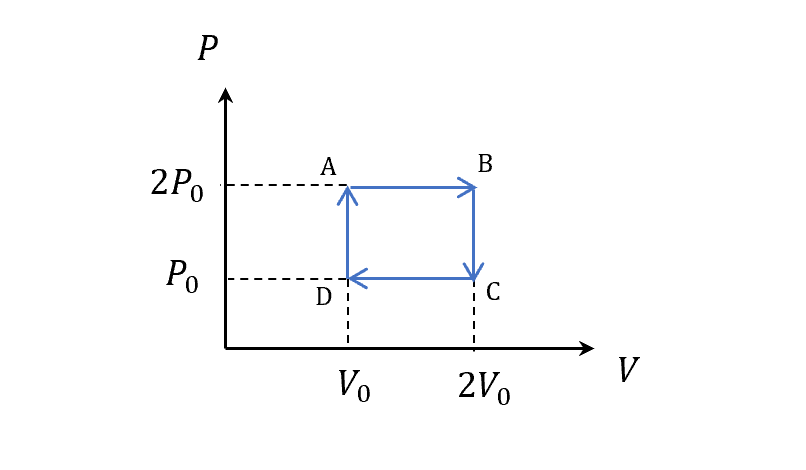
一樣取這段算Thermal Entropy
\[S(B)-S(A)\\ =nC_p \ln 2\\ =\frac{5}{2}nR\ln 2\\ =\frac{5}{2}Nk\ln 2\]兩者比較就得證至少對理想氣體來說
\[S=k\sigma\]小結思路
之前我們用一個簡單的square cycle,知道理想氣體積一圈,Thermal Entropy沒變,然後也可以取各自一段來算Entropy的差。
現在直接單純看粒子本身,我們不知道粒子在哪裡,所以用機率分布去描述他,看他在哪裡$\vec{r}$、並用多快$\vec{p}$的方式出現,且這個機率分布滿足波茲曼分布,算出來之後,就可以把這個機率分布帶進Information Entropy,算出來之後就可以針對每一點Entropy算差。
結果發現,這樣的方式去算每一點的Shannon Entropy的差,和之前用吸熱放熱的Thermal Entropy的差,居然是一樣的,只是中間差了一個波茲曼常數$k$。
不同角度出發得到一樣的結果,代表我們用熱去理解Entropy本身有更深刻的意義,等下會看到熱這件事情和機率分布有什麼關聯!
Maxwell distribution
那先岔開話題一下,我們順便來推導Maxwell的”速率”機率分布。
前面提到的Boltzman distribution是所有熱平衡都會滿足的,要知道粒子在哪裡以及多快,當經過適當的變形之後,若只需要知道多快,就可以變成Maxwell distribution for molecular speed。
首先我們定義一個Quantity和速率有關,去算期望值
\[\langle Q(v) \rangle=\Sigma_{\vec{r}}\Sigma_{\vec{p}}\frac{1}{Z}e^{-\frac{p^2}{2mkT}}Q(v)\\ =V\frac{1}{Z}\int dp_x \int dp_y \int dp_z e^{-\frac{mv^2}{2kT}}Q(v)\]因為 v 和 r 無關,積r可以單獨先積起來是體積V。
\[=V\frac{1}{Z} \int dv_x \int dv_y \int dv_z m^3 e^{-\frac{mv^2}{2kT}} Q(v)\\ (\because \int dp_x = m \int dv_x )\\ =\left(\frac{m}{2\pi kT}\right)^{\frac{3}{2}} \int dv_x \int dv_y \int dv_z e^{-\frac{mv^2}{2kT}} Q(v)\\ (\because \frac{1}{Z}=\frac{1}{V}\left(\frac{1}{2\pi mkT}\right)^{\frac{3}{2}})\\ =\int_0^\infty dv \left(\frac{m}{2\pi kT}\right)^{\frac{3}{2}} 4\pi v^2 e^{-\frac{mv^2}{2kT}} Q(v)\]最後這個轉換是我們可以把xyz的小方塊積分,畫成球殼積分如下圖
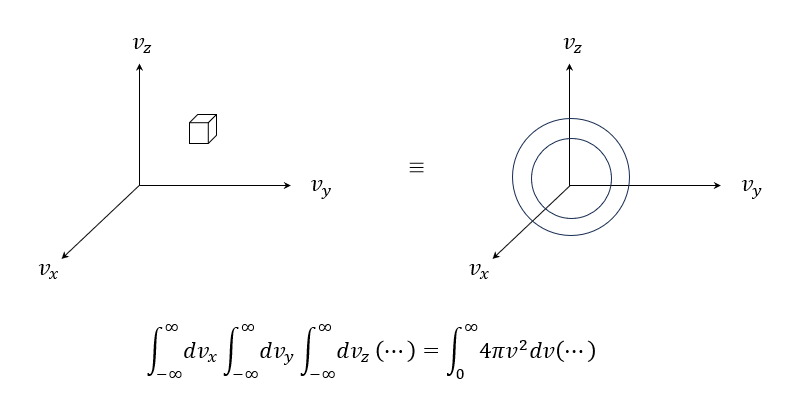
比對一下原本期望值的定義
\[\langle Q(v) \rangle = \int_0^\infty dv p(v) Q(v)\]則
\[p(v)=\left(\frac{m}{2\pi kT}\right)^{\frac{3}{2}} 4\pi v^2 e^{-\frac{mv^2}{2kT}}\]就是速率的機率分布!從波茲曼分布的六重積分,化成Maxwell只有速率的一重積分。
畫個圖看一下,可以看到之所以會先上來再下去是兩個原因
- 氣體仍然越懶越好,最好不要跑不要動,沒有什麼所謂的中庸之道
- 現在這條線畫的不是粒子某個狀態出現的可能性,而是一種速率的可能性有多少。一個速率可以有很多種方向的可能(degeneracy),所以速率越大,各種方向(幾何$4\pi v^2$影響)形成的可能性越大,。
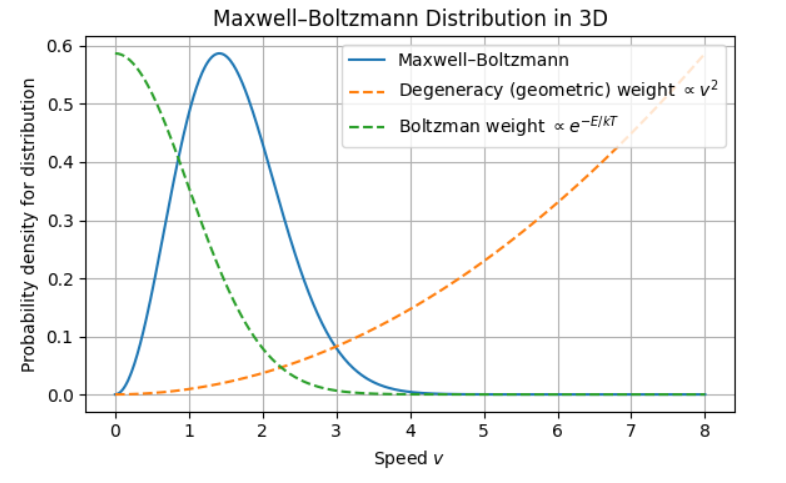
這裡也附上1D和3D的比較圖,可以看到1D的就是Boltzman Distribution了,沒有degeneracy的問題!

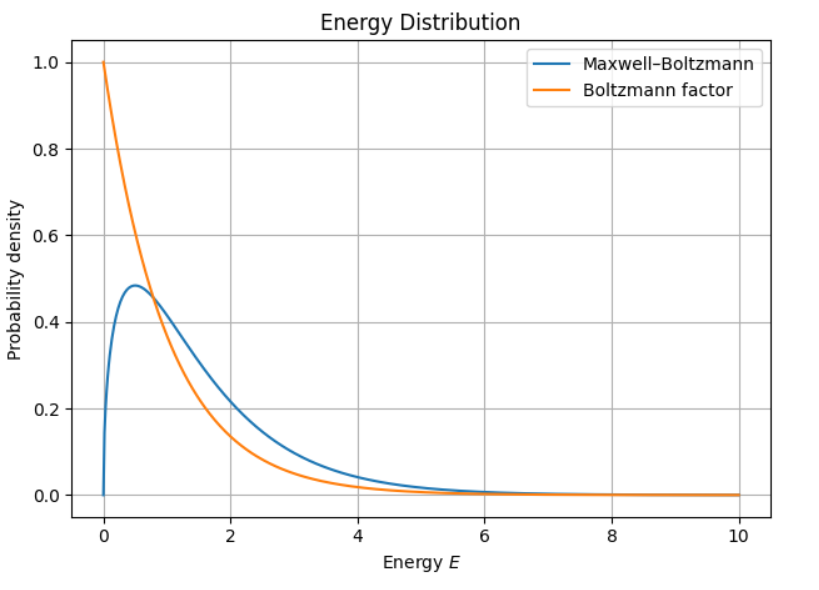
最後如果把兩個Distribution放在一起,因為Boltzman算的是速度+空間,所以我們換算到能量來看
證明二:General 能量出發
先講結論,Information Entropy可以推導Thermal Entropy,但是反過來不行!
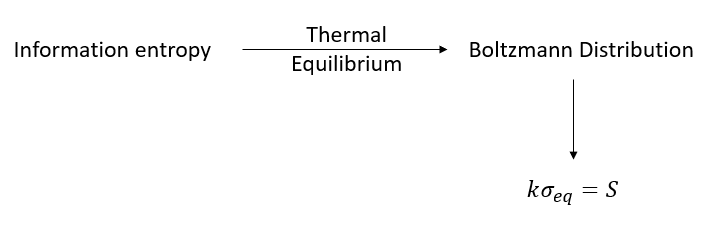
從genral 的 Information entropy出發,在熱平衡的情況下,可以得到波茲曼分布,並算出Information entropy在熱平衡的情況下,乘上$k$就是Thermal entropy。
\[k\sigma_{eq}=S\]所以Information entropy比Thermal entropy更廣泛的。
我們在複習一下亂度的概念,就是在描述系統的時候,發現DOF太大,或是不再只是DOF,反正就是outcome(random variable)不是確定的時候,就必須使用機率分布,然後就能定義Information entropy。
所以只要你對某件事情不確定,就都可以定義出Information Entropy。
但是有一種一定程度的不確定很特別,就是只要某個東西和另一個東西達成熱平衡,就會有一個特別的分布,就是波茲曼分布。而這個情況下對應到的Information entropy,剛好和吸熱放熱這種概念出來的Thermal entropy是等價的!
所以真正把Information entropy和Thermal entropy拉在一起的人,就是波茲曼分布(Boltzmann Distribution),若你的分布不是波茲曼,這兩種entropy就沒有關聯。
計算平均能量的改變
一個系統的平均能量定某一個state的能量乘上該機率
\[U\equiv \Sigma_s P_s E_s\]取小變化,可以看到平均能量變化改變有兩種可能,一種是機率分布改變,另外一個是能量改變。
\[dU=\Sigma_s E_s dP_s + \Sigma_s P_s dE_s\]我們可以簡單圖示化一下,假設有一個能量樓
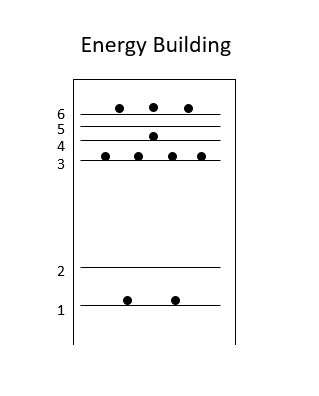
假設你現在要提升能量,那就有兩種辦法
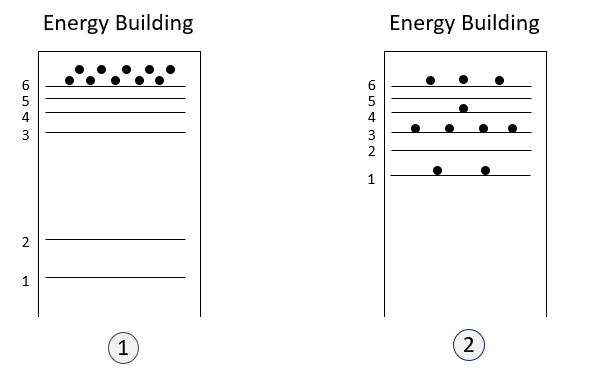
- 所有人都搬到6樓:結構沒有改變,只是分布改變 $\Sigma_s E_s dP_s$,而這個辦法就是吸熱$dQ$。(慫恿群眾熱情XD)
- 大家都住在原本的樓層,但是改變樓層的高度:代表的是能階改變 $\Sigma_s P_s dE_s$,這個辦法就是系統對外(或是外面對系統)做功 $-dW$。(拆樓改變結構作功) (這邊附註說明一下,在量子力學的世界裡,體積改變會改變能階,可以簡單看位能井的公式)
所以套回理想氣體,改變能量就是加熱,沒有改變裡面能階結構,但氣體分布改變。另外一種方式就是作功(壓他),但沒有改變分布,只是改變能階高度。
能階改變
現在來推導
\[\Sigma_s P_s dE_s = -dW\]來改寫
\[\Sigma_s P_s dE_s\\ =\Sigma_s P_s \vec{\nabla}E_s \cdot d \vec{r}\\ =-[\Sigma_s P_s (-\vec{\nabla}E_s)]d \vec{r}\\ =-\langle \vec{F} \rangle \cdot d\vec{r}\\ =-dW\]- 第一個等於用微積分換算一下
- 第二個等於因為Summation和r無關,所以提出來
- 第三個等於能量做gradient就是力,力乘上各自機率取平均就是期望值
藉由改變能量會牽扯到力,力會牽扯到功。
you need to do some work to reconstruct the energy structure.
分布改變
現在來推導
\[\Sigma_s E_s dP_s = dQ\]已知
\[\sigma\equiv \Sigma_s -P_s \ln P_s\] \[d\sigma=-\Sigma_s (\ln P_s dP_s + P_s \frac{1}{P_s} dP_s)\\ =-\Sigma(\ln P_s + 1) dP_s\]然後放進波茲曼分布
\[\ln P_s = -\ln Z - E_s / kT\]代進去
\[d\sigma = (\ln Z - 1) \Sigma_s dP_s + \frac{1}{kT} \Sigma_s E_s dP_s\] \[\because \Sigma_s P_s = 1 \rightarrow \Sigma_s dP_s = 0\] \[\Rightarrow d\sigma = 0+\frac{1}{kT} \Sigma_s E_s dP_s\\ \Rightarrow \Sigma_s E_s dP_s = kT d\sigma\]結合
所以回到原本平均能量的改變
\[dU=\Sigma_s E_s dP_s + \Sigma_s P_s dE_s = kT d\sigma - dW\]dQ的定義
跟熱力學第一運動定律做比較,就可以得到
\[kT d\sigma = dQ\]只要相信能量守恆,以前定義$dQ$的方式就是$dU$和$dW$算出來,不見的就算$dQ$。
但這裡知道heat就是在不改變能階的結構下造成的能量變化,不改結構,改分布。而這個對應的就是微觀的,因為一棟樓裡面的人搬家,你外面也看不到。
而作功就是在維持同樣的分布底下,把樓拆了重蓋,不改分布,改結構。樓都重蓋了,你經過就能宏觀地看到改變。
再強調一次,能量變化的兩個來源
- 熱:不改結構,改分布
- 功:不改分布,改結構
推導平衡態 Information Entropy
所以最後這個熱的公式
\[dQ = kT d\sigma\\ TdS = kT d\sigma\\ S = k\sigma\]這個跟證明一的方法不同,不是只有for理想氣體,而是更加general的形式!
小結
至今學到的過程思路是這樣的,我們要問的問題是如何去量化一個系統的不確定性?
從古典想法,會認為能量在交換的時候,有些能量看不太見,但在相信能量守恆的情況下,把這些不知道的叫做熱。 然後又知道另外一個指標叫做溫度,神奇的是把溫度除以熱積一整圈不會變,然後定這個是Entropy。
而從現代出發,我們知道達成熱平衡也可以交換能量,此時系統能量是不確定的,需要用機率去描述他,這個機率分布是波茲曼分布,然後Shannon告訴我們你只要知道機率分布長什麼樣子,就能定出Information Entropy,就能知道不確性是多少。
接著計算能量改變時,發現能量改變有兩種來源,一個是分布改變,一個是結構改變,其中分布改變就是熱。至此,我們釐清了在古典中有點虛幻的熱定義是什麼。
並且這個能量變化有一個溫度T,T是來自於波茲曼分布,所以可以進一步地說,如果這個系統的能量是完全已知的,那溫度這個概念就是沒有用的。溫度只有在能量會浮動的情況下加上是波茲曼分布的情況下有用。
舉個簡單的例子,如果我們現在隨便把一個東西往窗外丟下去,需不需要對這個越摔越快的情況下定義出溫度?不需要!因為在忽略空氣阻力的效應底下,我們可以直接算出速度和所有東西,所以能量已知,就不是random variable,就不會有機率分布。不會有波茲曼分布,就沒有溫度,就不需要溫度的概念了。
另外一個例子是若是現在隨便丟一個銅板,雖然outcome的確是未知的,有random variable,但他遵循的是Bernoulli分布,正面1/2,反面1/2,不是遵循波茲曼分布,就也不需要溫度。
所以至此,我們知道一個東西要有溫度,代表這個系統夠亂,還必須遵循波茲曼分布的亂才有溫度。
