(3) 熱力 ─ 熱力學第一定律
前言
現在有一盒氣體,開口處有活塞可以動,氣體可以對外面做功($W$),現在把這個系統放在火爐上加熱,會發生什麼事情呢?
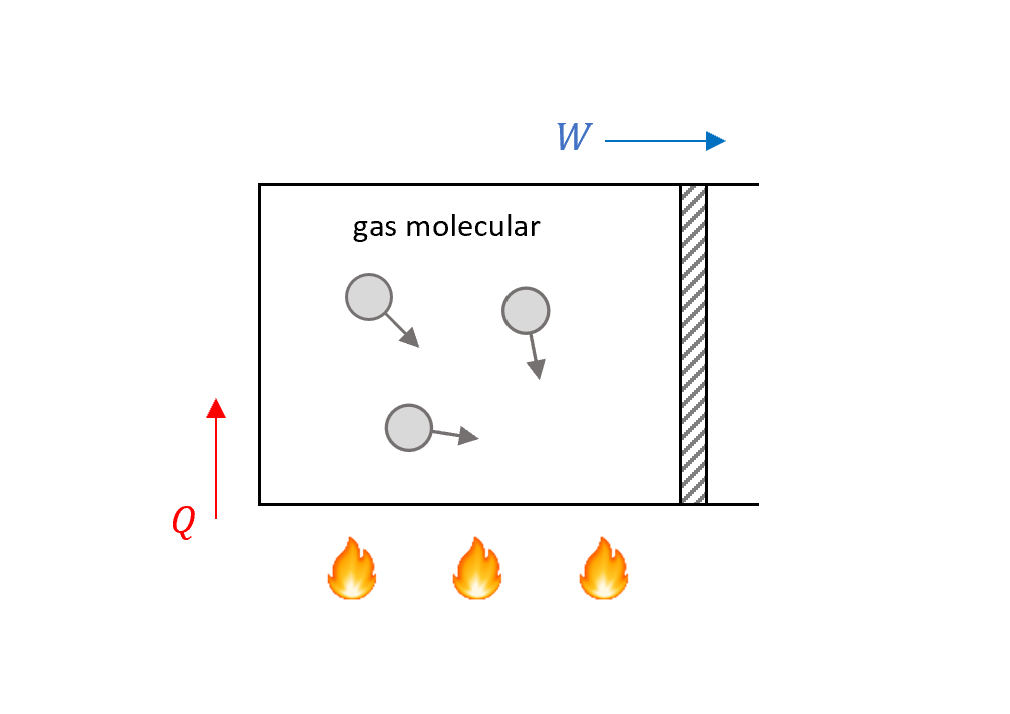
很直覺的我們知道會有熱量從火爐給氣體分子,在這裡我們定義$Q$正為吸熱,負會放熱,如圖所示:
\[Q:\text{heat absorbed by the gas}\]然後活塞也可以動:
\[W:\text{work done by the gas}\]其他的熱則可以改變氣體自己的能量,所以簡單得到這個式子
\[\underbrace{Q}_{\text{heat}}=\underbrace{\Delta U}_{\text{change of internal energy}} + \underbrace{W}_{\text{work}}\]這就是熱力學第一定律的公式啦!把熱當作能量的轉換。
白話就很像$Q$是我們的薪資收入(吸收的熱),$W$是花費(對外做功),$\Delta U$是帳戶的錢(改變自己的內部能量)。
但是,雖然感覺是常識,其實還有很多模糊的地方,譬如說什麼叫做對外做功?做了什麼功?還有改變內部能量是什麼能量?為什麼加熱的物理量稱作Heat?這個Heat具體要怎麼算?
往後我們會越來越明白的。
能量守恆看熱力學第一定律
首先我們列出能量守恆的公式
\[\Delta\left(\frac{1}{2}Mv^2_{cm}+U_{ex}+E_{in}\right)=W_{nc}\]稍微說一下每一項:
- 第一項是質心運動。
- 第二項$U_{ex}$是守恆的外力造成的potential engery。
- 第三項$E_{in}$是內能,這裡的內力在理想氣體的系統中我們設是保守的(conservative),畢竟你沒有碰過拿一個裝著氦氣的氣球,走一走這些氣體就黏在一起,氣球就縮小。所以這裡的內力都屬於彈性碰撞。
- 第四項$W_{nc}$是非守恆的外力作功。
移項一下
\[\Delta\left(\frac{1}{2}Mv^2_{cm}+E_{in}\right)=W_{nc,ex}-\Delta U_{ex}=W_{ex}\]通稱是$W_{ex}$外力作功。
接著我們假設這個理想氣體的系統沒有質心的加速運動(譬如說沒有要去算整盒氣體往下丟的情況),所以簡化為內能的變化等於外力作功。
\[\Delta E_{in}=W_{ex}\]再來回顧一下我們的系統,是在某個平衡態,所以外界對系統作功,就是負的系統對外界作功(作用力與反作用力),如下圖
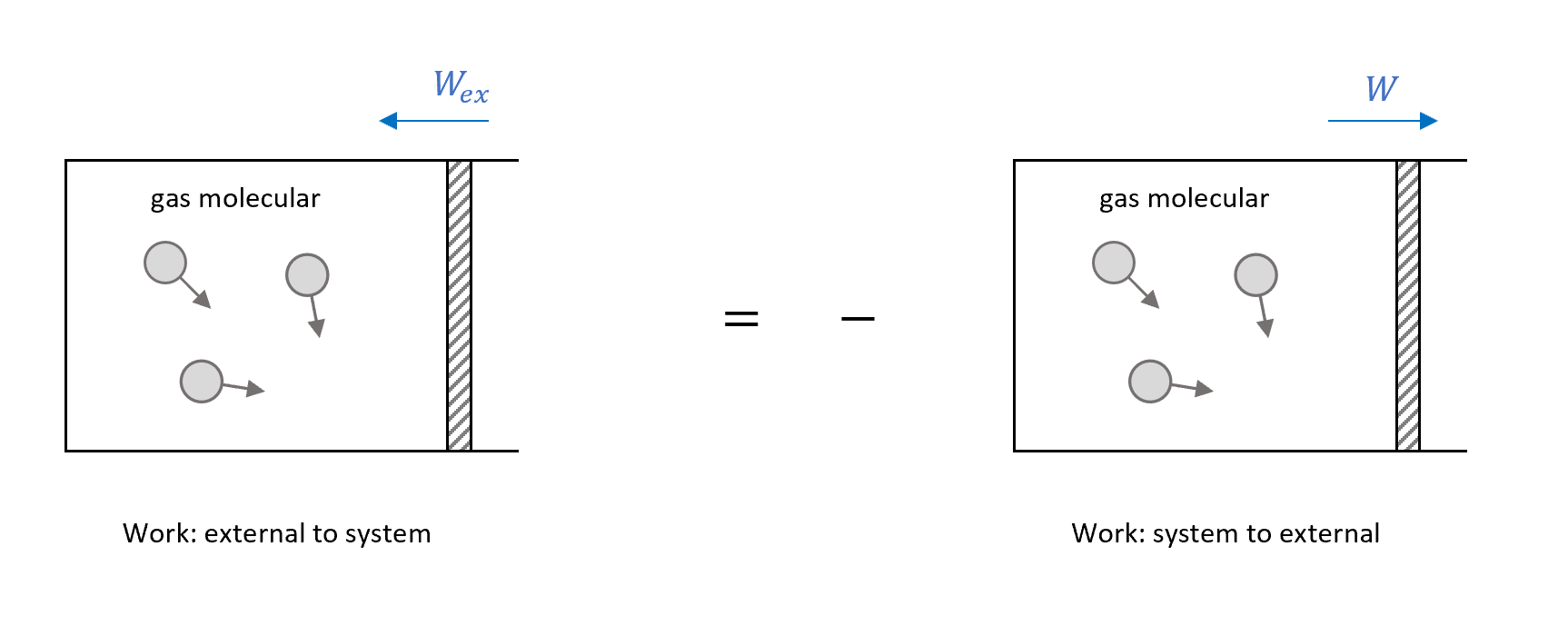
再來是這裡的$\Delta E_{in}$是對系統在某個瞬間測量到的,不會是定值,所以我們取ensemble average作統計平均。
因此整理簡化得
\[\Delta U = - W\Rightarrow \Delta U + W = 0\]但這樣很奇怪,按照前言的例子,帳戶的少的錢直接是花費的錢,那麼熱呢?熱去哪裡了?
外力分為微觀和宏觀
實際上,外力要分成微觀和宏觀:
\[W_{ex}=W_{micro}+W_{macro}\]其中微觀的外力(碰撞)我們稱為熱。
\[W_{micro} = Q\]宏觀的外力是我們人眼可看見的變化(e.g., 體積形狀)
\[W_{macro} = -W\]因此回來公式,內能的變化等於熱減掉宏觀的作功
\[\Delta U = W_{ex} = Q-W \Rightarrow Q=\Delta U+W\]這就是我們前言一開始的熱力學第一定律公式。
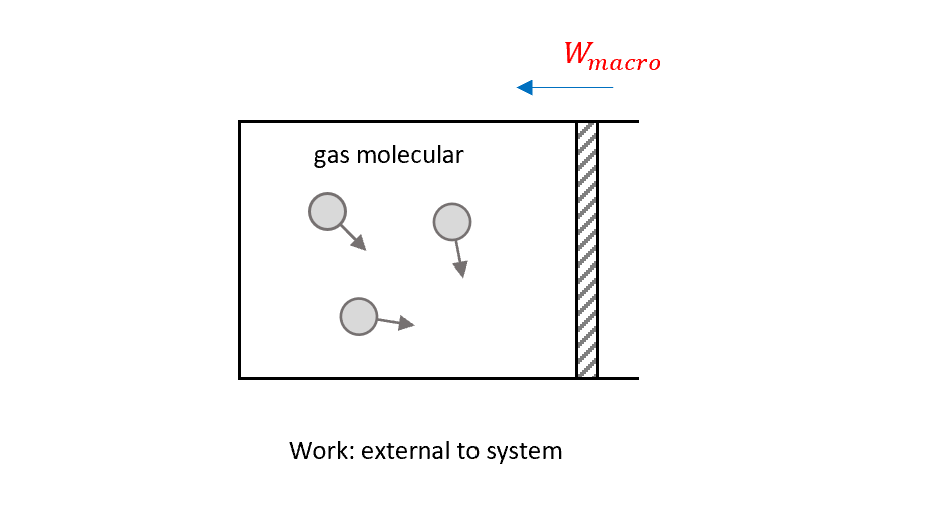
是到後來統計力學出來之後,可以去看微觀的碰撞和交換能量等機制,更確定了熱力學第一定律。
計算作功$W$、內能$\Delta U$、熱量$Q$
那一樣繼續這個系統,我們來算這三個物理量吧!
首先假設板子移動$\Delta x$
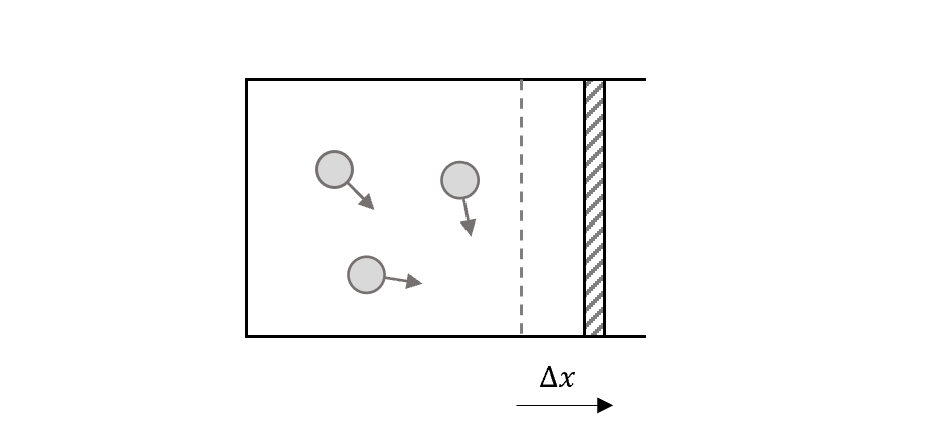
如果壓力不是定值,就切小塊來積分
\[W=\Sigma_{i}P_i\Delta V_i\\ W=\int PdV\]假設現在是等溫過程的膨脹(isothermal expansion),溫度是常數,我們可以畫出這個圖
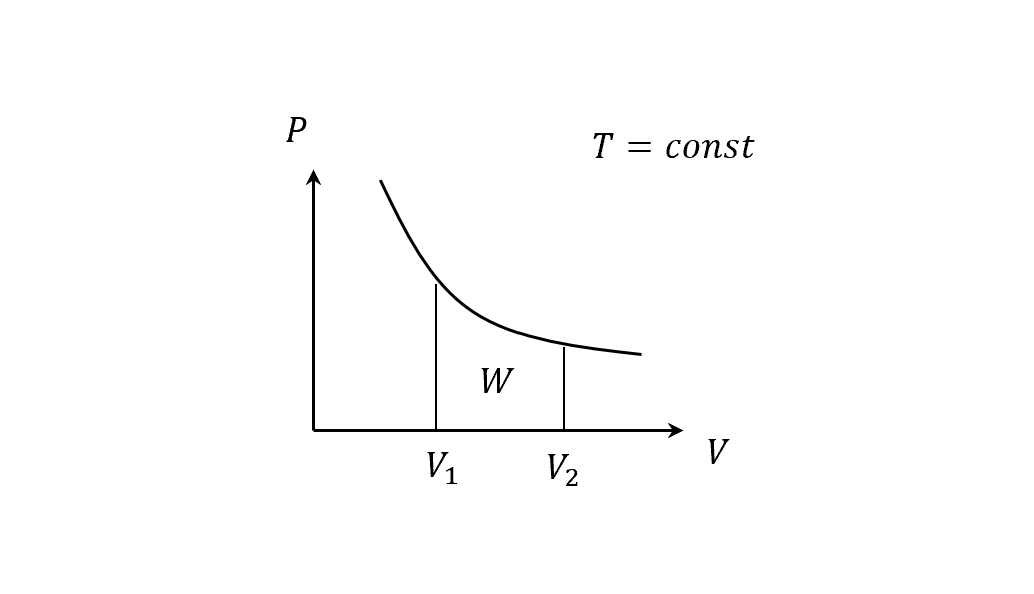
所以
\[\begin{align} PV&= NkT = const\\ P&=\frac{NkT}{V}\\ W&=\int PdV = NkT\int_{V_1}^{V_2}\frac{1}{V}dV\\ &=NkT \ln V \bigg|_{V_1}^{V_2}\\ &=NkT (\ln{V_2}-\ln{V_1})\\ &=NkT \ln\left(\frac{V_2}{V_1}\right) > 0 (\because V_2 > V_1) \end{align}\]再來算內能,從上一章節的熱平衡我們知道
\[\langle u \rangle = \bigg\langle \frac{1}{2}mv^2\bigg\rangle=\frac{1}{2}kT\]三維的話就同理
\[\langle u \rangle = \bigg\langle \frac{1}{2}m(v_x^2+v_y^2+v_z^2)\bigg\rangle=\frac{3}{2}kT\]這是只有一個分子的情況,若是全部有N個
\[U=N\cdot\langle u \rangle = \frac{3}{2}NkT\]變化
\[\Delta U = \frac{3}{2}Nk\Delta T = 0 (\because\text{ isothermal})\]注意這只是理想氣體的近似。
這樣有了$\Delta U$有了$W$,我們可以算熱量
\[Q=\Delta U + W = NkT \ln\left(\frac{V_2}{V_1}\right)\](這裡附註一下,那這樣上一章節在算的熱平衡,其實就是假設體積都沒變沒有宏觀做功,只看內能和熱量的關係。)
