(6) 熱力 ─ Entropy 熵簡介
這節開始來講熵,口說同音稱商,火字旁為取自熱力學(thermaldynamic variables),商則因為其公式為 $\frac{\text{熱}}{\text{溫度}}$。
到現在熱和溫度其實都還是有點小抽象,所以Entropy (S) 在學習的時候也常常會有點困惑,但反正我們現在繼續來看吧~
現在來看個系統,有兩種狀態,從狀態一到狀態二有很多路徑可以到,我們定兩條
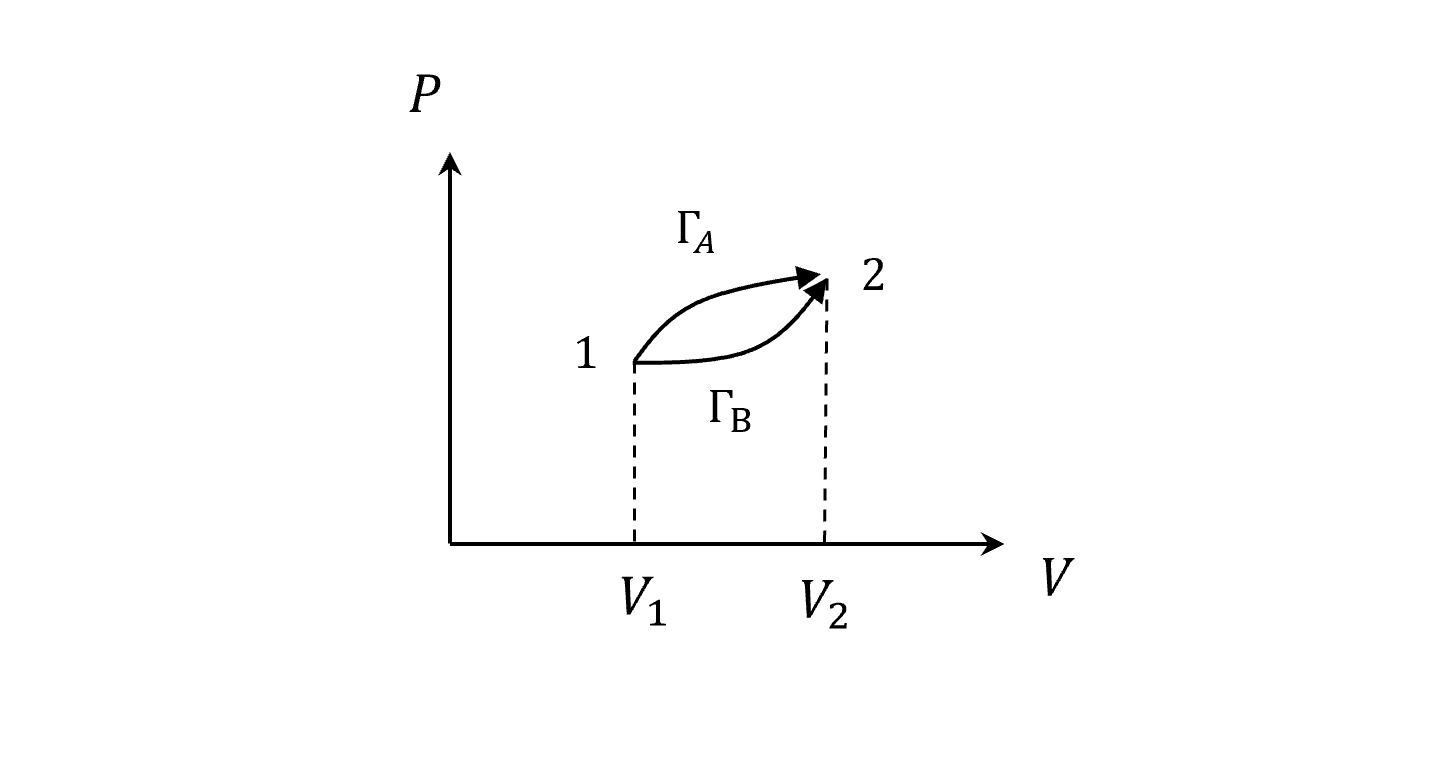
算做功
\[W_A=\int_1^2PdV\\ W_B=\int_1^2PdV\]因為面積就是做功,很明顯的看出來
\[W_A\neq W_B\]所以我們來換一下,不看端點,用路徑分
\[W_A=\int_{\Gamma_A} PdV\\ W_B=\int_{\Gamma_B} PdV\]上一節講等溫和絕熱不用管路徑的原因,因為當我們說「等溫」和「絕熱」的時候,路徑已經決定好了,只有唯一路徑,所以直接用端點看狀態來求做功。
Thermal Cycle
現在我們積一圈回來
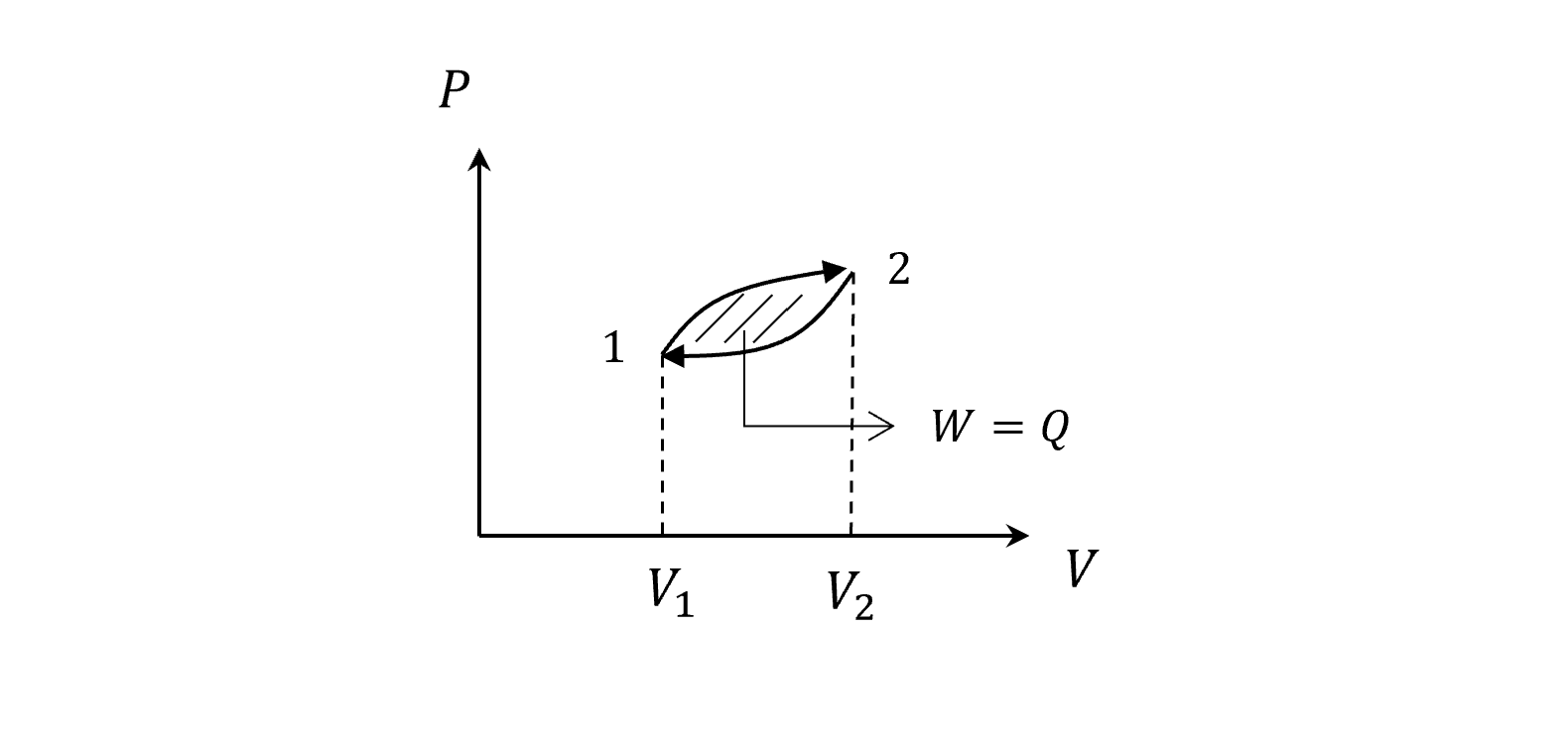
因為內能只和溫度有關,積一圈回來,同樣的PV,T也一樣,那麼圈內面積就是這個cycle的功和吸的熱
\[\Delta U = 0\\ W=Q=\text{Enclosed area}\]微分式
\[W=\oint dW \neq 0\\ Q=\oint dQ \neq 0\\ \Delta U = \oint dU = 0\rightarrow U\text{ is a state function}\]所以看cycle(引擎)的時候不是只看狀態的結果,不同的過程會不同,不同的過程才決定了引擎的好壞。
竟然熱量和功積一圈不會等於0,我們回頭來看另外一個積一圈會等於0的公式(注意這裡只有可逆時才成立,代表積一圈時,沒有能量號散,像是不可回復的摩擦力作用在裡面。假若真的不可逆的話,那此公式就會>0):
\[\oint \frac{dQ}{T}=0\]證明比較複雜,我們直接舉個例子。
舉例:可逆 Thermal Cycle
複習一下熱力學第一定律微分形式
\[dU = dQ-PdV\\ \Rightarrow \frac{dQ}{T}=\frac{dU}{T}+\frac{P}{T}dV\]然後舉個簡單例子,分成四個變化路徑如圖
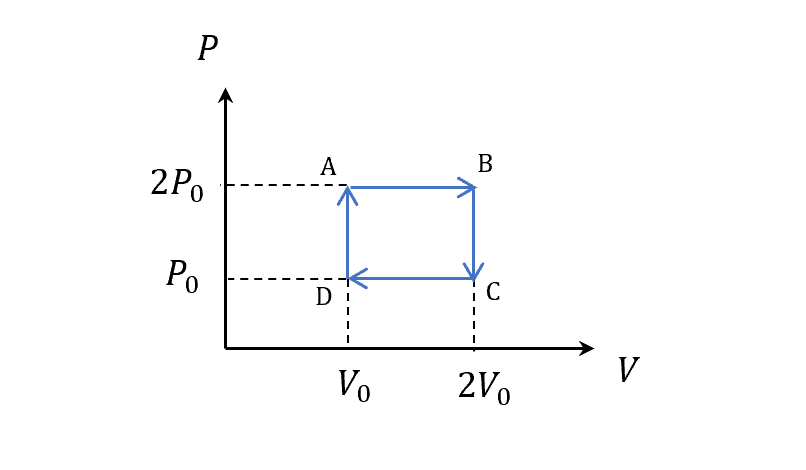
分段路徑積分
等壓膨脹 $A\to B$
定個符號$S$
\[\begin{align} S_{A\to B} &\equiv \int_A^B \frac{dQ}{T}=\int_A^B \frac{dU}{T}+\frac{P}{T}dV\\ &=nC_v\int_A^B \frac{dT}{T}+nR\int_A^B \frac{dV}{V}\\ &(\because dU=nC_v dT,\quad T=\frac{PV}{nR})\\ &=nC_v\ln \left(\frac{T_B}{T_A}\right)+nR\ln\left(\frac{V_B}{V_A}\right)\\ &=n(C_v+R)\ln 2\\ &=nC_p \ln 2\\ &(\because \frac{T_B}{T_A}=\frac{4P_0 V_0}{2P_0 V_0}) \end{align}\]定容壓縮 $B\to C$
\[\begin{align} S_{B\to C} &\equiv \int_B^C \frac{dQ}{T}\\ &=nC_v\int_B^C \frac{dT}{T}\\ &=nC_v\ln \left(\frac{T_C}{T_B}\right)\\ &=nC_v\ln \frac{1}{2}\\ &=-nC_v \ln 2 \end{align}\]等壓壓縮 $C\to D$
\[\begin{align} S_{C\to D} &\equiv \int_C^D \frac{dQ}{T}\\ &=nC_v\ln \left(\frac{T_D}{T_C}\right)+nR\ln\left(\frac{V_D}{V_C}\right)\\ &=-nC_p\ln 2 \end{align}\]定容加壓 $D\to A$
\[\begin{align} S_{D\to A} &\equiv \int_D^A \frac{dQ}{T}\\ &=nC_v\int_D^A \frac{dT}{T}\\ &=nC_v\ln \left(\frac{T_A}{T_D}\right)\\ &=nC_v\ln 2 \end{align}\]總和
全部拼起來
\[\begin{align} \oint\frac{dQ}{T}&=S_{A\to B}+S_{B\to C}+S_{C\to D}+S_{D\to A}\\ &=nC_p \ln 2+(-nC_v \ln 2)+(-nC_p\ln 2)+nC_v\ln 2\\ &=0 \end{align}\]狀態函數 熵 Entropy
這樣積一圈回來等於0,其實就很像是某種potential(像是以前學的保守力),這樣的狀態函數我們定為 Entropy,僅和狀態有關,和路徑無關。
\[\frac{dQ}{T} = dS\\ dQ=TdS\]Entropy is a state function.
所以任意PV圖的兩個點,我們可以計算差值,並只看端點狀態
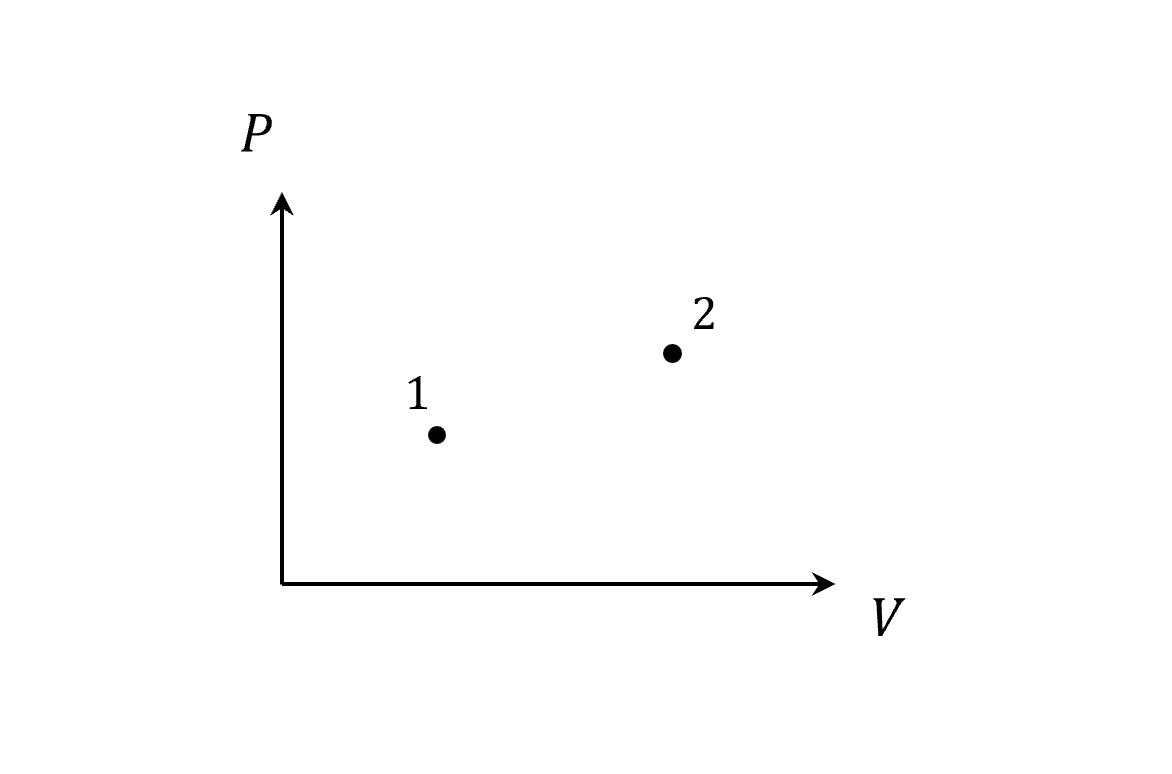
從 $dS$ 看凌亂程度
現在我們進一步來看$dS$的特性,先分別畫出各個狀態下的氣體狀況
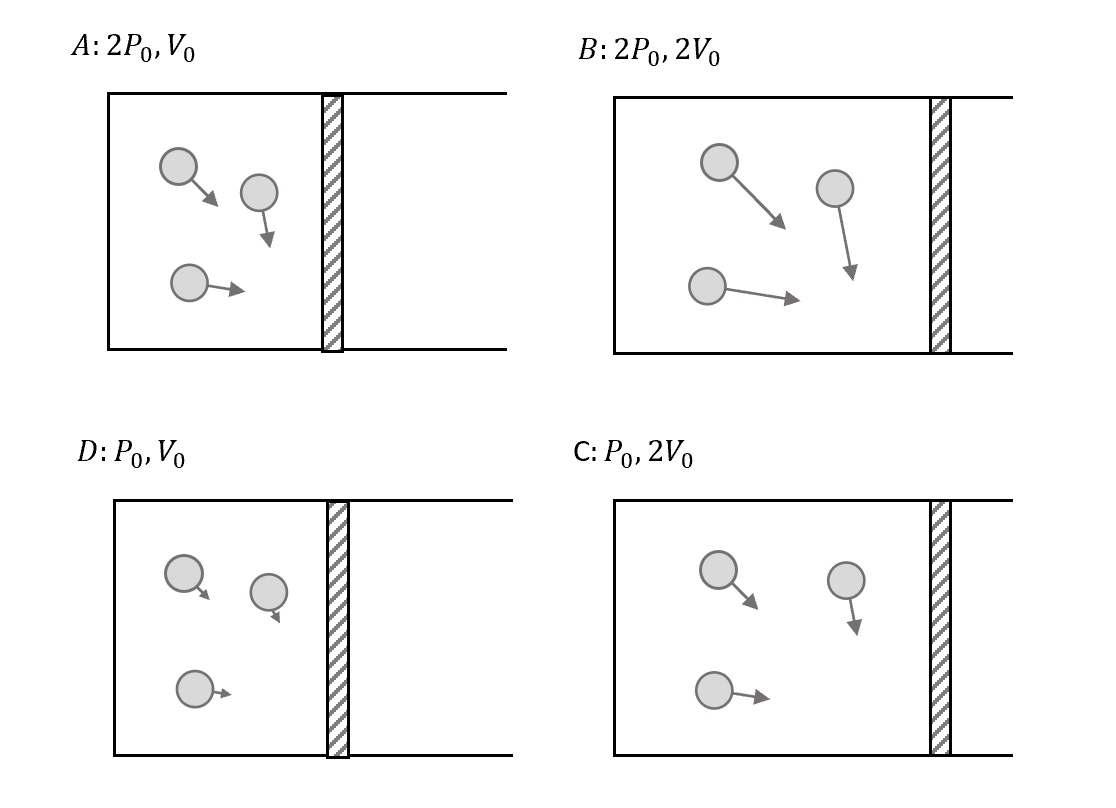
這樣就可以來對每個狀態的Entropy進行排序的關係式了!
\[S(B) > S(C) > S(A) > S(D)\]溫度的話就是PV相乘,所以
\[T(B) > T(C) = T(A) > T(D)\]那這個大小有什麼意義呢?我們可以用來判斷該系統的凌亂程度。
首先我們來看為什麼 $S(B) > S(C)$。
先看兩者的空間,都是$2V_0$,空間一樣亂,但是溫度因為B比較大,速度上B較亂,所以整體的$S(B)$就會比較亂。
同理來看 $S(C) > S(A)$,雖然溫度一樣,所以速度一樣亂,可是C可以亂的空間比較大,所以整體的$S(C)$就更亂。
其他$A,D$和$B,C$也同理。
所以在統計力學上面,可以把Entropy S 和 “the degrees of disorder” 的概念連結在一起,去定量的描述這個系統的亂的程度。
古典小結邏輯:畫PV圖,發現大部分物理量積一圈幾乎都不是零,但是把$dQ/T$去積一圈卻是零,告訴我們可以定義像位能一樣的東西,就是Entropy,定義出來之後,我們用常識把Entropy把不同狀態做比較,產生了概念,定義出來的Entropy似乎跟系統的凌亂程度有關係。
