(5) 熱力 ─ 等溫膨脹及絕熱膨脹

複習一下，第三節我們從能量守恆出發，得出了熱力學第一定律

\[\Delta U = Q-W\]

系統(理想氣體)的內能改變，等於微觀做功(熱)減掉宏觀做功，這個我們通常意象的加熱微觀膨脹給的能量就是熱(Heat)。

所謂的宏觀和微觀差別就在於熱力變數(Thermodynamics variable)，溫度和體積是否有可見的變化。

接下來我們要繼續討論兩個系統，等溫膨脹及絕熱膨脹。

等溫膨脹

這個其實一樣在第三節討論過了，因為系統溫度一樣沒有變化，所以

\[\Delta U = 0\\ W=Q=NkT\ln\left(\frac{V_2}{V_1}\right)\]

所以吸熱的時候就會拿來做功做等溫膨脹($V_2>V_1$)。

理想氣體方程式

那麼理想氣體方程式

\[PV=NkT\]

因為等溫，所以就會是常數

\[PV=\text{const}\]

就是波以爾定律。

絕熱膨脹

現在系統處在絕熱環境下，代表沒有其他的熱會進來，系統中的熱也不會出去，簡單就是說

\[Q=0\]

所以熱力學第一定律得

\[\Delta U = -W\]

若是膨脹，做正功，則

\[\Delta U = -W < 0\]

溫度就會下降($T$↓)。

故而絕熱膨脹對外做功後系統溫度會下降。

理想氣體方程式

因為現在多了溫度的變數，就不再是直接的波以爾定律，需要重新整理。

我們現在有的公式

\[\begin{cases} \Delta U = -W < 0\\ PV = NkT\\ nC_v\Delta T = \Delta U = -\int P dV\\ \gamma = \frac{C_p}{C_v}=\frac{5}{3} \end{cases}\]

第三項是用我們第四節的推導，用定容來表示內能。

可是其實滿難解的，因為我們只有兩條公式，理想氣體是代數方程，定容是積分式，然後有三個變數$P,V,T$未定，所以我們換個想法，改求微分式$dP,dV,dT$。

(這裡有個概念，通常取微分之後，因為微分和微分相乘都會是很小的數字通常可先忽略，這時很容易就可以有一些線性關係出來，然後求微分方程就好了。)

所以理想氣體方程

\[d(PV)=d(NkT)\\ VdP+PdV=NkdT=nRdT\]

定容積分式

\[nC_v dT = -PdV\]

(兩邊同取積分其實就回到原本的($\because \int nC_vdT=nC_v\Delta T$)。

接著前者乘上$C_v$，後者乘上$R$，得到

\[\begin{align} C_v VdP &+ C_v P dV - nC_v R dT = 0\\ &+RPdV+nC_vRdT = 0 \end{align}\]

兩者相加得

\[C_vVdP+(C_v+R)PdV = 0\\ C_vVdP+(C_p)PdV = 0\\ VdP+\frac{C_p}{C_v}PdV = 0\\ \frac{dP}{P}+\gamma \frac{dV}{V}=0\]

就是微分方程式了，接下來來解。

先統一積分，從原先狀態到後面狀態

\[\int_1^2 \frac{dP}{P}+\gamma \frac{dV}{V}=0\\ \ln P \bigg|_1^2+\gamma \ln V\bigg|_1^2=0\\ \ln \frac{P_2}{P_1}+\gamma \ln \frac{V_2}{V_1}=0\\ \ln \frac{P_2}{P_1}+\ln \left(\frac{V_2}{V_1}\right)^\gamma=0\\ \ln \left(\frac{P_2}{P_1}\left(\frac{V_2}{V_1}\right)^\gamma\right)=0\\ \left(\frac{P_2}{P_1}\left(\frac{V_2}{V_1}\right)^\gamma\right) = 1\\ P_2 V_2^\gamma = P_1 V_1^\gamma = \text{const}\]

至此我們得到結果

\[PV^{\frac{5}{3}}=\text{const}\]

驗證

這裡稍微驗證一下，我們代入做功

\[W=\int_{V_1}^{V_2}PdV=\text{const}\int_1^2\frac{dV}{V^{\gamma}}=\text{const}\frac{V_2^{(1-\gamma)}-V_1^{(1-\gamma)}}{(1-\gamma)}\]

又

\[P_2 V_2^\gamma = P_1 V_1^\gamma = \text{const}\]

反正都是一樣的常數，所以再代回去得到

\[\text{const}\frac{V_2^{(1-\gamma)}-V_1^{(1-\gamma)}}{(1-\gamma)}=\frac{1}{1-\gamma}[P_2V_2-P_1V_1]=\frac{1}{\gamma - 1}[nRT_1-nRT_2]\\ \Rightarrow W=\left(\frac{nR}{\gamma-1}\right)(T_1-T_2)\\ \frac{nR}{\gamma-1}=\frac{nR}{\frac{C_p}{C_v}-1}=nR\frac{C_v}{C_p-C_v}=nR\frac{C_v}{R}=nC_v\\ \Rightarrow W = nCv(T_1-T_2)\]

然後之前的內能和定容關係式

\[\Delta U = nC_v (T_2-T_1)\]

的確以上兩個對比符合熱力第一定律(絕熱系統下$Q=0$)

\[\Delta Q = -W\]

比較

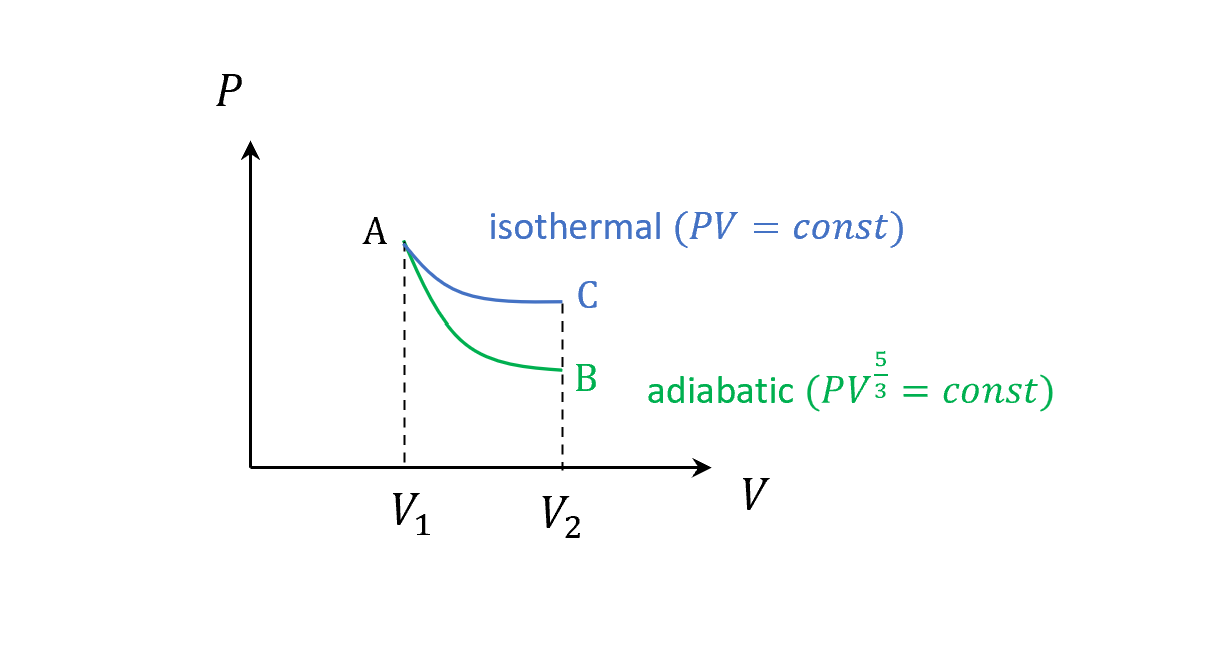
這裡畫個圖比較一下兩條曲線，注意一樣底下面積就是各自的做功