(8) 變分入門 ─ 運動方程與Lagrangian的關係是什麼？

從第二節和第五節都已經看到不論是要最小化某個物理量以滿足能量守恆，或是想要用近似方法在滿足運動方程解邊界問題的時候，結論都是要最小化這個物理量

\[\int_{0}^{T} \left(\frac{m}{2}\left(\frac{d\vec{r}}{dt}\right)^2-V(\vec{r})\right)\,dt=\int_{0}^{T}(KE-PE)\,dt\]

而括號中的形式，我們可以定為

\[L=KE-PE\]

就是大名鼎鼎的Lagrange function or Lagrangian for the particle.

現在我們正式用運動方程(EOM)再來推導一次，推導可以分成兩個方向

• EOM→Lagrangian (引入變分的概念)
• Lagrangian→EOM (利用變分求得運動方程)

從EOM推導Lagrangian

設真實軌跡為

\[x^*\]

EOM就是

\[-m\frac{d^2x^*}{dt^2} -\frac{\partial V}{\partial x^*} = 0\]

設

\[\delta x(t)\]

為真實軌跡的小小偏移量，如下圖

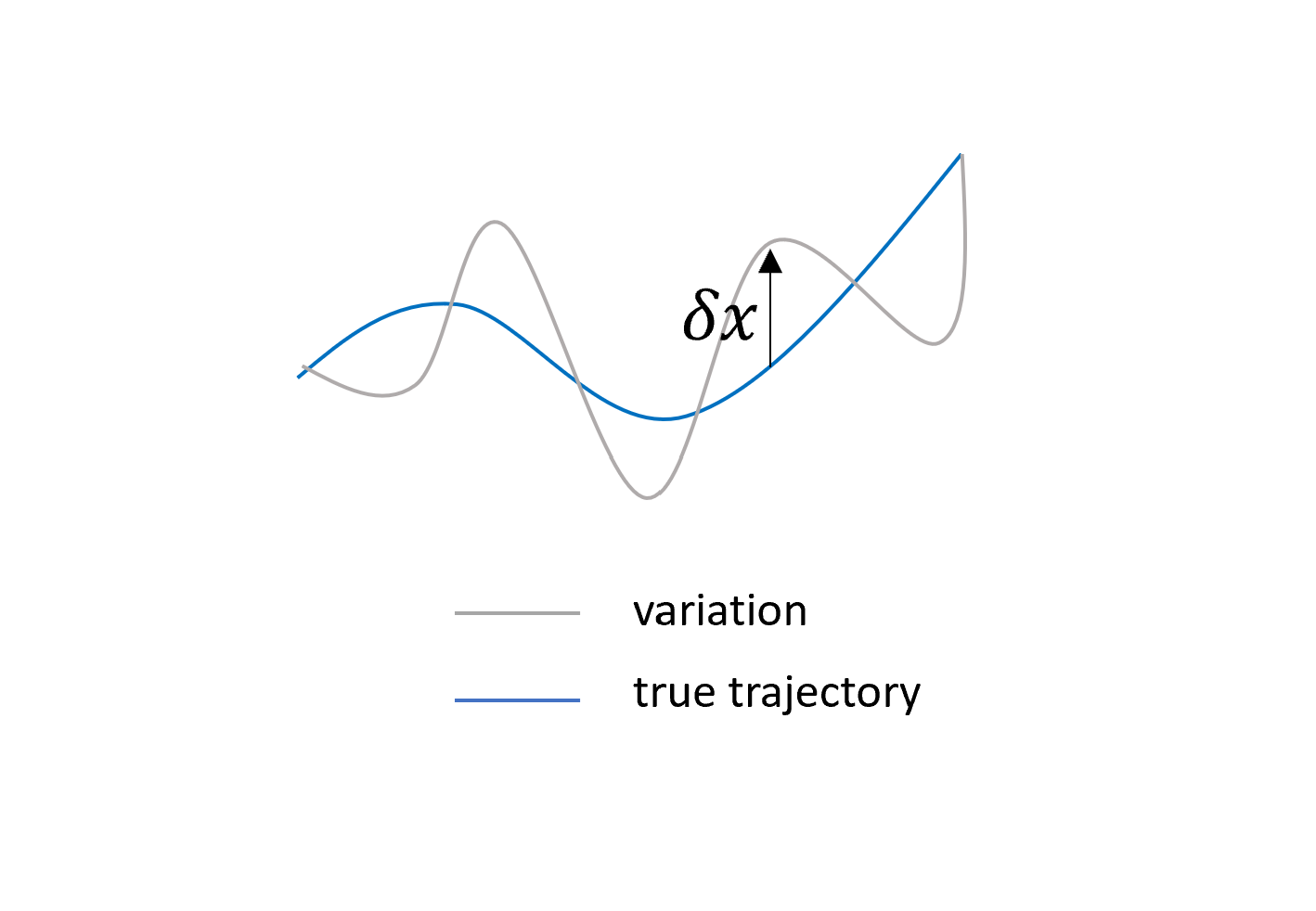
和EOM可以建構

\[\int_{0}^{T}\delta x\left(-m\frac{d^2x^*}{dt^2} -\frac{\partial V}{\partial x^*}\right)\,dt = 0\]

在進一步計算之前，先Note一下跟\(\delta\)有關的運算

Note：
- Varied trajectory $$ x\equiv x^*+ \delta x $$ - Calculus of derivative $$ \delta\left(\frac{1}{2}\left(\frac{dx}{dt}\right)^2\right) \equiv \frac{1}{2}\left(\frac{dx}{dt}\right)^2-\frac{1}{2}\left(\frac{dx^*}{dt}\right)^2 $$ $$ \fallingdotseq \frac{1}{2}\cdot 2 \cdot \frac{dx^*}{dt}\delta\left(\frac{dx}{dt}\right)=\frac{dx^*}{dt}\frac{d\delta x}{dt} $$ - Taylor expansion $$ V(x)=V(x^*+\delta x) = V(x^*)+\frac{\partial V}{\partial x^*}\delta x+\cdots $$ $$ \frac{\partial V}{\partial x^*}\delta x = V(x) - V(x^*) = \delta(V(x)) $$ - Changible $$ \delta\left(\frac{dx}{dt}\right)\equiv\frac{dx}{dt}-\frac{dx^*}{dt}=\frac{d}{dt}(x-x^*)=\frac{d\delta x}{dt} $$

那我們開始來算吧！

第一項：

\[\int_{0}^{T}\delta x(-m)\frac{d^2x^*}{dt^2}\,dt\]

分部積分

\[=-m\left(\delta x \frac{dx^*}{dt} \bigg|_{t=0}^{T} - \int_{0}^{T}\left(\frac{d\delta x}{dt}\frac{dx^*}{dt}\right)\, dt\right)\]

在邊界的變化量是零

\[\delta x(t=0)=\delta x(t=T)=0\]

所以

\[=m\int_{0}^{T}\left(\frac{d\delta x}{dt}\frac{dx^*}{dt}\right)\, dt\]

用Note第二項

\[=\frac{m}{2}\int_{0}^{T}\delta\left({\left(\frac{dx}{dt}\right)^2}\right)\, dt\] \[=\int_{0}^{T}\frac{m}{2}\left(\frac{dx}{dt}\right)^2\,dt - \int_{0}^{T}\frac{m}{2}\left(\frac{dx^*}{dt}\right)^2\,dt\] \[=\delta\int_{0}^{T}\frac{m}{2}\left(\frac{dx}{dt}\right)^2\,dt\]

第二項：

\[\int_{0}^{T}\delta x\left(-\frac{\partial V}{\partial x^*}\right)\,dt = 0\]

用Note第三項

\[=-\int_{0}^{T}\delta(V(x))\,dt\] \[=-\delta\int_{0}^{T}Vdt\]

整合

\[\int_{0}^{T}\delta x\left(-m\frac{d^2x^*}{dt^2} -\frac{\partial V}{\partial x^*}\right)\,dt = 0\] \[\Rightarrow \delta{\int_{0}^{T}\left(\frac{m}{2}\left(\frac{dx}{dt}\right)^2-V\right)\,dt}=0\] \[\Rightarrow \delta{\int_{0}^{T}L(x,\dot x)\,dt}=0\]

到這邊暫停一下，回顧我們之前對\(\delta\)的定義，是變化與真實之間的一點點「差」，若這個差為零，其實就是極值的概念，如同一個函數值，若往左走往右走，變化一下下，得出來的函數數值不變，那就代表是在這附近取極值！

這樣的結果也符合我們前言說的，L就是我們要最小化(取極值)的物理量！

從Lagrangian推導EOM

現在回來從Lagrangian推導回來，這次我們定廣義座標為q，包含變化量

\[q\equiv{q^*}+\delta{q}\]

另L我們也包含時間的變數(參考下節引入電磁場的公式)，所以更通用的Lagrangian定為\(L(q,\dot{q},t)\)。

取極值

\[0=\delta\int L(q,\dot{q},t)\,dt\] \[=\int\delta{L}(q,\dot{q},t)\,dt\] \[=\int\left(\frac{\partial L}{\partial q^*}\delta{q}+\frac{\partial L}{\partial \dot{q}^*}\delta{\dot{q}}\right)\,dt\]

這邊對t微分那項，在後面說明Conservation的時候會再提，這邊擷取一段Marion的說明，現階段就先不考慮time dependency

We saw in our pervious arguments that time is homogeneous within an inertial reference frame. Therefore, the Lagrangian that describes a closed system (i.e., a system not interacting with anything outside the system) cannot depend explicitly on time, that is

\[\frac{\partial L}{\partial t} = 0\]

─ (Thornton, S. T., & Marion, J.), Classical Dynamics of Particles and Systems, 5th edn, (p.260).

那繼續算

\[=\int\left(\frac{\partial L}{\partial q^*}\delta{q}+\frac{\partial L}{\partial \dot{q}^*}\frac{d}{dt}\delta{q}\right)\,dt\]

分部積分

\[=\int\left(\frac{\partial L}{\partial q^*}\delta{q}+\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}^*}\delta{q}\right)-\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}^*}\right)\delta{q}\right)\,dt\]

第二項因為邊界變化量是0

\[\because\delta{q}(t=0)=\delta{q}(t=T)=0\]

所以消掉剩

\[=\int_{0}^{T}\left(\frac{\partial L}{\partial q^*}-\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}^*}\right)\right)\delta{q}\,dt\]

總結看到

\[0=\delta\int L(q,\dot{q},t)\,dt=\int_{0}^{T}\left(\frac{\partial L}{\partial q^*}-\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}^*}\right)\right)\delta{q}\,dt\]

我們一開始是想要對L取極值，最後導向最右邊的式子，而因為\(\delta q\)是任意的(四面八方任意改變)微小變化量，所以大括號裡面要等於0：

\[\frac{\partial L}{\partial q^*}-\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}^*}\right)=0\] \[\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}^*}\right)=\frac{\partial L}{\partial q^*}\] \[\frac{\partial L}{\partial \dot{q}}\equiv p\equiv\text{generalized momentum}\] \[\frac{\partial L}{\partial {q}}\equiv\text{generalized force}\]

就是所謂的EOM了！

我們又稱 Euler-Lagrangian Euqation。

舉例

若

\[L=KE-PE=\frac{m}{2}\left(\frac{dx}{dt}\right)^2-V(x)\] \[\frac{\partial L}{\partial \dot{q}}=m\left(\frac{dx}{dt}\right),\quad \frac{\partial L}{\partial {q}}=\frac{\partial V}{\partial x}\] \[\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}}\right)=\frac{\partial L}{\partial q^*}\] \[\Rightarrow \frac{d}{dt}m\left(\frac{dx}{dt}\right)=\frac{\partial V}{\partial x}\] \[\Rightarrow m \frac{d^2 x}{dt^2}=\frac{\partial V}{\partial x}\]

就是F=ma。