(12) 變分對稱與守恆 ─ Lagrangian & Coordinate & Time
在Lagragian Form
\[\diff{}{t}\left(\pdv{L}{\dot{q_j}}\right)=\pdv{L}{q_j}\]從$L$對空間和時間的微分項,我們可以額外得出兩個不同的守恆量。
-
$\pdv{L}{q_j}=0 \quad\Rightarrow\pdv{L}{\dot{q_j}}=\text{const}$
-
$\pdv{L}{t}=0 \quad\Rightarrow\pdv{L}{\dot{q}}\dot{q}-L\equiv p\dot{q}-L=\text{const}$
對空間微分
如果$L$ 不是$q_j$的函數(not explicit function of $q_j$)
\[\pdv{L}{q_j}=0\]那麼
\[\pdv{L}{\dot{q_j}}\]就是一個守恆量。
證明
\[\diff{}{t}\left(\pdv{L}{\dot{q_j}}\right) = 0\\ p_j\equiv\pdv{L}{\dot{q_j}}=\text{constant value}\]舉例 - 角動量守恆
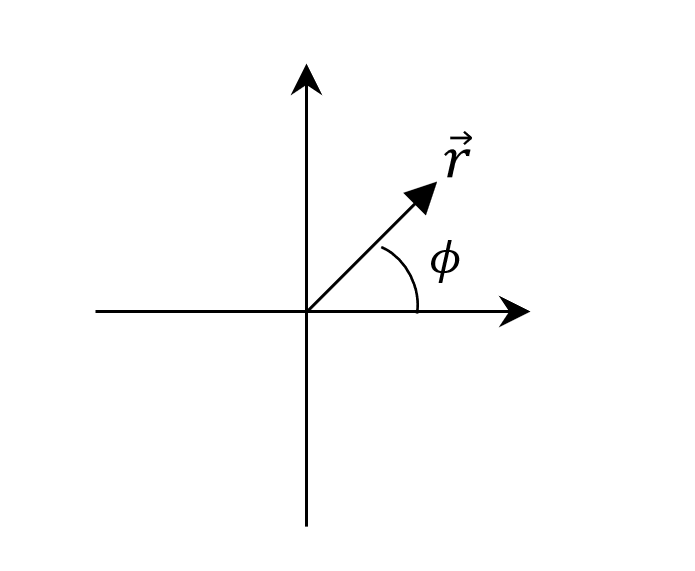
在二維極座標中,若位能不是角度的函數
\[V(\vec{r})=V(r)\]計算Lagriagin
\[\begin{align*} L = KE-PE = \frac{m}{2}(\dot{r}^2+r^2{\dot\phi}^2) - V(r)\\ \end{align*}\]對角度微分,動能本來就沒有,位能因為和角度無關,所以
\[\pdv{L}{\phi}=0\]因此守恆量
\[\begin{align*} \pdv{L}{\dot{\phi}}&= mr^2\dot{\phi} \\ &=\text{constant}\\ (r\dot{\phi} &= \text{tangential velocity}) \end{align*}\]即是角動量!
對時間微分
如果$L$ 不是$t$的函數(not explicit function of $t$)
\[\pdv{L}{t}=0\]那麼
\[p\dot{q}-L\equiv\pdv{L}{\dot{q}}\dot{q}-L\]就是一個守恆量。
證明
\[\begin{align*} &\diff{}{t}\left(\pdv{L}{\dot{q}}\dot{q}-L\right)\\ &=\diff{}{t}\left(\pdv{L}{\dot{q}}\dot{q}\right)+\pdv{L}{\dot{q}}\diff{}{t}\dot{q}-\left(\pdv{L}{q}\diff{q}{t}+\pdv{L}{\dot{q}}\diff{\dot{q}}{t}+\pdv{L}{t}\right)\\ &=\left(\diff{}{t}\pdv{L}{\dot{q}}-\pdv{L}{q}\right)\dot{q}-\pdv{L}{t}\\ &=0\cdot\dot{q}-\pdv{L}{t}\\ &=0\text{ (by assumtion }\pdv{L}{t}=0) \end{align*}\]得
\[\pdv{L}{\dot{q}}\dot{q}-L=\text{constant}\]舉例 - 能量守恆
\[L = \frac{m}{2}{\dot{\vv{r}}}^2-V(\vv{r})\]守恆量
\[\begin{align*} \pdv{L}{\dot{q}}\dot{q}-L&=m{\dot{\vv{r}}}\cdot{\dot{\vv{r}}}-\left(\frac{m}{2}{\dot{\vv{r}}^2}-V\right)\\ &=\frac{m}{2}{\dot{\vv{r}}}^2+V \end{align*}\]就是總能量(Total Energy)!
但這只能算是應用特例。
加上限制條件
如果我們加上限制條件$F(\vv{q})=0$(之後章節會細說),那有限制的Euler-Lagrange Equation
\[\begin{gather*} \diff{}{t}\pdv{L}{\dot{q}}=\pdv{L}{q}-\lambda\pdv{F}{q} \end{gather*}\]跟前面證明一樣我們來算
\[\begin{align*} \diff{}{t}\left(\pdv{L}{\dot{q}}\dot{q}-L\right)&=\left(\diff{}{t}\pdv{L}{\dot{q}}-\pdv{L}{q}\right)\dot{q}-\pdv{L}{t}\\ &=\left(-\lambda\pdv{F}{q}\right)\cdot\dot{q}-\pdv{L}{t}\\ &=-\lambda\diff{F}{t}-\pdv{L}{t}\\ &=-\pdv{L}{t}\\ &=0 \end{align*}\]假設是限制條件不會隨時間變動,所以一樣能得到
\[p\dot{q}-L\]仍然是守恆量。
