(11) 變分對稱與守恆 ─ Noether’s Theorem
Noether’s Theorem 主要是在說若一個系統有連續對稱性的時候,就會有對應的守恆量,在量力也成立。而這個概念也可以在Lagragian看出來。
首先我們先來看什麼是對稱性?就很像我們看一個球,轉了一點點(對稱性),仍然不變(不變量)。
從公式上來說就是將$L$做以下轉換,展開後在第一階仍相等:
\[L(\vec{q},\dot{\vec{q}},t)=L(\vec{q}+\epsilon\vec{w}(\vec{q}),\dot{\vec{q}}+\epsilon\dot{\vec{w}},t)\]其中$\epsilon$為任意微小量,$\vec{w}$為已知向量,代表$\vec{q}$移了一點,但Lagrange不變。
而這個守恆量對應不隨時間而改變的物理量就是
\[\frac{\partial L}{\partial\dot{\vec{q}}}\cdot\vec{w} = \text{an invariant}\\ = \text{constant of the motion(運動常數)}\]此即為 Noether’s theorem。
接下來我們用以下兩種來證明
- Euler-Langrange Equation
- Variational Principle
並舉三個例子對稱性和守恆量
- Translational symmetry: conservation of linear momentum
- Rotational symmetry: conservation of angular momentum
- Spiral symmetry: conservation of angular momentum and linear momentum
證明一:Euler-Langrange Euqation
展開到第一階
\[\begin{gather*} L(\vec{q},\dot{\vec{q}},t)=L(\vec{q}+\epsilon\vec{w},\dot{\vec{q}}+\epsilon\dot{\vec{\omega}},t)\\ \approxeq L(\vec{q},\dot{\vec{q}},t)+\frac{\partial L}{\partial \vec{q}}\cdot\epsilon\vec{w}+\frac{\partial L}{\partial \dot{\vec{q}}}\cdot\epsilon\dot{\vec{w}}\\ \Rightarrow\frac{\partial L}{\partial \vec{q}}\cdot\vec{w}+\frac{\partial L}{\partial \dot{\vec{q}}}\cdot\dot{\vec{w}}=0 \end{gather*}\]注意這個$\epsilon$展開不是近似解,是Exact的解,代表
\[\begin{gather*} f(x)=f(x+\epsilon) \text{ up to } O(\epsilon)\\ f'(x)=0\text{ for all x} \end{gather*}\]By Euler-Lagrange:
\[\begin{gather*} \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\vec{q}}}\right)=\frac{\partial L}{\partial \vec{q}}\\ \Rightarrow \vec{w}\cdot\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\vec{q}}}\right)=\vec{w}\cdot\frac{\partial L}{\partial \vec{q}}=-\frac{\partial L}{\partial \dot{\vec{q}}}\cdot\dot{\vec{w}}\\ \Rightarrow \vec{w}\cdot\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\vec{q}}}\right)+\dot{\vec{w}}\cdot\frac{\partial L}{\partial \dot{\vec{q}}}=0\\ \Rightarrow\frac{d}{dt}\left(\vec{w}\cdot\frac{\partial L}{\partial \dot{\vec{q}}}\right)=0 \end{gather*}\]得證
\[\frac{\partial L}{\partial\dot{\vec{q}}}\cdot\vec{w} = \text{constant}\]證明二:Variational Principle
因為Euler-Lagrange也是從Variational principle來的,所以我們直接存最原始的變分原理出發:
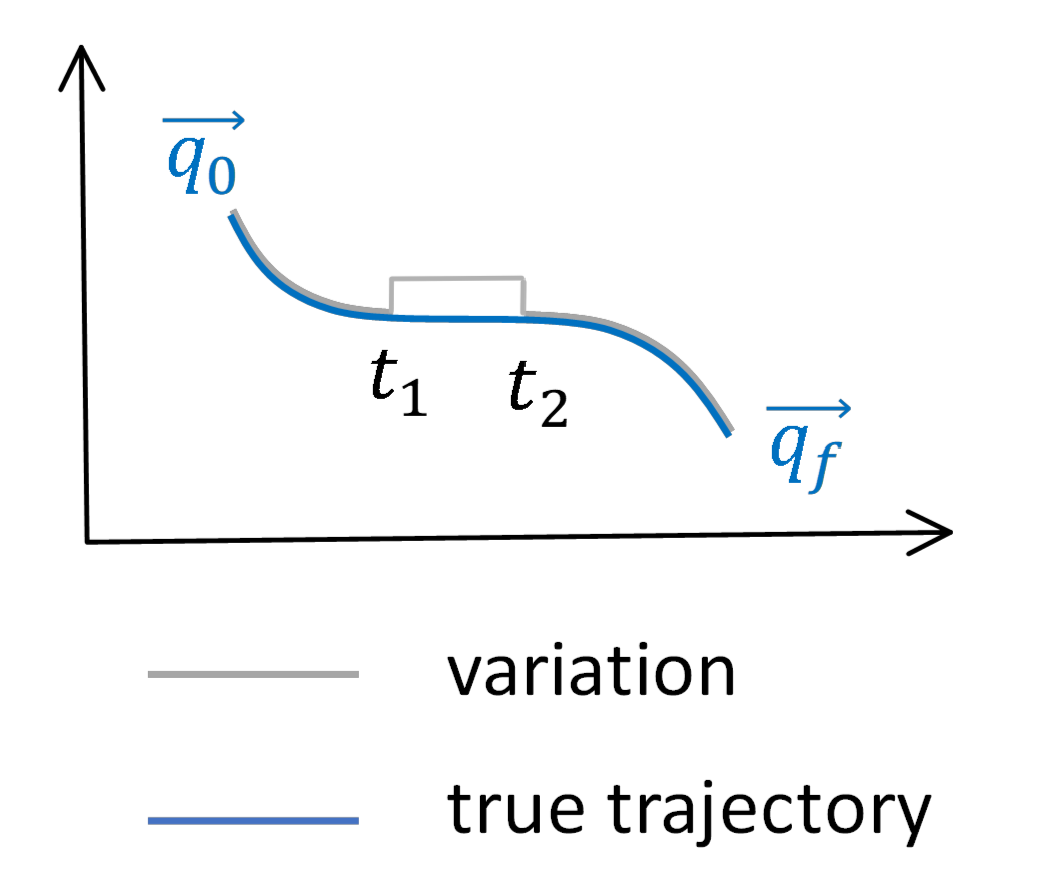
先定
\[\vec{w}\equiv\text{ direction of symmetry, "generator" of the symmetry} \\ \theta\equiv\text{ kronecker delta }\] \[\theta(\xi)\equiv \left\{ \begin{array}{ll} 1, \text{ if } \xi \geq{0}\\ 0, \text{ if } \xi <{0} \end{array} \right. , \frac{d\theta(\xi)}{d\xi}=\delta(\xi)\]所以變化的軌跡
\[\begin{gather*} q(t)\equiv q^*+\epsilon\vec{w}(\vec{q})(\theta(t-t_1)-\theta(t-t_2))\\ \end{gather*}\]變化差值
\[\begin{gather*} \delta{q}\equiv\text{grey line - blue line}\\ \delta{q}\equiv\epsilon{w}(\theta(t-t_1)-\theta(t-t_2))\\ \delta\dot{q}=\frac{d\delta{q}}{dt}=\epsilon\frac{dw}{dt}(\theta(t-t_1)-\theta(t-t_2))+\epsilon{w}(\delta(t-t_1)-\delta(t-t_2)) \end{gather*}\]這時候就來用變分的概念啦!希望做一點點的改變的時候,還是一樣的(取極值),所以想要求
\[\begin{align*} 0&=\int_{\text{grey line}}^{}L\,dt - \int_{\text{blue line}}^{}L\,dt=\delta\int_{}^{}L\,dt\\ &=\int_{}^{}\delta{L}\,dt\\ &=\int_{}^{}\left(\pdv{L}{q}\cdot\delta{q}+\pdv{L}{\dot{q}}\cdot\delta\dot{q}\right)\\ &=\int_{}^{}\pdv{L}{q}\epsilon{w}(\theta(t-t_1)+\theta(t-t_2))\\ &\quad+\pdv{L}{\dot{q}}\epsilon\diff{w}{t}(\theta(t-t_1)-\theta(t-t_2))\\ &\quad+\pdv{L}{\dot{q}}\epsilon{w}(\delta(t-t_1)+\delta(t-t_2))\,dt \end{align*}\]因為對稱性
\[\begin{gather*} L(q^*, \dot{q}^*,t) = L(q^*+\epsilon{w}, \dot{q}^*+\epsilon{\dot{w}},t)\\ \Rightarrow\pdv{L}{q^*}\epsilon{w}+\pdv{L}{\dot{q}^*}\epsilon\dot{w}=0\\ \Rightarrow\pdv{L}{q^*}{w}+\pdv{L}{\dot{q}^*}\dot{w}=0 \end{gather*}\]以及$\delta$ function的特性
\[\begin{gather*} \int_{}^{}f(\vv{\xi})\delta(\xi-a)\,d\xi=f(a))\text{ whenever the domain of intergration includes }\xi = a \end{gather*}\]所以推導繼續
\[\begin{gather*} =\epsilon\int_{}^{}\pdv{L}{\dot{q}}{w}\left(\delta(t-t_1)+\delta(t-t_2)\right)\,dt\\ =\epsilon\left(\pdv{L}{\dot{q}}w \bigg |_{t=t_1}^{}-\pdv{L}{\dot{q}}w \bigg|_{t=t_2}^{}\right)=0 \end{gather*}\]代表$t_1$和$t_2$不同時間時,都沒有變,故而得到一樣的結果,得證
\[\Rightarrow\pdv{L}{\dot{q}}\cdot{w} = \text{constant}\]舉例一:Translational Symmetry
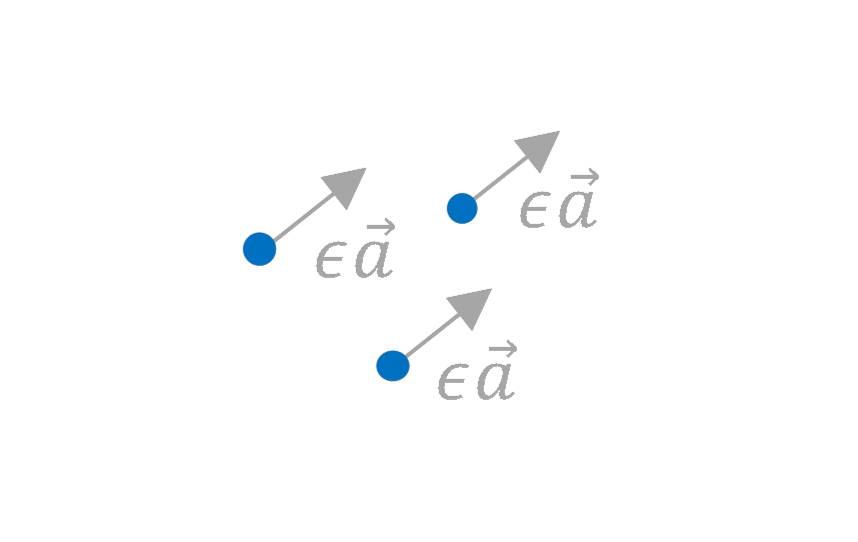
假設N-particle系統中每一個小點都移動一點點
\[\left\{ \begin{array}{ll} \vv{q}\equiv(\vv{r}_1,\vv{r}_2,\cdots,\vv{r}_n)\\ \vv{w}\equiv(\vv{a},\vv{a},\cdots,\vv{a}) \end{array} \right.\]設位能只跟彼此有關係
\[V(\vv{r}_1,\vv{r}_2,\cdots,\vv{r}_n) \text{ depends only on }\|\vv{r}_j-\vv{r}_k\| \text{ where j, k = 1,...,n}\]所以移動的這一小點會維持不變性
\[\vv{r}_j\rightarrow\vv{r}_j+\epsilon\vv{a} \text{ makes L invariant}\]計算Lagragian
\[\begin{align*} L &\equiv \frac{m_1}{2}{\dot{\vec{r}}_1}^2+\frac{m_2}{2}{\dot{\vec{r}}_2}^2+\cdots-V(\vv{r}_1,\cdots,\vv{r}_n)\\ \vv{w}\cdot\pdv{L}{\dot{\vec{q}}} &= \vv{a}\cdot\pdv{L}{\dot{\vec{r}}_1}+\vv{a}\cdot\pdv{L}{\dot{\vec{r}}_2}+\cdots+\vv{a}\cdot\pdv{L}{\dot{\vec{r}}_n}\\ &=\vv{a}\cdot{m_1}\dot{\vec{r}}_1+\vv{a}\cdot{m_2}\dot{\vec{r}}_2+\cdots+\vv{a}\cdot{m_n}\dot{\vec{r}}_n\\ &=\vv{a}\cdot\left(\sum_{j}^{}{m_j}{\dot{\vec{r}}}_j\right)\\ &=\text{constant} \end{align*}\]得出來的就是在有連續對稱性的情況下,不隨時間改變的物理量(沿著$\vv{a}$方向的總線動量 the total linear momentum along the direction of $\vv{a}$)對應的就是我們熟知的線動量守恆!
舉例二:Rotational Symmetry
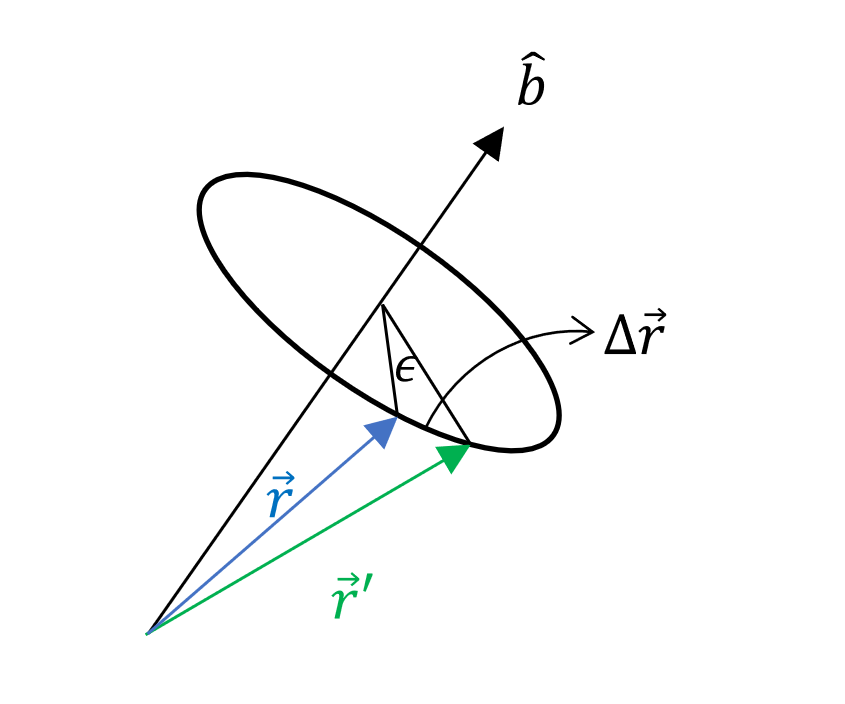
現在假設一個沿著$\vec{b}$(unit vector)方向旋轉時仍有轉動對稱性質
\[\left\{ \begin{array}{ll} \vv{q}\equiv(\vv{r}_1,\vv{r}_2,\cdots,\vv{r}_n)\\ \vv{w}\equiv(\hat{b}\times\vv{r}_1, \hat{b}\times\vv{r}_2, \cdots ,\hat{b}\times\vv{r}_n) \end{array} \right.\]轉動一點維持不變性
\[\vv{r}_j\rightarrow\vv{r}_j+\epsilon\hat{b}\times\vv{r}_j\]計算Lagragian
\[\begin{align*} L &\equiv \frac{m_1}{2}{\dot{\vec{r}}_1}^2+\frac{m_2}{2}{\dot{\vec{r}}_2}^2+\cdots-V(\vv{r}_1,\cdots,\vv{r}_n)\\ \vv{w}\cdot\pdv{L}{\dot{\vec{q}}} &=(\hat{b}\times\vv{r}_1)\cdot(m_1\dot{\vv{r}}_1)+(\hat{b}\times\vv{r}_2)\cdot(m_2\dot{\vv{r}}_2)+\cdots+(\hat{b}\times\vv{r}_n)\cdot(m_n\dot{\vv{r}}_n)\\ &=\left(\sum_{j}^{}(m_j\vv{r}_j\times\dot{\vv{r}}_j)\cdot\hat{b}\right)\\ &=\text{constant} \end{align*}\]得出來的就是在有連續對稱性的情況下,不隨時間改變的物理量(沿著$\hat{b}$方向的總角動量 the total angular momentum along the direction of $\hat{b}$)對應的就是我們熟知的角動量守恆!
舉例三:Spiral symmetry
現在定圓柱座標$(\rho, \phi, z)$
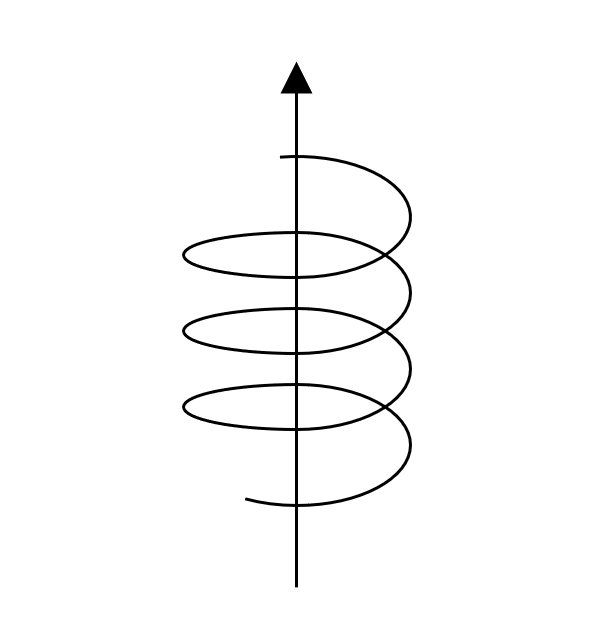
我們繞一點角度,往上走一點點,和在低一點的地方看也會是一樣的,所以
\[\vv{w}=(0,1,c)\]可以維持不變性
\[(\rho, \phi, z) \rightarrow(\rho,\phi+\epsilon,z+\epsilon c)\]計算Lagragian
\[\begin{align*} L=KE-PE&\equiv\frac{m}{2}\left({\dot\rho}^2+\rho^2{\dot\phi}^2+{\dot{z}}^2\right)-V\\ \vv{w}\cdot\pdv{L}{\dot{\vv{q}}}&=\frac{m}{2}\rho^2\cdot{2\dot\phi}\cdot{1}+\frac{m}{2}\cdot{2}\cdot\dot{z}\cdot{c}\\ &=m\rho^2\dot\phi+m\dot{z}\cdot{c}\\ &=\text{constant} \end{align*}\]這兩項分別是隨著z方向的角動量和線動量,所以得出來一樣在有對稱性的情況下,這個不隨時間改變的物理量對應就是角動量和線動量守恆!
