(14) 變分條件 ─ Holonomic & non-Holonomic Constraints
當我們在解一問題的時候,或多或少會遇到一些限制,譬如說一個轉盤只能在特定斜坡上轉下來,或是有其他已知的系統限制條件,代表我們對這個系統了解很多,對資訊掌握得很好。
接下來我們看要怎麼進一步表述這個問題。
Holonomic Constraints
設有一個N度空間(Configuration Space),Generalized座標用$q_1 - q_N$表示。
若我們知道現在解的運動問題有一個限制條件
\[F(q_1,q_2,\cdots,q_N)=0\]代表這個運動在高度空間裡面只能在這個 Hypersurface $F$ 運動,
我們稱其為 Holonomic Constraints。
舉例來說$F(x,y,z)=0$就是對應一個曲面,我們限制只能在這個曲面上運動,所以幾乎很多在Congiruation Space的點都到不了,運動地很死,是一種Global的限制。
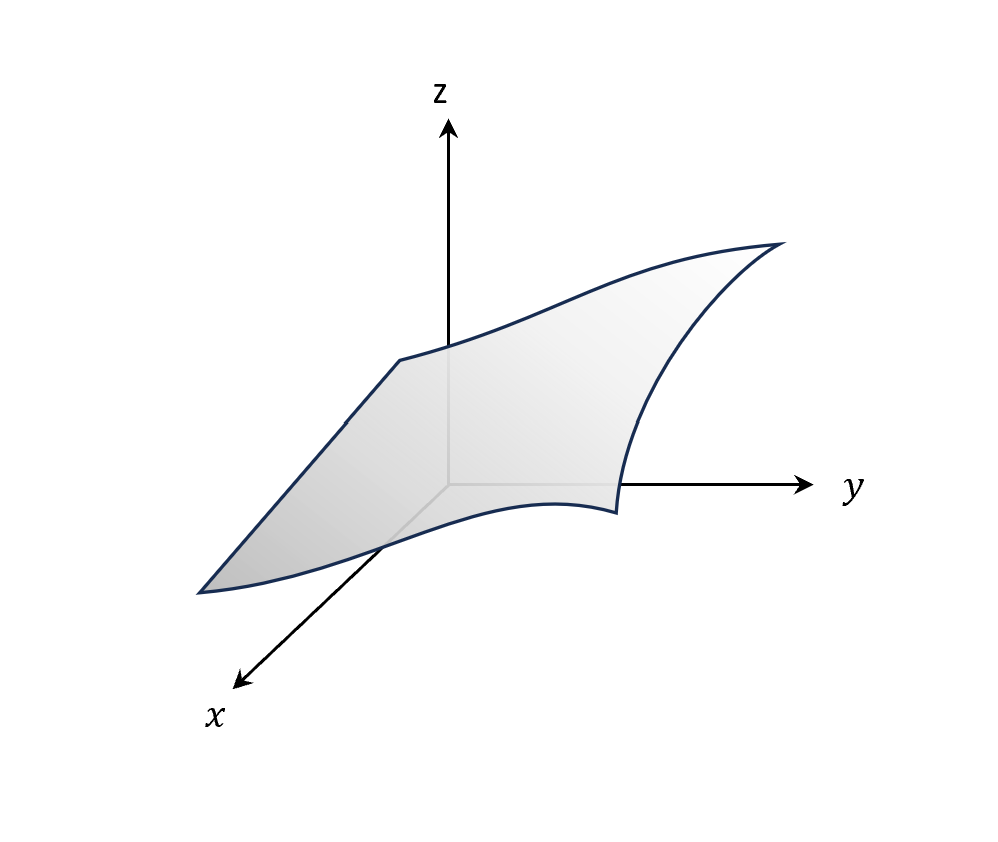
困難點
但實際上,我們很難一開始就知道要把限制寫成這樣的形式,無法馬上就寫出Globally Holonomic Constraint,但在Local時,我們可以寫出微分形式的限制(differential form constraint),就是在$q$的位置走出去$(d\vec{q})$,但不是任意方向都可以走,必須遵循當下局部的向量場$\vec{f}$
\[\vec{f}\cdot{d}\vec{q}=0\\ \Rightarrow f_1(q_1,\cdots,q_N)dq_1+f_2(q_1,\cdots,q_N)dq_2+\cdots+f_N(q_1,\cdots,q_N)dq_N=0\]
所以我們接下來要確定的是,雖然我們通常一時之間無法看出$F(\vec{q})=0$的形式,但微分形式也許能對應得到。
重新定義問題
當給定
\[\vec{f}\cdot{d}\vec{q}=0, \quad \vec{f}=\vec{f}(\vec{q})\]是否能對應到Holomonic Constraint?
驗證方法
我們把Holonomic Constraint化成differential form,看有沒有差別。
設Holonomic Constraint
\[F=0\]因為$dq$不論怎麼走,$F$數值都不變,都在這個contraint上,所以
\[0=dF=d\vec{q}\cdot\nabla{F}\]得
\[\nabla{F}\perp d\vec{q}\]發現和
\[\vec{f}\cdot{d}\vec{q} = 0\\ \Rightarrow \vec{f}\perp{d}\vec{q}\]是一樣的形式。
因此若給定的微分形式constraint要能對應Holonomic,則一定滿足
這個正比的factor取決於我們在configuration space的哪個點。
有解了?
看起來微分形式真的能對應到Holonomic Constraint,但這樣就解決我們的問題了嗎?
No!
這仍然是一個很難的問題,你想$\vec{f}$是我們自己提供的,卻要找未知的$F$和未知的factor來符合此方程式。
聽起來就還是很困難的問題。
如何確定是不是Holonomic Constraint?走走看唄~
不過好處是,這個對應關係還是在的,所以我們換個解決的想法:
如果$F$真的存在,那麼用已知的特性先走走看(walking around),就仍然不會走出這個Hypersurface(無法逃出這個限制的手掌心)。
想像一下在杯蓋上面走來走去,會有可能走上來0.1公分嗎?如果怎麼走都走不到,那就是Holonomic Constraint,反之若能夠證明走上來,就代表是non-Holonomic!

之所以要亂走一下,不能一步登天,是因為還被微分形式限制住。另外數學上也不用走那麼遠,基本上就走一圈回來,看能不能走出去就能判定是否是Holonomic。
走一圈的公式表示
給定
\[\vec{f}\cdot{d}{\vec{q}}=0\\ \Rightarrow f_1dq_1+\cdots+f_Ndq_N=0\]現在找N-1個 independent vectors
\[\vec{e}_1, \cdots, \vec{e}_{N-1}\]也皆正交於 $\vec{f}\in\mathbb{R}^N$。(我的想法是{$\vec{e}_j$}可以等價於$dq$的意思。)
如果要是Holonomic Constraint,那麼{$\vec{e}_j$}就會是Hypersurface ($F(\vec{q})=0$)的切線向量。並且在此平面上,任何時刻走的切線向量都會是{$\vec{e}_j$}的線性組合。
所以當我們設法走一圈回來$\alpha\vec{e}_1\rightarrow\beta\vec{e}_2\rightarrow(-\alpha\vec{e}_1)\rightarrow(-\beta\vec{e}_2)$
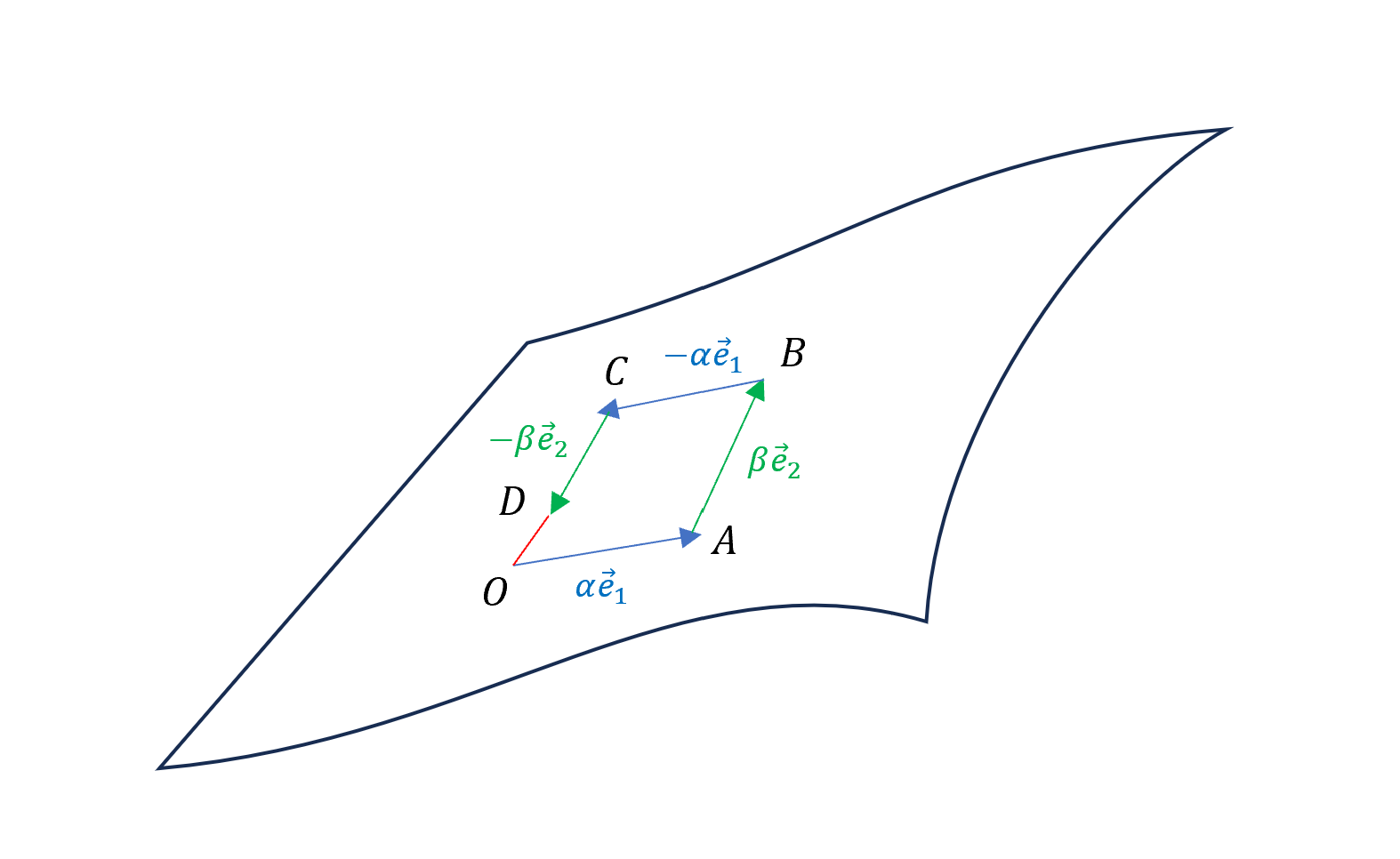
就要看回來時的$\overline{OD}$還是不是{$\vec{e}_j$}的線性組合,是的話則代表還在此Hypersurface上,是Holonomic Constraint。
注意$\alpha$和$\beta$都是很小的量,並且每個點的$\vec{e}_1$和$\vec{e}_2$都不一樣(不是真正的座標網格,會隨空間不同),所以走一圈回來不一定回到原點,$\overline{OD}$不一定會是0,但因為還是很接近,會是$\alpha\times\beta$的數量級。
那怎麼計算$\overline{OD}$呢?
還記得我們都學過
\[\nabla_{\vec{v}}\vec{u}\equiv\text{directional derivative of }\vec{u}\text{ along the vector }\vec{v}\]所以
\[\overline{OD}=\alpha\beta(\nabla_{\vec{e}_1}\vec{e}_2-\nabla_{\vec{e}_2}\vec{e}_1)\]代表$\vec{e}_2$在$\vec{e}_1$方向的差和$\vec{e}_1$在$\vec{e}_2$方向的差。
再由我們前面說的(正式來說是Frobenius Integrability Criterion),總結現在只要確認
是的話,會在Hypersurface上存在,就是Holonomic Constraint。
舉例
講這麼多,直接舉個例子吧!
假設我們現在已知並定
求
\[\begin{align*} \nabla_{\vec{e}_1}\vec{e}_2-\nabla_{\vec{e}_2}\vec{e}_1&=\left[\nabla_{\hat{e}_x}(\hat{e_y}+x\hat{e}_z)\right]-\left[\nabla_{\hat{e_y}+x\hat{e}_z}(\vec{e}_1)\right]\\ &=\left[\nabla_{\hat{e}_x}(\hat{e_y}+x\hat{e}_z)\right]-\left[\nabla_{\hat{e}_y}{\vec{e}_1}+\nabla_{x\hat{e}_z}\vec{e}_1\right]\\ &=\left[\nabla_{\hat{e}_x}(\hat{e_y}+x\hat{e}_z)\right]-\left[\nabla_{\hat{e}_y}{\vec{e}_1}+x\nabla_{\hat{e}_z}\vec{e}_1\right]\\ &=\left[\pdv{}{x}(\hat{e}_y+x\hat{e}_z)\right]-\left[\pdv{\vec{e}_1}{y}+x\pdv{\vec{e}_1}{z}\right]\\ &=\left[\hat{e}_z\right]-\left[\vec{0}+x\vec{0}\right]\\ &=\hat{e}_z \end{align*}\]確認是不是${\vec{e}_k}$的線性組合
\[\begin{align*} \hat{e}_z\stackrel{?}{=}&C_1\vec{e}+C_2\vec{e}_2\\ =&C_1\hat{e}_x+C_2(\hat{e}_y+x\hat{e}_z)\\ =&C_1\hat{e}_x+C_2\hat{e}_y+C_2x\hat{e}_z \end{align*}\]從$x$和$y$項看出至少$C_1 = 0, \quad C_2 = 0$,但這樣$z$項也被消掉了!
所以得出
\[\nabla_{\vec{e}_1}\vec{e}_2-\nabla_{\vec{e}_2}\vec{e}_1=\hat{e}_z\neq \{\vec{e}_k\}\]不是${\vec{e}_k}$的線性組合,所以不是Holonomic Constraint!
補個圖就可以更清楚哩!
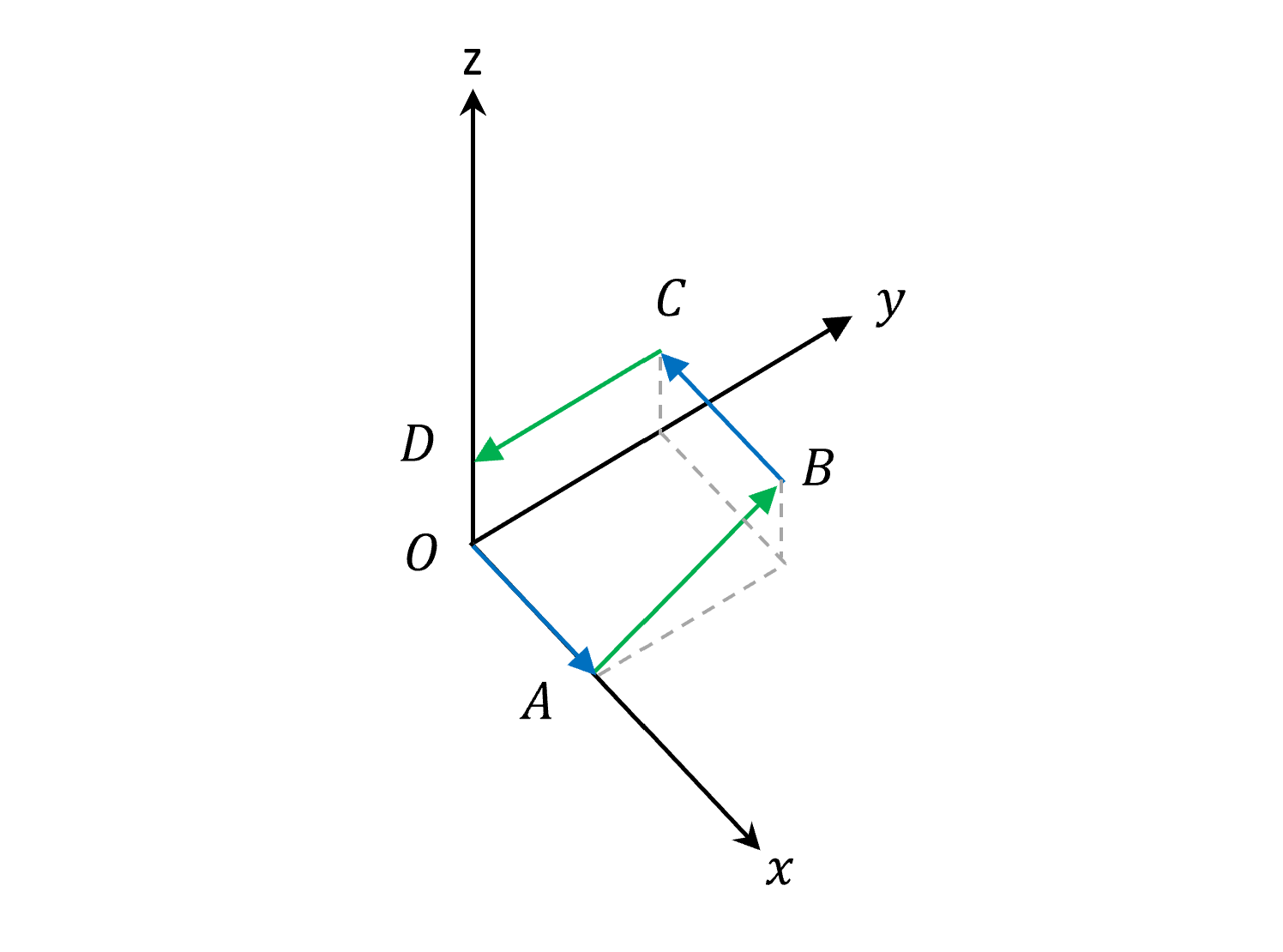
不過我們現在有點偷吃步,舉例直接從給定${\vec{e}_k}$出發來證明,實際上應該是先給定一個$\vec{f}$,然後自己去造${\vec{e}_k}$,再用上面的方式來證明是不是屬於Holonomic Constraint。
進一步地說,我們反推假設現在知道微分形式的
\[\vec{f}=(0,-x,1) = 0\hat{e}_x-x\hat{e}_y+\hat{e}_z\]造的${\vec{e}_k}$滿足$\vec{f}\perp{\vec{e}_1},\vec{e}_2$
\[\left\{ \begin{array}{ll} \vec{f}\cdot\vec{e}_1=0\\ \vec{f}\cdot\vec{e}_2=-x+x = 0 \end{array} \right.\]但因為
\[\nabla_{\vec{e}_1}\vec{e}_2-\nabla_{\vec{e}_2}\vec{e}_1\neq \{\vec{e}_k\}\]所以
\[\vec{f}\cdot d\vec{q}=0\cdot dx-x\cdot dy+\cdot dz=0\]就是non-Holonomic Constraint。
Holonomic vs non-Holonomic
到此,算是把想講的都講完了,但是這只是在講解法的精神,實作上,其實有更簡單的作法,不需要去找$\vec{e}_1,\vec{e}_2$,只要確認
\[\vec{f}\cdot(\nabla\times\vec{f})\stackrel{?}{=}0\]就好哩!
證明(Frobenius Criterion)
選擇一組正交歸一單位向量$\vec{e}_1,\vec{e}_2$
現在來求
\[\begin{align*} \vec{f}\cdot(\nabla_{\vec{e}_1}\vec{e}_2-\nabla_{\vec{e}_2}\vec{e}_1)&=\left[\nabla_{\vec{e}_1}(\vec{f}\cdot{\vec{e}_2})-\vec{e}_2\cdot\nabla_{\vec{e}_1}\vec{f}\right]-\left[\nabla_{\vec{e}_2}(\vec{f}\cdot{\vec{e}_1})-\vec{e}_1\cdot\nabla_{\vec{e}_2}\vec{f}\right]\\ &=\left[0-\vec{e}_2\cdot\nabla_{\vec{e}_1}\vec{f}\right]-\left[0-\vec{e}_1\cdot\nabla_{\vec{e}_2}\vec{f}\right]\\ &=-\vec{e}_2\cdot\nabla_{\vec{e}_1}\vec{f}+\vec{e}_1\cdot\nabla_{\vec{e}_2}\vec{f} \end{align*}\]套用Local Cartesian座標系統,使得$\vec{e}_1,\vec{e}_2,\vec{f}$對應$\hat{e}_x,\hat{e}_y,$(some number)$\cdot\hat{e}_z$
因此定
\[\vec{f}\equiv\hat{e}_x{f_x}+\hat{e}_y{f_y}+\hat{e}_z{f_z}\]則
\[\begin{align*} {\vec{f}}\cdot(\nabla_{\vec{e}_1}\vec{e}_2-\nabla_{\vec{e}_2}\vec{e}_1)&=-\vec{e}_2\cdot\nabla_{\vec{e}_1}\vec{f}+\vec{e}_1\cdot\nabla_{\vec{e}_2}\vec{f}\\ &=-\hat{e}_y\cdot\pdv{}{x}\vec{f}+\hat{e}_x\cdot{\pdv{}{y}\vec{f}}\\ &=-\pdv{f_y}{x}+\pdv{f_x}{y}\\ &\propto\hat{e}_z\cdot(\nabla\times{\vec{f}})\\ &\propto\vec{f}\cdot(\nabla\times{\vec{f}}) \end{align*}\]所以只要算旋度就好啦!
總結
-
Holonomic Constraint:$\vec{f}\cdot(\nabla\times\vec{f})=0$
怎麼都爬不出來。
-
non-holonomic Constraint:$\vec{f}\cdot(\nabla\times\vec{f})\neq{0}$
拐個彎繞一繞就出來了!
