(15) 變分條件 ─ Lagragian Multiplier
現在有一個簡單且基本的微積分問題:
找一個點$\vec{q}\in\mathbb{R}^N$,使得 $G(\vec{q})$ 為極值,並限制 $\vec{q}$ 滿足條件$H(\vec{q})=0$。
一般來說找極值,就是對每個維度$(q_1\cdots{q_N})$作微分,找到都為零的就是極值,但因為現在有限制條件,所以不能這樣直接做,要再換個方法。
Let’s go!
解有限制條件的極值問題
假設$\vec{q^*}$為極值的點,$d\vec{q}$為微小的偏移量,因為限制條件恆成立,所以必定滿足
\[H(\vec{q^*}+d\vec{q})-H(\vec{q^*})=0\\ \Rightarrow d\vec{q}\cdot\nabla{H^*}=0\]再來因為本身不會有任何增減量才會是極值,所以
\[G(\vec{q^*}+d\vec{q})-G(\vec{q^*})=0\\ \Rightarrow d\vec{q}\cdot\nabla{G^*}=0\]結合以上兩種,從幾何角度上來看,代表對所有$d\vec{q}$會滿足
\[d\vec{q}\perp\nabla{H^*} (\text{ some vector in }\mathbb{R}^N)\nonumber\\ d\vec{q}\perp\nabla{G^*} (\text{ some vector in }\mathbb{R}^N)\nonumber\\\]兩者成正比關係
\[\nabla{G^*}\propto\nabla{H^*}\nonumber\\ \nabla{G^*} - \lambda\nabla{H^*} = 0\]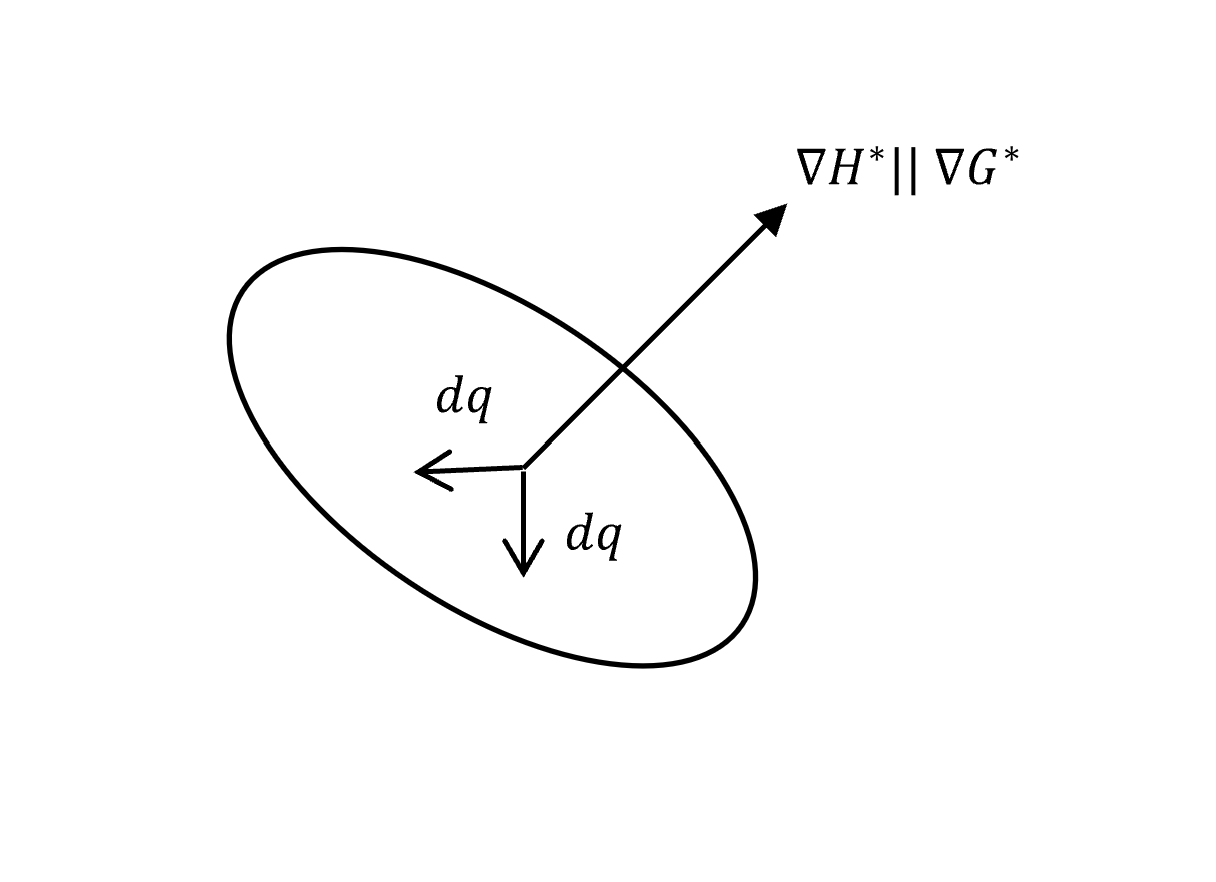
這個$\lambda$,我們就稱為 undetermined multiplier。
若找到的$\vec{q}$不滿足$\nabla G^* - \lambda\nabla H^* $ 則$\vec{q}$點就不會是極值。
Euler-Lagrange Equation with Constraints
現在我們把這個限制條件套回Euler-Lagrange Equation,但在此之前,一樣先問個簡單的問題:
若知
\[\int_{0}^{T}\vec{g}(t)\cdot\delta\vec{q}(t)\,dt=0\]且變化量$\delta{q}(t)$有限制條件
\[\int_{0}^{T}\vec{h}(t)\cdot\delta\vec{q}(t)\,dt=0?\]要怎麼求這裡的$\vec{g}$?
感覺是不是和之前推導Euler-Lagrange Equation很像?從求$L$的極值出發 $$ 0=\delta\int L(q,\dot{q},t)\,dt=\int_{0}^{T}\left(\frac{\partial L}{\partial q^*}-\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}^*}\right)\right)\delta{q}\,dt $$
不過我們先撇開不談,回到原本問題,若知道兩個函數$\vec{u}(t)$和$\vec{v}(t)$內積可以表示
\[{\left\langle \vec{u} \; \vert \; \vec{v} \right\rangle}\equiv\int_{0}^{T}\vec{u}(t)\cdot\vec{v}(t)\, dt\](這裡算是mixed的內積,把finite component space和函數無限維的積分一起看。)
所以最前面的問題就變成是
\[\left\{ \begin{array}{ll} {\left\langle \vec{g} \; \vert \; \delta\vec{q} \right\rangle}=0\\ {\left\langle \vec{h} \; \vert \; \delta\vec{q} \right\rangle}=0 \end{array} \right.\]得
\[\vec{g}{\quad\mathbin{\!/\mkern-5mu/\!}\quad}\vec{h}\]再結合本文最前面的undetermined multiplier,就可以寫成
\[\vec{g}-\lambda\vec{h} =0\]若有多條限制
\[\left\{ \begin{array}{ll} \int_{0}^{T}\vec{h}^{(1)}\cdot\delta\vec{q}\,dt=0\\ \int_{0}^{T}\vec{h}^{(2)}\cdot\delta\vec{q}\,dt=0\\ \vdots\\ \int_{0}^{T}\vec{h}^{(n)}\cdot\delta\vec{q}\,dt=0 \end{array} \right.\]內積幾何上就是
\[\left\{ \begin{array}{ll} {\left\langle \vec{h}^{(1)} \; \vert \; \delta\vec{q} \right\rangle}=0\\ {\left\langle \vec{h}^{(2)} \; \vert \; \delta\vec{q} \right\rangle}=0\\ \vdots\\ {\left\langle \vec{h}^{(n)} \; \vert \; \delta\vec{q} \right\rangle}=0 \end{array} \right.\]總結在一起就是
\[\vec{g}-\lambda_1\vec{h}^{(1)} - \lambda_2\vec{h}^{(2)} - \cdots - \lambda_n\vec{h}^{(n)} =0\]移項得解答
\[\vec{g} = \lambda_1\vec{h}^{(1)} + \lambda_2\vec{h}^{(2)} + \cdots + \lambda_n\vec{h}^{(n)}\]落在被限制過的組合空間裡。
進一步看限制條件
不過我們說有多個限制條件是什麼意思?實際上當碰到限制條件
\[\vec{f}(t)\cdot\delta\vec{q}(t)=0 \text{ for all } t \in [0,T]\]其實就隱含了無限多個條件(看時間怎麼切割),因為任何時刻的條件都要符合。
我們可以借用Dirac’s delta表示法
這樣t只是一個label of imposed constraints,可以是任意數值落在$[0,T]$的區間。
所以一樣,我們現在維持
\[{\left\langle \vec{g} \; \vert \; \delta\vec{q} \right\rangle}=0\]$\delta\vec{q}$需要滿足的限制條件為
\[\int_{0}^{T}\left(\delta(t-\tau)\vec{f}(\tau)\cdot\delta\vec{q}(\tau)d\tau\right)=0\\ {\left\langle \delta(t-\tau)\vec{f} \; \vert \; \delta\vec{q}\right\rangle}=0\]所以解就是
\[\vec{g}-\int_{0}^{T}\lambda_t\delta(t-\tau)\vec{f}(\tau)d\tau=0\\ \Rightarrow\vec{g}-\lambda_t\vec{f}(t) = 0\]$\lambda_t$現在就是跟$t$有關的函數了!
最後回到我們的Euler-Lagrange Equation
當要求$L(q,\dot{q},t)$極值,並且限定於條件
\[\begin{gather*} f_1(\vec{q})\delta{q_1}+f_2(\vec{q})\delta{q_2}+\cdots+f_n(\vec{q})\delta{q_n}\equiv\vec{f}\cdot\delta{q}=0\\ q\equiv(q_1,q_2,\cdots,q_n)\equiv\vec{q} \end{gather*}\]真正的解$ q^* $就會滿足
\[\diff{}{t}\pdv{L}{\dot{\vec{q}}^*}-\pdv{L}{\vec{q}^*}-\lambda(t)\vec{f}(\vec{q}^*)=0\\ \Rightarrow\diff{}{t}\pdv{L}{\dot{\vec{q}}^*}=\pdv{L}{\vec{q}^*}-\lambda(t)\vec{f}\]就是Euler-Lagrange equation with constraint。
附註說明一下,這裡的右邊第一項就是我們熟知的作用力,第二項會稱為generalized constraint force。
