Cjue25

Good things take time

新的主題開始，來講軌道。

這節我們講 Bertrand’s Theorem，並且學習用Perturbation Theory的方式來證明，這個證明的技巧在很多問題上都可以應用。

前言

Bertrand’s Theorem：

若粒子受到的吸引力是以下兩種，才能形成封閉橢圓軌道。

  • $\frac{1}{r^2}$
  • SHO (Hooke’s law in 2D or 3D)
Bertrand's Theorem:
If all orbits slightly perturbed from a circular orbit are still closed orbits, then the central attractive force field the particle is moving necessarily are Hookean (i.e. $\vec{F} \propto -\vec{r}$) or Newtonian (i.e. $\vec{F} \propto -\frac{1}{r^2}\hat{r}$).

但要注意兩點：

  • 圓形軌道推你一下看看，不論是什麼方向，都還是能以封閉軌道回來，也就是說即便做了一點點擾動，還是封閉軌道。
  • 這個系統受的力只能一種，不是牛頓就是虎克，不能混在一起。

軌道公式

證明思路：找 EOM $\Rightarrow$ Equation that describes shape $\Rightarrow$ Equation of orbit shape


我們知道軌道公式：

\[m\frac{d^2\vec{r}}{dt^2} = -\frac{\partial V}{\partial \vec{r}}\\ (V=V(r) \text{ 只和 source 的距離有關})\]

在 2D 極座標上，此 orbital plane 在 x-y plane上可以寫成(polar coordinates $(r,\theta)$, with isotropic central force (各方向相同))

\[\left\{ \begin{array}{ll} m\frac{d^2 r}{dt^2}-mr\dot{\theta}^2=-\frac{\partial V}{\partial r}\\ mr^2\dot{\theta} = l \end{array} \right.\\ (l = \text{ angular momentum = constant of the motion})\]
Note: $$ \frac{d\vec{r}}{dt} = \vec{v} = \dot{r}\hat{r} + r\dot{\theta}\hat{\theta} $$ $$ \begin{align} \vec{v}^2&=\dot{r}^2(\hat{r}\cdot\hat{r})+2\dot{r}r\dot{\theta}(\hat{r}\cdot\hat{\theta})+r^2\dot{\theta}^2(\hat{\theta}\cdot\hat{\theta})\\ &=\dot{r}^2+r^2\dot{\theta}^2 \end{align} $$ Lagrangian: $$ L = \frac{m}{2}(\dot{r}^2 + r^2\dot{\theta}^2) - V(r),\quad \frac{d}{dt}\left(\frac{\partial L}{\partial \vec{q}}\right)=\frac{\partial L}{\partial q} $$ $$ \begin{align} r :&\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{r}}\right) = \frac{\partial L}{\partial r},\quad\frac{d}{dt}(m\dot{r})=mr\dot{\theta}^2-\frac{\partial V}{\partial r}\\ \theta :&\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta}}\right) = \frac{\partial L}{\partial \theta},\quad\frac{d}{dt}(mr^2\dot{\theta})=0 \end{align} $$

把$t$換成 $r-\theta$ 的公式，希望剩下 $r(\theta)$ for orbit eq:

第二式

\[\Rightarrow\frac{1}{dt} = \frac{l}{mr^2}\frac{1}{d\theta}\]

代回第一式

\[m\left(\frac{l}{mr^2}\right)^2\frac{d^2r}{d\theta^2} - mr\left(\frac{l}{mr^2}\right)^2 = -\frac{\partial V}{\partial r}\] \[\frac{l^2}{mr^4}\frac{d^2r}{d\theta^2} - \frac{l^2}{mr^3} = -\frac{\partial V}{\partial r}\]

又令

\[u = \frac{1}{r},\quad du = -\frac{1}{r^2}dr\\ dr = -r^2du, \quad \frac{1}{dr}=-\frac{1}{r^2}\frac{1}{du}\]

所以

\[\frac{l^2}{mr^4}\frac{d}{d\theta}\left(-r^2\frac{du}{d\theta}\right) - \frac{l^2}{mr^3} = -\left(\frac{\partial V}{\partial u}\frac{\partial u}{\partial r}\right)=-\left(\frac{\partial V}{\partial u}\times - \frac{1}{r^2}\right)\\ \frac{l^2}{mr^2}\left[\left(\frac{d^2u}{d\theta^2}\right)+\frac{1}{r}\right]=-\frac{1}{r^2}\frac{\partial V}{\partial u}\\ \frac{d^2u}{d\theta^2} + \frac{1}{r} = -\frac{m}{l^2}\frac{\partial V}{\partial u}\]

最後整理得

\[\frac{d^2 u}{d\theta ^2}+u=-\frac{m}{l^2}\frac{\partial V}{\partial u}\equiv J(u)\]

如果 $V(r) (V(u))$ 能得到，那就可以算出 $u(\theta)$ 得到 軌道的形狀。

加入 Perturbation

選擇 Perturbation 變數：能量

在上述的Equation for the orbital shape, 有包含$l$(角動量)，但如果這個值做擾動，被允許改變的話，自由度會太大，不好做。

所以我們採取固定角動量，改對系統的能量做擾動。方法是改變一點速度v，讓它待會是斜斜得跑出去，使得軌道半徑可以是任意的(radius of orbit could be arbitrary)。

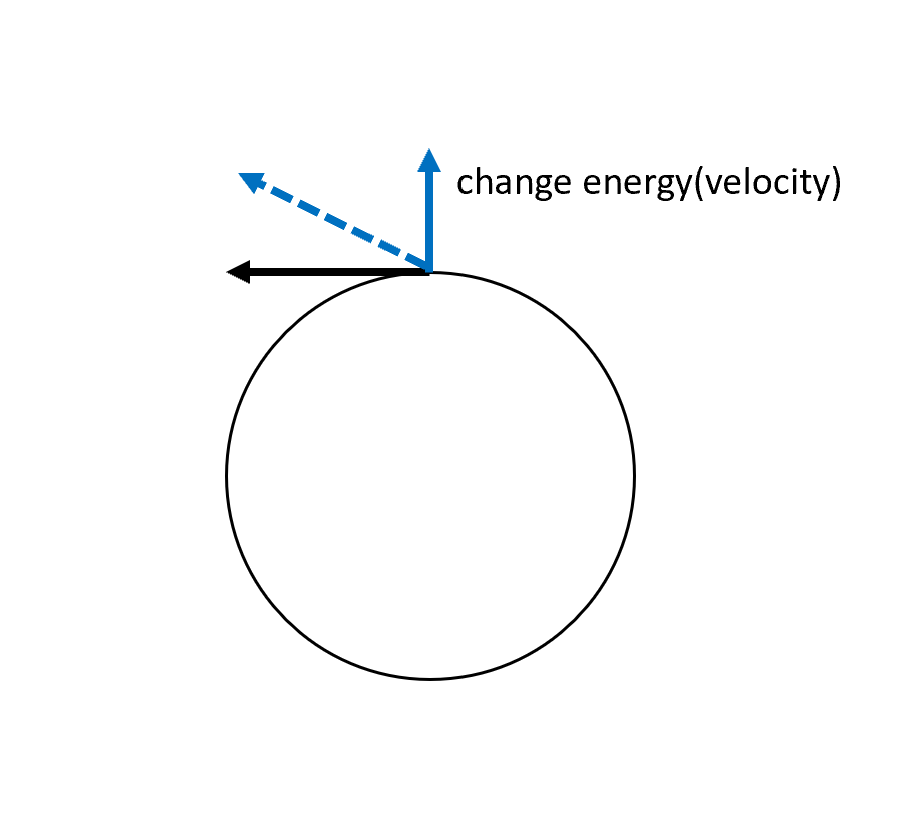
計算 Perturbation 公式：近似到一階

先定非擾動的圓形軌道(“fiducial” circular orbit)

\[u = u_0 = \text{ constant}\]

軌道公式

\[\frac{d^2u_0}{dθ^2} + u_0 = J(u_0)\\ 0 + u_0 = J(u_0)\]

加入對半徑的擾動量

\[u = u_0 + \delta u\]

軌道公式

\[\frac{d^2u}{d\theta^2} + u = J(u) \\ \frac{d^2(u_0 + \delta u)}{d\theta^2} + (u_0 + \delta u) = J(u_0 + \delta u) \\ \frac{d^2u_0}{d\theta^2} + \frac{d^2\delta u}{d\theta^2} + u_0 + \delta u = J(u_0 + \delta u)\\ \frac{d^2\delta u}{d\theta^2} + \delta u + J(u_0) = J(u_0) + J'(u_0)\delta u + \frac{1}{2}J''(u_0)(\delta u)^2 + \cdots\]

近似到一階

\[\frac{d^2\delta u}{d\theta^2} + \delta u = J'(u_0)\delta u\\ \frac{d^2\delta u}{d\theta^2} + (1 - J'(u_0))\delta u = 0\]

討論一階近似結果

$1-J’(u_0)$ 正負

  • $1-J’(u_0) > 0$：$\delta u(\theta)$才會是closed sinusoidal in $\theta$。
  • $1-J’(u_0) < 0$，$\delta u$ 會 exponential 增長，軌跡會變成 spiral out and non-closed。

擾動量的週期性公式

因為 Bertrand’s Theorem 要是封閉軌道，所以我們採用$1-J’(u_0) > 0$，代表$\delta u(\theta)$會以某個特定的$\theta$週期回來。

前面我們定 $u=\frac{1}{r}$，是和中心力場的距離。若是維持圓形$(u=u_0)$，$u$就會不變，但若加上隨著$\theta$做改變的$\delta u$擾動量，代表軌道會有進出(max$\leftrightarrow$min)。

如下圖$\phi$，代表$\theta$週期，可以看到當走過$\phi$的角度後(不用是$2\pi$)，$\delta u$的數值回復到一樣。

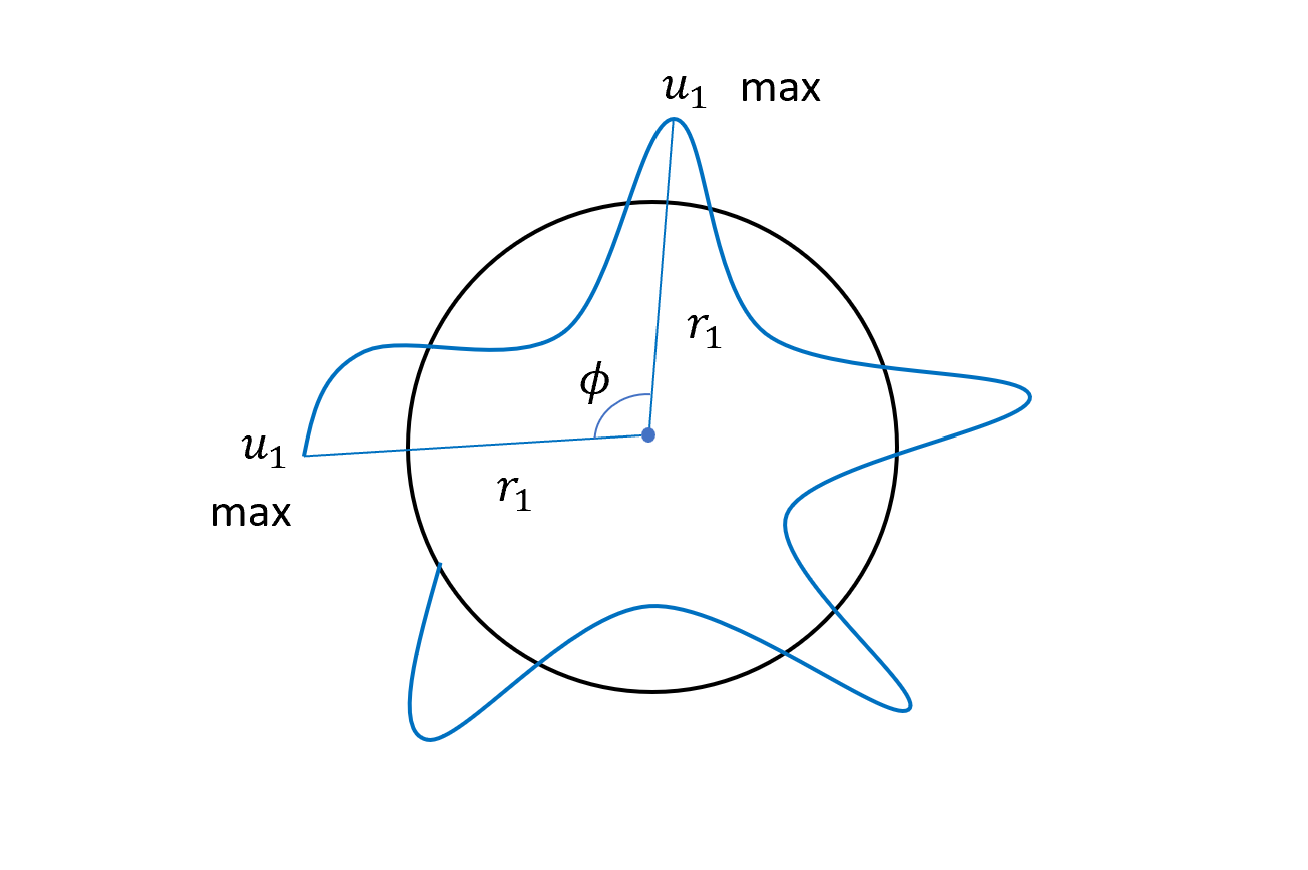
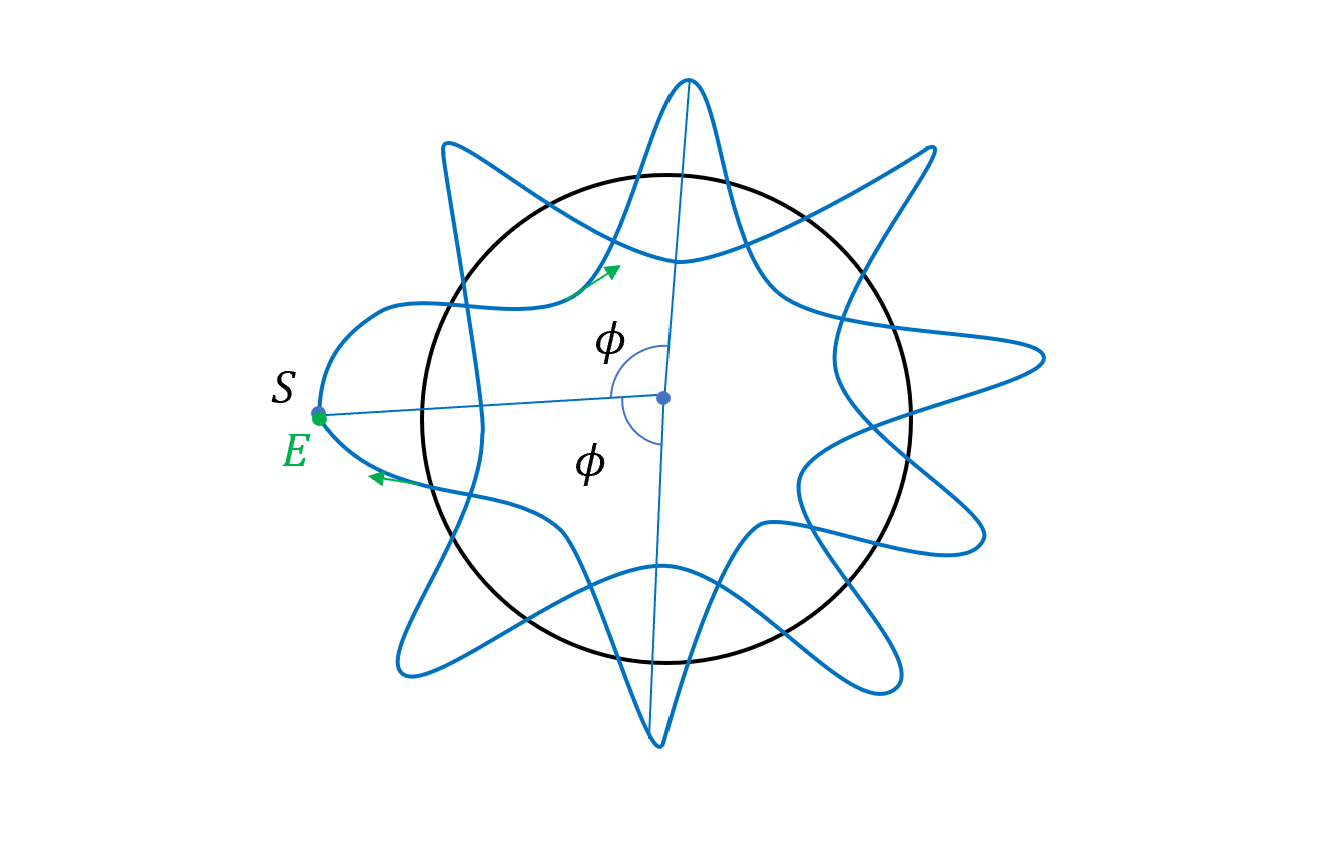
一樣在封閉軌道的前提下，我們可以想像，當這個週期經過很多次後，軌跡可以繞回到原點(“perturbed orbit” repeat)。

這個概念可以用以下公式表示

\[P\cdot\phi=2\pi\cdot q\\ \phi = 2\pi \frac{q}{P} = \text{angular period of } \delta u\]
  • $P$： positive integer，重複$n$次變成一樣 $\delta u$ 的 $\phi$ ($\delta u$ repeats)。
  • $q$：another positive integer。

再代回軌道公式解

\[\delta u = A \cos(\sqrt{1-J'(u_0)} \theta) + B \sin(\sqrt{1-J'(u_0)} \theta)\\ \delta u \text{ period} = \frac{2\pi}{\sqrt{1-J'(u_0)}}\\ \Rightarrow \phi=2\pi \frac{q}{P} = \frac{2\pi}{\sqrt{1-J'(u_0)}}\\ 1-J'(u_0) = \frac{P^2}{q^2} \\ J'(u_0) = 1 - \frac{P^2}{q^2}\]

可以從公式中看到$J’(u)$是非任意的限制項，必須滿足特定的$P,q$，代表受到向心力的限制。(Restrict form, not arbitrary, constraint from of the possible form of the attractive force.)

連續性左右不等價

前面推導出的這個關係式

\[J'(u_0) = 1 - \frac{P^2}{q^2}\]

可以看到

  • LHS(連續)： $u_0$是 tunable (只要是circular + close)，所以 $J’(u_0)$ 會是連續的(continuous function of the energy)。
  • RHS(不連續)： $P, q$ 都是整數，是不連續的。

這樣兩邊要如何等價在一起呢？只能得出結論：$J’(u_0)$ 應該是個常量，不是 $u_0$ 的函式，與 $u_0$ 無關。所以 $u_0$ 怎麼調都不會改變 $J’(u_0)$ 和 $1-\frac{P^2}{q^2}$。


那這樣 $J’(u_0)$ 到底是甚麼？

$J’(u_0)$ 的本質：還要再求高階項

現在我們進一步看$J’(u_0)$，先回顧 unperturbed circular orbit

\[\left\{ \begin{array}{ll} mr\dot{\theta}^2 = \frac{\partial V}{\partial r}\\ mr^2\dot{\theta} = l = \text{fixed in our argument} \end{array} \right.\] \[\begin{align} \dot{\theta} &= \frac{l}{mr^2}\\ mr\left(\frac{l}{mr^2}\right)^2 &= \frac{\partial V}{\partial r} \\ \frac{l^2}{mr^3} &= \frac{\partial V}{\partial r} \\ \frac{1}{l^2} &= \frac{1}{mr^3\frac{\partial V}{\partial r}} \end{align}\]

然後前面有證出三個重要的式子

\[\left\{ \begin{array}{ll} \frac{d^2 u}{d\theta ^2}+u=-\frac{m}{l^2}\frac{\partial V}{\partial u}\equiv J(u)\\ \frac{d^2\delta u}{d\theta^2} + (1 - J'(u_0))\delta u = 0\\ J'(u_0) = 1 - \frac{P^2}{q^2} \end{array} \right.\]

所以

\[\begin{align} J'(u_0) &=1-\frac{P^2}{q^2} \\ &= -\frac{m}{l^2}\frac{\partial^2 V}{\partial u^2}\\ &= -m\frac{\partial^2 V}{\partial u^2}\frac{1}{mr^3\frac{\partial V}{\partial r}}\\ &= -m\frac{\partial^2 V}{\partial u^2}\frac{1}{mr^3(-\frac{1}{r^2})\frac{\partial V}{\partial u}}\\ &= \frac{u\frac{\partial^2 V}{\partial u^2}}{\frac{\partial V}{\partial u}}\Bigg|_{u=u_0} \\ &= u\frac{\partial}{\partial u}\ln\left|\frac{\partial V}{\partial u}\right|\quad\left(\frac{f'(x)}{f(x)} = \ln(f(x))'\right)\\ &= \frac{\partial \ln\left|\frac{\partial V}{\partial u}\right|}{\partial \ln u}\Bigg|_{u=u_0}\quad\left(\frac{\partial \ln u}{\partial u} = \frac{1}{u},\quad u\frac{1}{\partial u} = \frac{1}{\partial \ln u}\right) \end{align}\]

到這裡，$u_0$還是tunable，對應unperturbed circular orbit的不同半徑。

做積分

\[\Rightarrow \ln \frac{\partial V}{\partial u} = (\ln u) \left(1-\frac{P^2}{q^2}\right)\]

得到一個正比的關係

\[\frac{\partial V}{\partial u} \propto u^{1-\frac{P^2}{q^2}}\\ V\propto\int u^\left(1-\frac{P^2}{q^2}\right)\partial u \propto u^\left(2-\frac{P^2}{q^2}\right)\]

至此，代表Force law是被這個Power law限制(跟$J’$有關)，但$P,q$的值還是不確定，需要用到更高階(3rd)的項才能求解。

\[\frac{d^2\delta u}{d\theta^2} + (1- J'(u_0))\delta u = \frac{1}{2}J''(u_0)(\delta u)^2 + \frac{1}{3!}J'''(u_0)(\delta u)^3 +\cdots\]

不過這邊我們先打住，可以看到本節在推導的過程用到SHO的解法，所以下一節也先用SHO來討論高階的情況，之後會再回來繼續解這個問題。

You may also enjoy