(3) 軌道 Bertrand’s Theorem ─ 高階求解得證

前言

第一節

第一節我們提到軌道公式若只近似到一階

\[\frac{d^2\delta u}{d\theta^2} + (1 - J'(u_0))\delta u = 0\]

會得到

\[J'(u_0) = 1 - \frac{P^2}{q^2}\]

可是左側$u_0$可以連續調整，所以應該是連續的函式，但右側$P,q$都是整數，所以是非連續的數值，兩者不對等的情況，代表$J’(u_0)$應該不是$u_0$的函式。

至此$J’(u_0)$只能看到是用來限制Force Law

\[V\propto u^\left(2-\frac{P^2}{q^2}\right)\]

所以若要解軌道問題，只取到一階還不夠，我們必須進一步看更高階的項，才知道$P,q$值該怎麼被確定下來。

\[\frac{d^2\delta u}{d\theta^2} + (1- J'(u_0))\delta u = \frac{1}{2}J''(u_0)(\delta u)^2 + \frac{1}{3!}J'''(u_0)(\delta u)^3 +\cdots\]

第二節

第二節我們先從基本的SHO出發，討論若有高階項的時候，perturbation theory的近似應該要怎麼計算。

這裡也在舉個例子說明為什麼做近似的時候order這麼重要。

熱膨脹係數

我們知道一個金屬尺有一個熱膨脹係數，公式大概是這樣

\[L(\Delta T)=L_0(1+\alpha \Delta T)\\ (\alpha\text{: small, coefficient of thermal expansion})\]

• 先升10度：$L(10\,^{\circ}\mathrm{C})=L_0(1+\alpha\times 10)$
• 再降10度：$L_0(1+\alpha\times 10)(1-\alpha\times 10)=L_0(1-\alpha^2 10 ^2)$

因為$\alpha^2 10 ^2$一定是正數的，那不就代表先升溫再降溫，尺就越變越小了！？

一定哪裡錯了！

回頭看熱膨脹公式的來源

\[L(\Delta T)=L_0+L'(0)\Delta T+\frac{L''}{2}(\Delta T)^2\\ L(\Delta T)\approx L_0(1+\alpha \Delta T)\]

我們最前面得到的公式是做近似到一階而來的$(\alpha = L’(0))$，所以剛剛荒謬的計算是因為取了$\alpha^2$，算到2階了！

因此算物理近似的時候，我們要知道自己一直在哪個order。

Nonlinear Oscillator

一個SHO其實就是一個potential在平衡點附近的近似。

最低階的近似是虎克定律

\[\ddot{x}+x=0\]

如果想要算得更精確，Force Law就要算到高階。在第二節中就討論如果要和週期(頻率)有關

\[\ddot{x}+x=\delta x^3\]

需要近似$\delta$到一階。

\[\ddot{x}+x=\epsilon x^2\]

需要近似$\epsilon$到二階。

現在兩者合併，求這個non-linear oscillator的週期

\[\ddot{x}+x=\epsilon x^2+\delta x^3\]

所以頻率會是$(\epsilon, \delta)$的函式

\[\begin{align} \omega(\epsilon, \delta) &\approx\omega_{00} &&\Rightarrow 1\\ &+\omega_{10}\epsilon &&\Rightarrow\omega_{10}=0\text{ 前面物理和數學的角度都證明過週期要和$\epsilon^2$才有關係}\\ &+\omega_{01}\delta &&\Rightarrow\omega_{01}=-\frac{3}{8}A^2\\ &+2\omega_{11}\epsilon\delta &&\Rightarrow\text{Drop，因為$\epsilon\delta$相對於$\delta$來說是 higher order}\\ &+\omega_{20}\epsilon^2 &&\Rightarrow\omega_{20}=-\frac{5}{12}A^2\\ &+\omega_{02}\delta^2 &&\Rightarrow\text{Drop，因為是 higher order}\\ &+\cdots \end{align}\]

結合在一起

\[\omega(\epsilon, \delta)\approx 1-\frac{3}{8}A^2-\frac{5}{12}A^2\]

• 兩者對振幅$A$都是一樣的order，$\mathcal{O}(A^2)$。
• 之前分開看的修正項，結合之後可以直接相加。

Bertrand 引進高階的意義

回到 Bertrand，我們一樣看到三階

\[\frac{d^2\delta u}{d\theta^2} + (1- J')\delta u = \frac{1}{2}J''(\delta u)^2 + \frac{1}{6}J'''(\delta u)^3\]

令自然頻率為1

\[\frac{d^2\delta u}{d(\sqrt{1-J'}\theta)^2} + \delta u = \frac{J''}{2(1- J')}(\delta u)^2 + \frac{J'''}{6(1- J')}(\delta u)^3\]

類比一下

\[\ddot{x}+x=\epsilon x^2+\delta x^3\]

得到對應的

\[x: \delta u,\quad\epsilon: \frac{J''}{2(1- J')},\quad \delta: \frac{J'''}{6(1- J')}\]

所以可以看到，如果我們一開始只有近似到$J’$一階，等號左右有連續和不連續的不等價，這個不等價代表若我們任意做perturbation，有可能$\omega$不會變。

因為若

\[\frac{d^2\delta u}{d\theta^2} + (1 - J')\delta u = 0\\ \omega=\sqrt{1 - J'}=\sqrt{\frac{P^2}{q^2}}\]

當以為的$J’(u_0)$連續變化時，$\omega$卻因為整數關係所以不一定會變(不連續的)，所以需要引進高階項來平衡$\omega$，使得做任意perturbation，$\omega$維持不變，也符合之前Bertrand’s Theorem說的：即便做了一點擾動，還是要維持是週期性的封閉軌道(orbits slightly perturbed from a circular orbit are still closed orbits)。

求解 $P,q$

補充一下之前Nonlinear Oscillator的例子

\[\ddot{x}+x=\delta x^3\\ \ddot{x}+x=\epsilon x^2\]

我們是說$\epsilon, \delta$很小，但現在對應到$J’$時，我們並沒有說這個值也很小，所以其實本質上問題還有點不太一樣的。

在我們的問題中，很小的值是$\delta u$！

現令$A$是$\delta u$的振幅，可以調得很小

\[\delta u\equiv A\cdot x,\quad x\text{ is dimensionless and order is unity}\\ \frac{d^2\delta u}{d\theta^2} + (1- J'(u_0))\delta u = \frac{1}{2}J''(u_0)(\delta u)^2 + \frac{1}{3!}J'''(u_0)(\delta u)^3 \\ \Rightarrow \ddot{x}+(1-J')x=\frac{J''}{2}A x^2+\frac{J'''}{6}A^2 x^3\]

一樣類比

\[\ddot{x}+x=\epsilon x^2+\delta x^3\]

可以看到order對齊$\mathcal{O}(A^2)$

$\epsilon$：

\[\frac{J''}{2}A\Leftrightarrow(1-J')\epsilon\\ \epsilon=\mathcal{O}(A),\quad\omega\sim\mathcal{O}(\epsilon^2)\]

$\delta$：

\[\frac{J'''}{6}A^2\Leftrightarrow(1-J')\delta\\ \delta=\mathcal{O}(A^2),\quad\omega\sim\mathcal{O}(\delta)\]

整理一下

\[\Rightarrow \frac{d^2 x}{d(\sqrt{1-J'}t)^2} + x = \frac{J''}{2(1- J')}x^2 + \frac{J'''}{6(1- J')}x^3\]

頻率維持不變

若要$\epsilon$和$\delta$這兩項不影響頻率，則

\[\omega(\epsilon, \delta)\approx 1-\frac{3}{8}\delta A^2-\frac{5}{12}A^2\epsilon^2\approx 1\\ \Rightarrow \frac{3}{8}\frac{J''' A^2}{6(1-J')}+\frac{5}{12}\left(\frac{J''A}{2(1-J')}\right)^2=0\]

又

\[J(u) = -\frac{m}{l^2} \frac{\partial V}{\partial u}\\ V(u) \propto u^{2-\frac{P^2}{q^2}}\]

所以

\[\begin{align} J(u) &= -\frac{m}{l^2} \left(2-\frac{P^2}{q^2}\right) u^{\left(1-\frac{P^2}{q^2}\right)} \\ &= -B n u^{n-1},\quad n \equiv 2-\frac{P^2}{q^2} \end{align}\]

代進

\[\frac{3}{8}\frac{J''' A^2}{6(1-J')}+\frac{5}{12}\left(\frac{J''A}{2(1-J')}\right)^2=0\\ \Rightarrow \frac{3}{8} \left(\frac{-B}{6}\right) n(n-1)(n-2)(n-3) u^{n-4} + \frac{5}{12} \frac{(-Bn(n-1)(n-2) u^{n-3})^2}{4(1+Bn(n-1)u^{n-2})} = 0\]

此式若要成立，但$n \neq 0$的話，$n$可以是$1$或$2$。

又或者還可以繼續化簡

\[\Rightarrow -\frac{3}{8} \frac{(n-3)}{6} u^{n-4} + \frac{5}{12} \frac{B}{4} \frac{n(n-1)(n-2) u^{2n-6}}{1+Bn(n-1)u^{n-2}} = 0\\ \Rightarrow -3(n-3) + \frac{5Bn (n-1)(n-2) u^{n-2}}{1+ Bn(n-1) u^{n-2}} = 0\]

然後回來看原本的 unperturbed circular orbit,

\[\begin{align} l^2&=m^2r^2v^2\\ \frac{l^2}{mr^3} &= \frac{\partial V}{\partial r}\\ \frac{l^2}{m} &= r^3 \frac{\partial V}{\partial r} = r \left(-\frac{\partial V}{\partial \frac{1}{r}}\right) = -\frac{1}{u} \frac{\partial V}{\partial u}\\ \because J(u)&=-\frac{m}{l^2} \frac{\partial V}{\partial u} \equiv -B n u^{n-1}\\ \therefore 1 &= -\frac{m}{l^2} \frac{1}{u} \frac{\partial V}{\partial u} = -B n u^{n-1} \frac{1}{u} = -n B u^{n-2}\\ \Rightarrow B &= \frac{-1}{n u^{n-2}} \end{align}\]

得到$B$後代回剛剛算的

\[\begin{align} -3(n-3) &+ \frac{5Bn (n-1)(n-2) u^{n-2}}{1+ Bn(n-1) u^{n-2}}= 0\\ -3(n-3) &+ \frac{(-1)5 n (n-1)(n-2) u^{n-2}\times\frac{1}{nu^{n-2}}}{1+ \frac{-1}{nu^{n-2}}n(n-1) u^{n-2}}= 0\\ -3(n-3) &+ \frac{-5(n-1)(n-2)}{2-n}= 0\\ -3(n-3) &+ 5(n-1)= 0\\ &2n+4=0\\ &n=-2 \end{align}\]

分析$n$的數值，求出$P,q$

綜合以上，若$n\neq 0$的話，

\[n=1, 2, -2\]

配上前面最一開始的定義

\[n = 2 - \frac{P^2}{q^2}\]

分析一下

• $n=1 \Rightarrow 1 = \frac{P^2}{q^2}, \quad P=q=1$
• $n=2 \Rightarrow P=0$, ruled out
• $n=-2 \Rightarrow 4 = \frac{P^2}{q^2},\quad P=2,q=1$

求出了$P,q$的解！

\[(P,q)=(1,1)\text{ or }(2,1)\]

$P,q$對應的軌道圖像

記得前面我們說到這個的Force Law被限制住了

\[V(u) \propto u^{n}=\left(\frac{1}{r}\right)^n\]

現在把$n=1$和$n=-2$代進去得到

\[\left\{ \begin{array}{ll} \frac{1}{r}\quad\Rightarrow\text{ Newtonian Gravity}\\ r^2\quad\Rightarrow\text{ Hooke's Law} \end{array} \right.\]

第一節說$P$代表軌道”up-down”的次數

• Newton：$P=q=1$

\[\theta：0\to 2\pi\\ r\to r_{\text{min}}\to r_{\text{max}}\to r_{\text{min}}\]

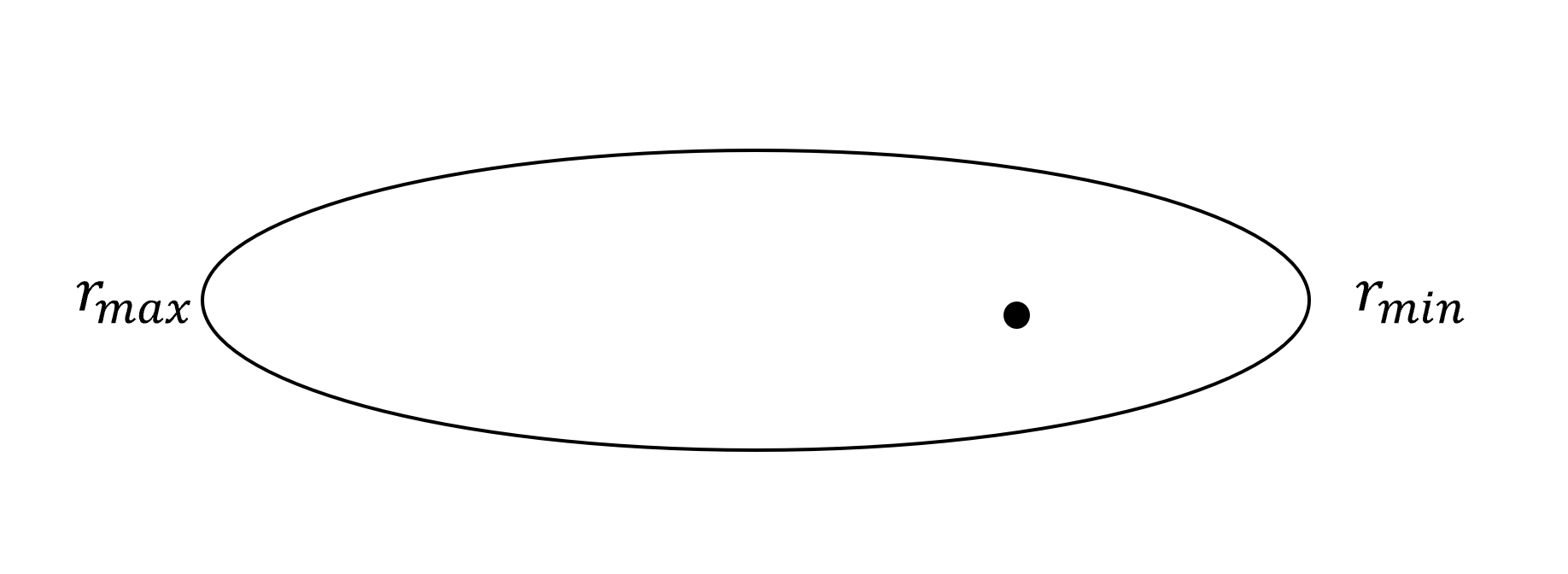
• Hooke’s law：$P=2, q=1$

\[\theta：0\to 2\pi\\ r\to r_{\text{min}}\to r_{\text{max}}\to r_{\text{min}}\to r_{\text{max}}\to r_{\text{min}}\]

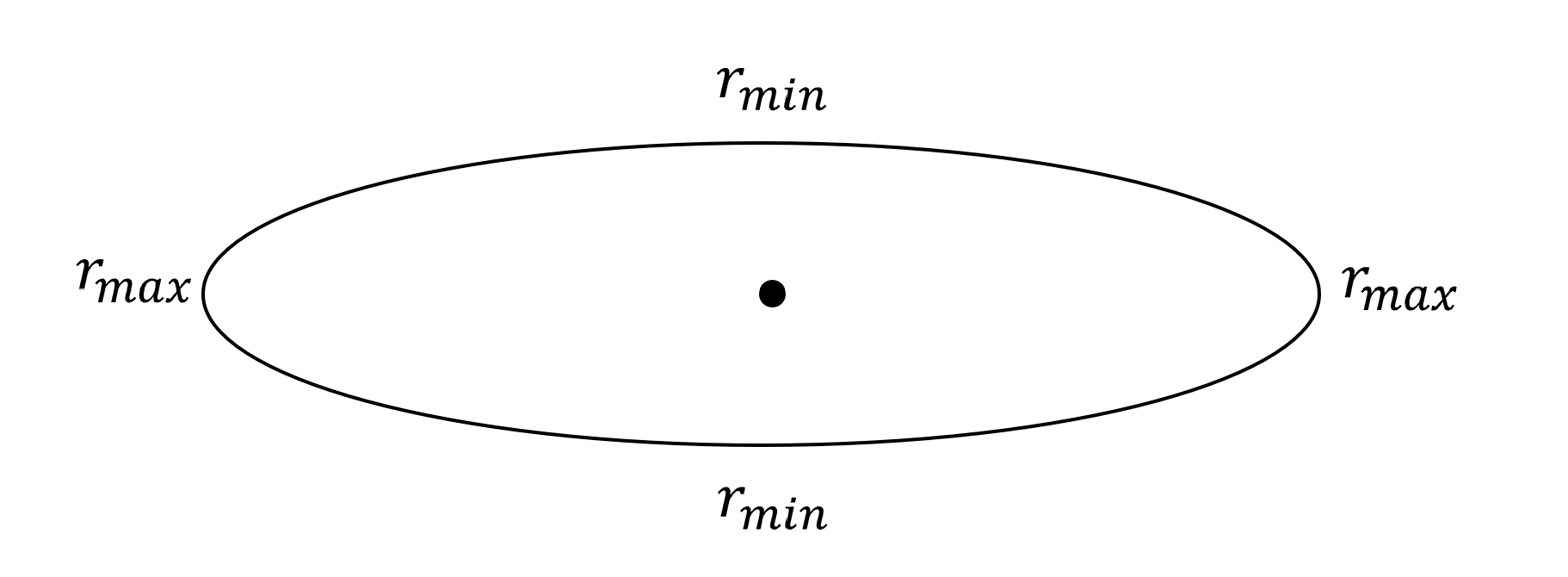
得證Bertrand’s Theorem！