Cjue25

Good things take time

整理一下我們從第五節到第八節在做的事情。

  • 軌道公式位能代 Hooke 可得距離於原點的橢圓軌道。
  • 軌道公式位能代 Newton 重力場可得距離於焦點的橢圓軌道。
  • Hooke 2D 軌道可視為 3D 球面等速直線運動的投影。
  • Newton 求出 Laplace-Runge-Lenze(LRL) vector 守恆量。
  • Hooke 和 Newton 透過 Bohlin Transformation 後，可以看到兩者是同件事情。

畫個圖

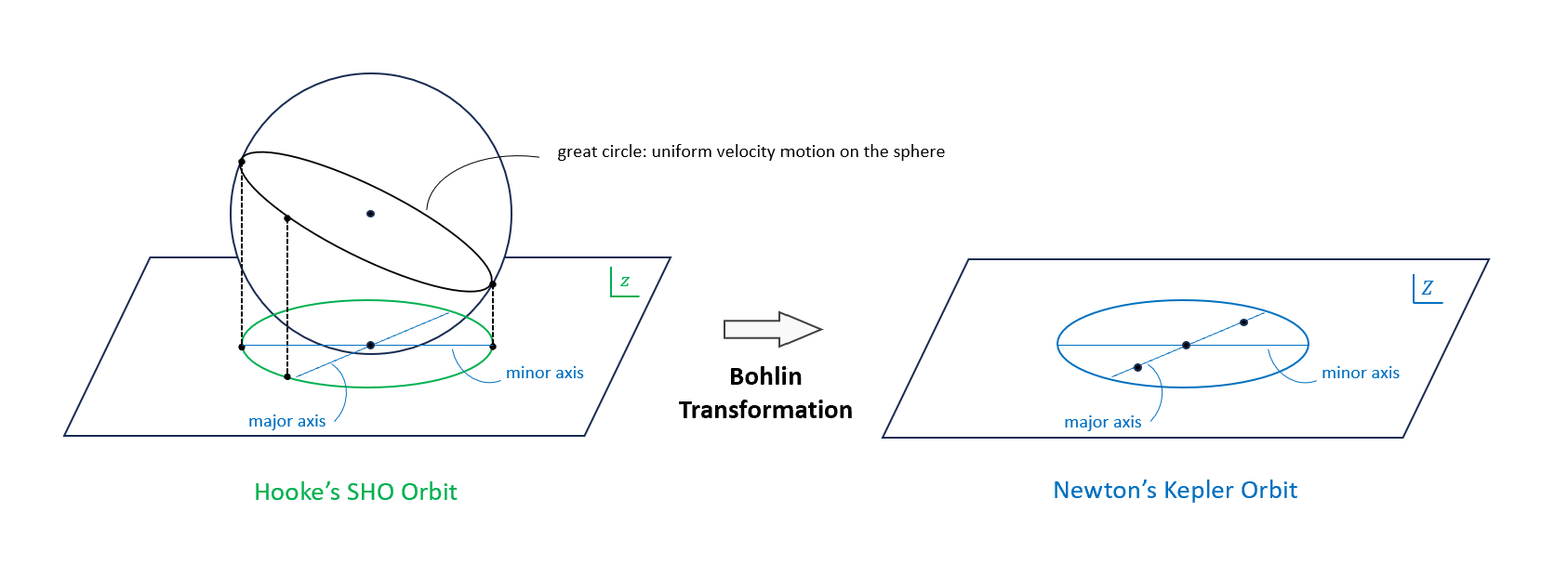
代表 SHO 可以有 Kepler 的物理性質，反之亦然，並且 Kepler 也可以像 SHO 一樣升維到 3D 去看。

兩者彼此分享了各自美好的物理性質，我們來看一下。

離心率、能量、週期


  • 離心率：可以看到離心率的不同，取決於從 3D 球中切的斜面角度，因為長軸就是球的直徑，斜面角度不同覺得了投影的短軸大小，而有不同離心率的橢圓形狀。從這裡可以知道半長軸$a$才是影響其他物理量的主要性質。
  • 能量：SHO 和 Kepler 的能量都只和半長軸$a$有關。
  • 週期：SHO 和 Kepler 的週期都只和半長軸$a$有關，但SHO走一圈，Kepler已經兩倍回來。

克普勒方程與$T(t)$的關係

前一節我們求到 Newton ($T$) 和 Hooke ($t$) Mapping 關係

\[T= \frac{\alpha}{4} (a^2+b^2) \left(2t + \frac{a^2-b^2}{a^2+b^2} \sin 2t\right)\]

定

\[\frac{a^2-b^2}{a^2+b^2} \equiv e'\]

那麼括號中和克普勒方程

\[M=E-e\sin E\]

根本是同一個形式(負號差個$\pi/2$而已)！

$M$也是時間的概念，$E$(Eccentricity Anomaly)是克普勒用幾何形狀做輔助圓時，從圓心算的角度。

這代表什麼？

代表克普勒太強了阿！

他用輔助圓的方式求得位置，相當於是我們現在的倒過來做：從 Kepler 做 transformation 回 SHO，SHO 再升維從 3D 球的大圓看，克普勒方程就是在做這個大圓！

(太神了！)

LRL vector 守恆量的對稱性

從 Noether’s Theorem 知道，有守恆量一定有對應的某個對稱性，那從 Newton 求出的 LRL vector 守恆對應到什麼對稱性呢？

先來看 LRL vector 在 2D SHO 對應的是什麼，這邊不細推過程，直接講答案。

我們知道在SHO

\[\frac{d^2 z}{dt^2}=-z\\ \Rightarrow \frac{d^2z}{dt^2}\frac{dz}{dt}=-z\frac{dz}{dt}\\ \frac{d}{dt}\left(\frac{1}{2}\left(\frac{dz}{dt}\right)^2\right)=-\frac{d}{dt}\left(\frac{z^2}{2}\right)\\ \frac{d}{dt}\left(\frac{1}{2}\left(\frac{dz}{dt}\right)^2+\frac{z^2}{2}\right)=0\]

其中括號中的守恆量(注意也是vector，因為$z$是complex

\[\frac{1}{2}\left(\frac{dz}{dt}\right)^2+\frac{z^2}{2}=\text{constant}\]

用$\mathcal{Z},T$替換後，會得到守恆量正比於LRL vector！

竟然 LRL vector 在 SHO 也有對應的守恆量，那麼一樣可以升維到 3D 球去看，那都是這樣一個正球面了，對稱性很明顯了。

結語

不論是Bertrand’s Theorem還是Bohlin Transformation，牛頓虎克都有很多共同點，從Kepler和SHO的軌道角度來看，算是一家親了吧XD

You may also enjoy