量子 ─ Variational Principle 估算 Ground State Energy
對於一個系統的 Hamiltonian $H$,在不解 time-independent SE 的情況下,我們可以利用 variational principle 算出 ground state energy $E_{gs}$ 的 upper bound 。
Upper Bound for Ground State Energy
\[E_{gs} \leq \left\langle \psi\vert H \vert\psi\right\rangle\equiv\left\langle H \right\rangle\]其中 $\psi$ 為 normalized function。
這個公式理解的意思就是,假設一個任意的$\psi$,算出來的$H$期望值一定會大過基態能量。
想法其實也很直接,因為如果選到的$\psi$是激發態的,那算出來的$\langle H \rangle$ 一定會超過$E_{gs}$。
每一次測量得到的能量可能有高有低,但最低不會低過基態,整體而言平均(期望值)當然就一定超過基態。
(證明:Griffiths 8.1,記得H的期望值就是能量。)
例子一:1D harmonic oscillator
\[H=-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+\frac{1}{2}m\omega^2x^2\]我們以前解過Exact的解$E_{gs}=\frac{1}{2}\hbar\omega$。
現在挑個高斯波函數
\[\psi(x)=Ae^{-bx^2}\]用normalization求係數A,然後算(第二行就是在算泛函的極值,所以才說是變分吧)
\[\langle H \rangle=\langle T \rangle+\langle V \rangle=\frac{\hbar^2 b}{2m}+\frac{m\omega^2}{8b}\\ \frac{d}{db}\langle H \rangle=0\Rightarrow b=\frac{m\omega}{2\hbar}\]得
\[\langle H \rangle_{min}=\frac{1}{2}\hbar\omega\]正是我們原本的Exact的解了!當然這也是因為我們一開始挑的波函數就是正解,但相較之下用變分真的很快!
例子二:delta function potential
\[H=-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}-\alpha\delta(x)\]一樣以前解過Exact的解$E_{gs}=-\frac{m\alpha^2}{2\hbar^2}$。
挑個高斯波函數
\[\psi(x)=Ae^{-bx^2}\] \[\langle H \rangle=\frac{\hbar^2 b}{2m}-\alpha\sqrt{\frac{2b}{\pi}}\\ \frac{d}{db}\langle H \rangle=0\Rightarrow b=\frac{2m^2\alpha^2}{\pi\hbar^4}\]得
\[\langle H \rangle_{min}=-\frac{m\alpha^2}{\pi\hbar^2}\]因為$\pi>2$,所以比我們的正解還要高一點。
例子三:不連續的波函數 for infinite sqare well
雖然前面說可以挑任意的normalized wave function,但如果是$\psi$是不連續的,在算$\langle T \rangle$碰到二次微分,但依然可以解。
\[H=-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}\]一樣以前解過Exact的解$E_{gs}=-\frac{\pi^2\hbar^2}{2ma^2}$。
挑個三角波函數
\[\psi(x)= \begin{cases} Ax,\quad\quad 0\leq x \leq \frac{a}{2}\\ A(a-x),\quad\frac{a}{2}\leq x \leq a\\ 0,\quad\quad\text{otherwise} \end{cases}\]一階微分變成step function
\[\frac{d\psi(x)}{dx}= \begin{cases} A,\quad\quad 0\leq x \leq \frac{a}{2}\\ -A,\quad\quad\frac{a}{2}\leq x \leq a\\ 0,\quad\quad\text{otherwise} \end{cases}\]二階微分就會變成delta function,所以可得
\[\langle H \rangle=\frac{12\hbar^2}{2ma^2}\]一樣大過正解。
意義
雖然這真的很方便,但是為什麼會需要算這個呢?
這個通常都應用在複雜的分子計算,選個有多參數的wave funcion,算$\langle H \rangle$,求參數得最小的$\langle H \rangle$來估基態能量,大部分的時候都滿接近的。
不過因為只是upper bound,所以其實我們也不知道會有多接近真實的基態能量就是了。
接下來,我們就來試試看怎麼用這個方法來算幾個簡單的分子模型!
原子分子模型
Helium - 2個質子2個電子
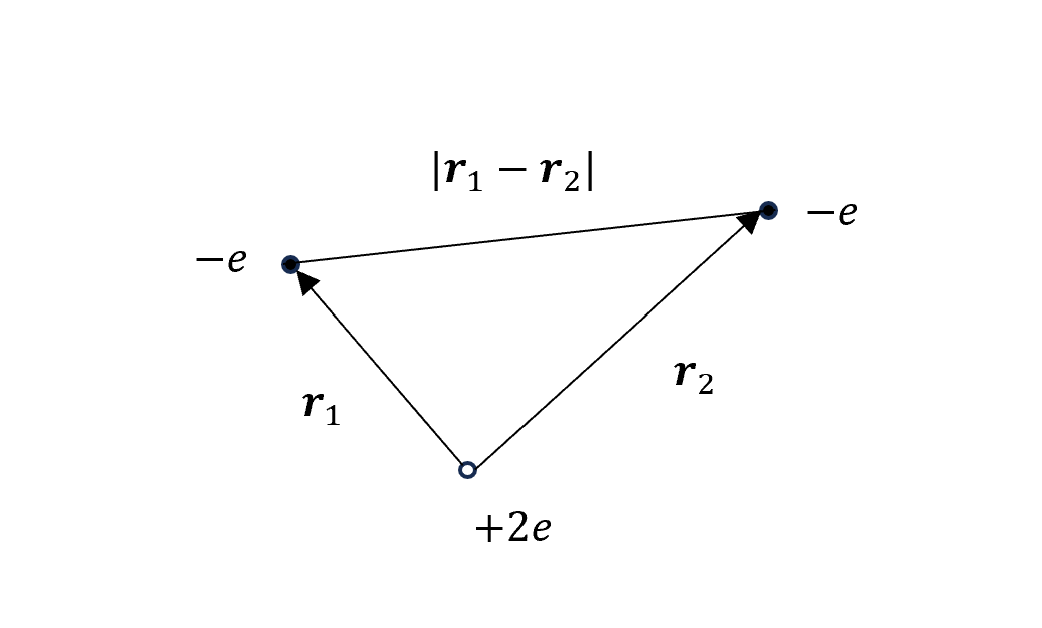
兩個電子繞著核子(兩個質子),列出 Hamiltonian,位能的部分包含各自對質子的吸引力和彼此的排斥力
\[H = -\frac{\hbar^2}{2m}(\nabla_1^2 + \nabla_2^2) - \frac{e^2}{4\pi \epsilon_0} \left(\frac{2}{r_1} + \frac{2}{r_2} - \frac{1}{|\mathbf{r_1} - \mathbf{r_2}|}\right)\]我們先不管最後一項電子排斥力,那就是算類似兩個獨立的氫原子,只是質子是2e,所以直接可以乘
\[\psi_0(\mathbf{r_1}, \mathbf{r_2}) \equiv \psi_{100}(\mathbf{r_1})\psi_{100}(\mathbf{r_2}) = \frac{8}{\pi a^3} e^{-2(r_1+r_2)/a}\]把這個 $\psi_0$當作我們要算 $E_{gs}$ 的假設 (trial wave function)
\[H\psi_0=(8E_1+V_{ee})\psi_0\\ \langle H \rangle=8E_1+\langle V_{ee} \rangle\]這時候我們再去算電子間的排斥力 $\langle V_{ee} \rangle$
\[\langle V_{ee} \rangle = \left(\frac{e^2}{4\pi \epsilon_0}\right) \left(\frac{8}{\pi a^3}\right)^2 \int \frac{e^{-4(r_1+r_2)/a}}{|\mathbf{r_1} - \mathbf{r_2}|} d^3 \mathbf{r_1} d^3 \mathbf{r_2}\\ = \frac{5}{4a} \left( \frac{e^2}{4\pi \epsilon_0} \right) = \frac{5}{2} E_1 = 34 \text{ eV}\]總和就是
\[\langle H \rangle= -109\text{eV} + 34\text{eV}= -75\text{eV}\]非常接近實驗值-78.975eV了!
初始假設考慮電子之間的作用力
但還不夠好,主要原因是我們一開始假設的 $\psi_0$ 是建立在不管電子之間的作用力,所以現在我們重新考慮。
我們可以想像一個電子和兩個質子整合在一起,然後另外一顆電子視這個雲(effective nuclear)的charge為Z(所以會小於2),這樣trial wave function
\[\psi_1(\mathbf{r_1}, \mathbf{r_2}) \equiv \frac{Z^3}{\pi a^3} e^{-Z(r_1+r_2)/a}\]然後重新寫 Helium 的 Hamiltonian
\[H = -\frac{\hbar^2}{2m}(\nabla_1^2 + \nabla_2^2) - \frac{e^2}{4\pi\epsilon_0} \left(\frac{Z}{r_1} + \frac{Z}{r_2}\right) + \frac{e^2}{4\pi\epsilon_0} \left(\frac{(Z-2)}{r_1} + \frac{(Z-2)}{r_2} + \frac{1}{|\mathbf{r_1} - \mathbf{r_2}|}\right)\]得到
\[\langle H \rangle = 2Z^2E_1 + 2(Z-2)\left(\frac{e^2}{4\pi\epsilon_0}\right)\left\langle\frac{1}{r}\right\rangle + \langle V_{ee}\rangle\\ \langle V_{ee} \rangle = \frac{5Z}{8a} \left( \frac{e^2}{4\pi\epsilon_0} \right) = -\frac{5Z}{4} E_1\\ \langle H \rangle = [-2Z^2 + (27/4)Z]E_1\]
這時我們的Z就是一個variational parameter,可以用來最小化 $\langle H \rangle$,馬上來取極值
就又更接近我們的實驗值-78.975eV囉!
Hydrogen Molecule Ion - 2個質子1個電子
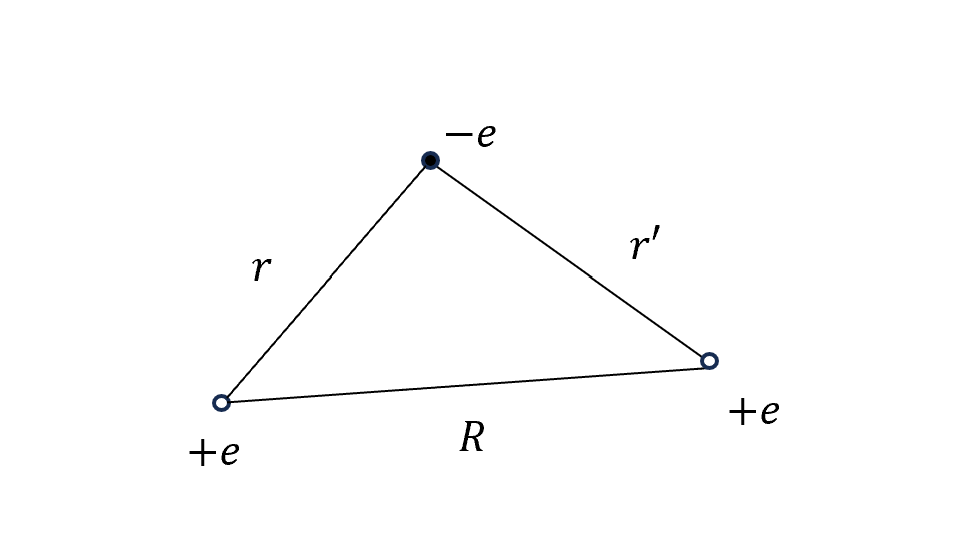
接下來看 $H_2^+$,先假設兩個質子是固定的,那麼 Hamiltonian
\[H = -\frac{\hbar^2}{2m}\nabla^2 - \frac{e^2}{4\pi\epsilon_0}\left(\frac{1}{r} + \frac{1}{r'}\right)\]我們現在一樣要來找 $E_{gs}$,不過這次還有一個重點是,這個groud state energy也代表了這個系統是否是”bonds”,來看最後得到的能量是不是小於一個氫原子+額外的自由質子(-13.6eV)。
這次挑選的 trial wave function,用氫原子的groud state,然後電子分別對這兩顆質子都有關聯,得最後的 trial wave function
\[\psi_0(\mathbf{r}) = \frac{1}{\sqrt{\pi a^3}}e^{-r/a}\\ \psi=A[\psi_0(r)+\psi_0(r')]\]稱這樣的作法為 LCAO (molecular wave function as a linear combination of atomic orbits)
算 Hamiltonian
\[H\psi = A\left[-\frac{\hbar^2}{2m}\nabla^2 - \frac{e^2}{4\pi\epsilon_0}\left(\frac{1}{r} + \frac{1}{r'}\right)\right][\psi_0(r) + \psi_0(r')]\\ = E_1\psi - A\left(\frac{e^2}{4\pi\epsilon_0}\right)\left[\frac{1}{r'}\psi_0(r) + \frac{1}{r}\psi_0(r')\right]\\ \langle H\rangle = E_1 - 2|A|^2\left(\frac{e^2}{4\pi\epsilon_0}\right)\left[\langle\psi_0(r)|\frac{1}{r'}|\psi_0(r)\rangle + \langle\psi_0(r)|\frac{1}{r}|\psi_0(r')\rangle\right]\]再算兩個質子之間的排斥力
\[V_{pp} = \frac{e^2}{4\pi\epsilon_0}\frac{1}{R} = -\frac{2a}{R}E_1\]合併($F(x)$ unit 為 $-E_1$)
\[F(x) = -1 + \frac{2}{x}\left\{\frac{(1-(2/3)x^2)e^{-x} + (1+x)e^{-2x}}{1+(1+x+(1/3)x^2)e^{-x}}\right\}\\ x\equiv \frac{R}{a}\]畫出圖
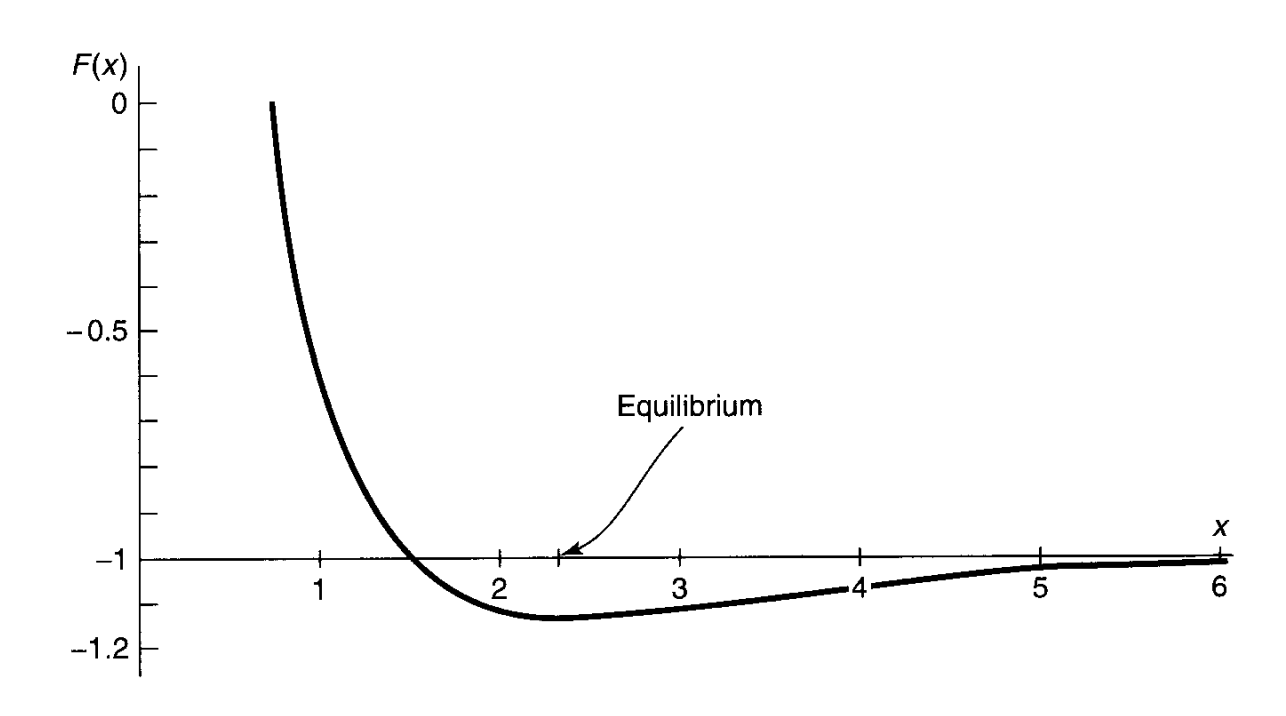
$F(x)$ = -1 的位置就是氫原子的 ground state(-13.6 eV),所以圖中箭頭指出的確bonding是會發生的(小於完全解離後的氫原子+自由質子)!
這就稱為共價鍵covalent bond,也對應我們最前面 LCAO 的假設,一顆電子被兩個質子share。
再進一步看結合能,算要完全解離成氫原子+自由質子所需的能量,所以$x$用2.5代入,得到$F(x)\approx -1.1296$,和氫原子基態差($0.1296\times13.6=1.8$ eV)就是結合能,與實驗~2.8eV也算相近了,當然如果能選更好的trial wave function,$H_2^+$的$E_{gs}$就會越低,鍵結越強,結合能就能越到越接近準確的實驗數值囉!
Hydrogen Molecule - 2個質子2個電子
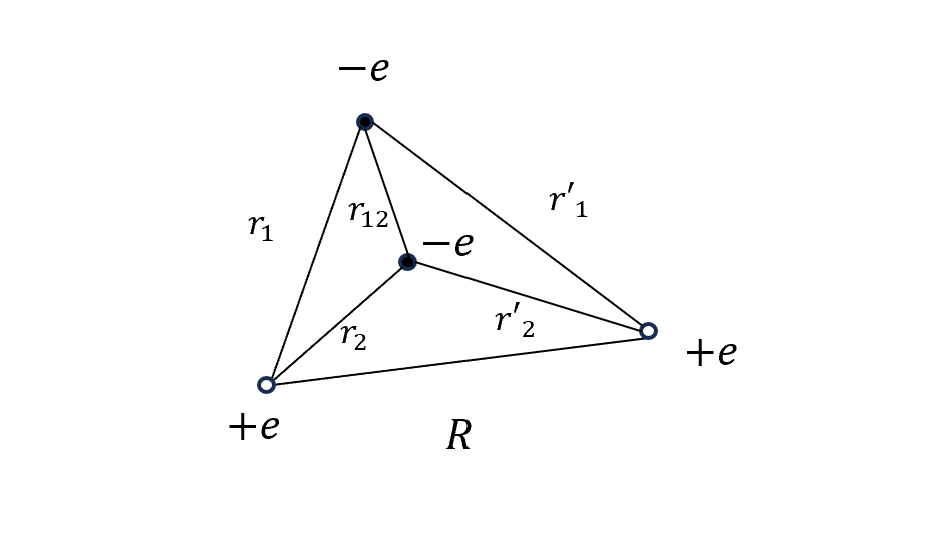
最後一個例子,氫分子~
在 Hydrogen Molecule Ion 的基礎上再多放一顆電子,Hamiltonian 包含兩個電子之間的排斥力、兩個質子間的排斥力還有每個電子對每個質子的吸引力
\[H\psi = -\frac{\hbar^2}{2m}\nabla^2 + \frac{e^2}{4\pi\epsilon_0}\left(\frac{1}{r_{12}}+\frac{1}{R} - \frac{1}{r_1}-\frac{1}{r'_1}- \frac{1}{r_2}-\frac{1}{r'_2}\right)\]一樣來找 trial wave function,可以寫成兩種形式 Heitler-London approximation
\[\psi_{\pm}(\mathbf{r}_1, \mathbf{r}_2)=A_{\pm}[\psi_0(r_1)\psi_0(r'_2)\pm\psi_0(r'_1)\psi_0(r_2)]\]- $+$:symmetric spatial wave function, antisymmetric(singlet) electron spin state
- $-$:antisymmetric spatial wave function, symmetric(triplet) electron spin state
Addition of Angular Momenta of 2 particles:
如果選擇的兩個粒子 spin = 1/2,spin up/down結合共有四種方式。
兩個全同粒子的波函數:
$$ \psi_{\pm}(\mathbf{r}_1, \mathbf{r}_2)=A[\psi_a(\mathbf{r}_1)\psi_b(\mathbf{r}_2)\pm\psi_b(\mathbf{r}_1)\psi_b(\mathbf{r}_2)] $$
(從這條也可以知道,電子不能有same state($\psi_a\neq\psi_b$),不然anti完,就沒有wave function了。)
再進一步結合spin $$ \psi(\mathbf{r}_1,\mathbf{r}_2)\chi(1,2) $$ 如果是電子的話,因為是antisymmetric,所以 $$ \psi(\mathbf{r}_1,\mathbf{r}_2)\chi(1,2) = -\psi(\mathbf{r}_2,\mathbf{r}_1)\chi(2,1) $$ 得
因為也不知道哪個會是主要的形式,所以就一起計算。
動能
\[\left\langle-\frac{\hbar^2}{2m}\nabla^2_1\right\rangle=E_1+\left(\frac{e^2}{4\pi\epsilon a}\right)\frac{1\pm IX}{1\pm I^2}\]有兩個電子,所以之後要乘兩倍。
位能:電子 - 質子
\[\left\langle-\frac{e^2}{4\pi\epsilon r_1}\right\rangle=-\frac{1}{2}\left(\frac{e^2}{4\pi\epsilon a}\right)\frac{1+D\pm 2IX}{1 \pm I^2}\]有四組,乘四倍。
位能:電子 - 電子
\[\langle V_{ee} \rangle = \left(\frac{e^2}{4\pi\epsilon a}\right)\frac{D_2\pm X_2}{1\pm I^2}\]位能:質子 - 質子
\[\frac{e^2}{4\pi\epsilon R}\]全部結合
\[\langle H \rangle _{\pm}=2E_1\left[1-\frac{a}{R}+\frac{2D-D_2\pm(2IX-X_2)}{1\pm I^2}\right]\]- $\langle H \rangle_+$:2 electrons in the singlet spin configuration
- $\langle H \rangle_-$:2 electrons in the triplet spin configuration
畫出圖
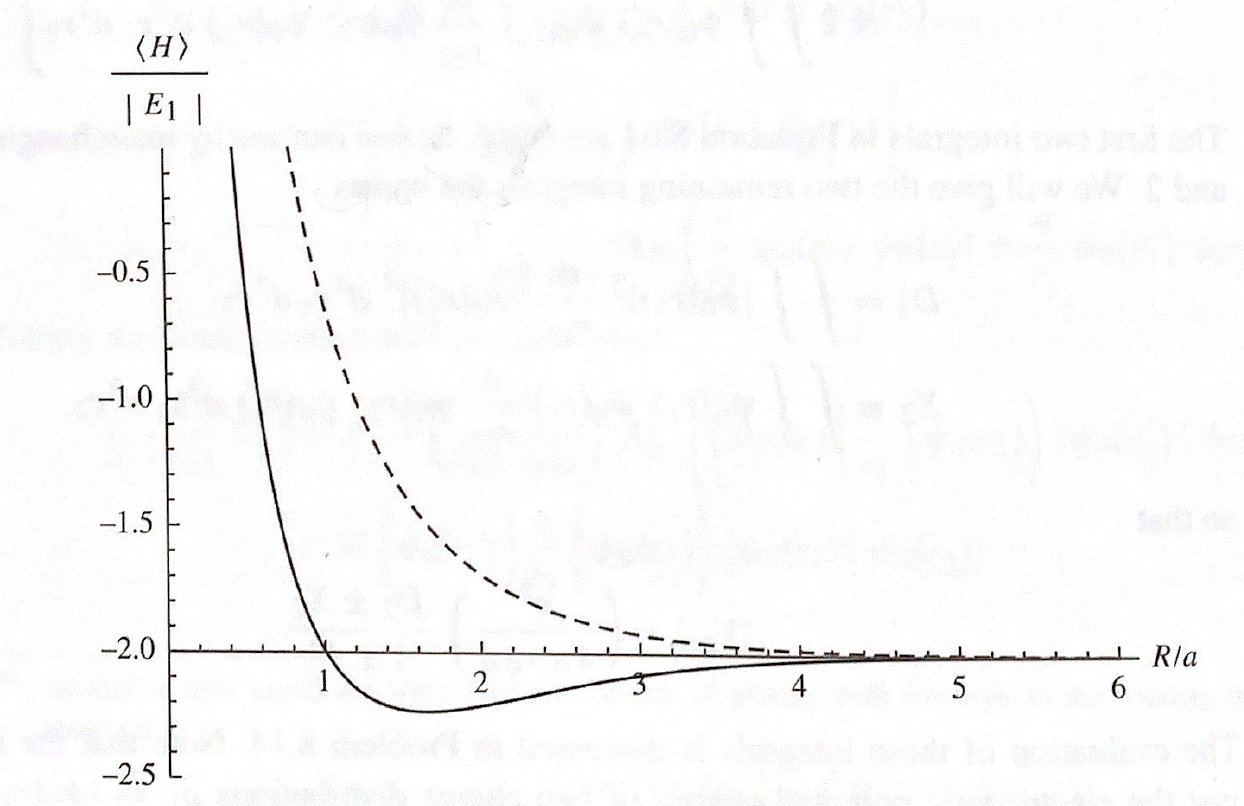
(solid curve: $\langle H \rangle_+$, dashed curve: $\langle H \rangle_-$)
可以看到$\langle H \rangle_+$有bond state,binding energy約為 3.15 eV(實驗值為 4.75 eV)!
Exchange Splitting
我們把兩者的差別稱為 exchange splitting $J$
\[J= \langle H \rangle_+ - \langle H \rangle_- = 4E_1\frac{(D_2-2D)I^2-(X_2-2IX)}{1-I^4}\]對於氫分子來說,算出來約 -10 eV,singlet 能量較低,也代表會比較傾向電子反排列(spin anti-aligned)。
Spin-Spin Interaction
如果要考慮電子之間的(磁性的)spin-spin interaction,像是我們之前在算 hyperfine splitting 一樣,數值大概是 $10^{-4}$ eV,數量級太小了所以可以忽略。
Feromagnetism vs anti-Ferromagnetism from Electrostatics
所以在不考慮 spin-spin interaction 的情況下,exchange splitting 可以給我們重要的一個意義:
Not a magnetic interaction accounts for ferromanetism, but an electrostatic one!
以氫分子來說,我們前面在算的都是電子間的排斥力,或是和質子間的吸引力,計算的Hamiltonian其實都沒有實際算spin。而光靠這點,就可以看出電子傾向的反向排列方式,算是一種反磁性了(a sort of inchoate anti-ferromagnet)!
很神奇吧!
