(5) 軌道 Hooke ─ SHO 橢圓軌道形狀

從第一節可知，描述軌道形狀的軌道公式

\[\frac{d^2u}{d\theta^2} + u = J(u), \quad J(u) = -\frac{m}{l^2}\frac{dV}{du}, \quad u \equiv \frac{1}{r}\]

接下來我們位能代 Hooke’s Law (SHO) 算算看。

SHO 位能代入軌道方程

SHO 位能 (2-D isotropic)

\[V(u) \equiv \frac{m\omega^2}{2}r^2 \equiv \frac{m\omega^2}{2}\frac{1}{u^2},\quad \omega: \text{natural frequency}\]

拆解一下

\[\Rightarrow \frac{d^2u}{d\theta^2} = -u - \frac{m}{l^2}\frac{dV}{du} = -\frac{\partial}{\partial u}\left(\frac{u^2}{2} + \frac{m}{l^2}V(u)\right) \quad -(1)\]

這行如果把 $\theta$ 看成時間，$u$ 看成位移，那對應的就是

\[\frac{d^2u}{d\theta^2} \Rightarrow \frac{d^2x}{dt}\\ -\frac{\partial \cdots}{\partial u} \Rightarrow -\frac{\partial \cdots}{\partial x}\]

那(1)式就可以視為

\[a = \frac{F}{m} = -\frac{\partial \text{(potential energy)}}{m\partial x}\\ \left(\frac{d^2x}{dt} = -\frac{\partial \cdots}{m \partial x},\quad\frac{d^2u}{d\theta^2}=-\frac{\partial V}{M\partial u}\quad M=1\right)\]

不過是二階方程，比較難解，我們改用別的方式降階來解。

用能量守恆計算

能量守恆公式 (analogy to the conservation of mechanical energy)

\[\frac{1}{2}\left(\frac{du}{d\theta}\right)^2 + \left(\frac{u^2}{2} + \frac{m}{l^2}V(u)\right) = \text{constant} \equiv c \quad -(2)\]

(對比一下可以看到，從能量守恆的角度出發比較好解，因為(1)式是2階,(2)式是1階，可以降階處理。)

開始計算

\[\begin{align} \frac{1}{2}\left(\frac{du}{d\theta}\right)^2 + \left(\frac{u^2}{2} + \frac{m}{l^2}\frac{m\omega^2}{2}\frac{1}{u^2}\right) &= c\\ \left(u\frac{du}{d\theta}\right)^2 + u^4 + \frac{m^2\omega^2}{l^2} &= 2cu^2\\ \frac{1}{4}\left(\frac{d(u^2)}{d\theta}\right)^2 + (u^2)^2 + \frac{m^2\omega^2}{l^2} &= 2c(u^2)\\ \left(\frac{d(u^2)}{d(2\theta)}\right)^2 + (u^2)^2 + \frac{m^2\omega^2}{l^2} &= 2c(u^2)\\ \end{align}\] \[\left(\because\frac{du^2}{d2\theta}\frac{d2\theta}{d\theta} = \frac{du^2}{d\theta} = \frac{du^2}{d2\theta} \times 2,\quad\therefore\frac{1}{2}\frac{du^2}{d\theta}=\frac{du^2}{d2\theta}\right)\]

\[\begin{align} \Rightarrow \left(\frac{du^2}{d2\theta}\right) &= \pm \sqrt{2c\cdot u^2 - (u^2)^2 - \frac{m^2\omega^2}{l^2}}\\ &= \pm \sqrt{-(u^2-c)^2 + \left(c^2 - \frac{m^2\omega^2}{l^2}\right)}\\ \Rightarrow \left(\frac{d(u^2-c)}{d2\theta}\right) &= \pm \sqrt{-(u^2-c)^2+\left(c^2-\frac{m^2\omega^2}{l^2}\right)}\quad -(3) \end{align}\]

這裡等號左側多加一個$-c$沒差，反正是常數。

現令

\[\frac{u^2-c}{\sqrt{c^2-\frac{m^2\omega^2}{l^2}}} = \xi\]

(3)式會變成(if we have suitably chosen the origin of $\theta$)

\[\begin{align} \Rightarrow \frac{d\xi}{d(2\theta)} &= \pm\sqrt{-\xi^2+1},\quad \xi = \cos2\theta\\ \Rightarrow u^2 &= \sqrt{c^2-\frac{m^2\omega^2}{l^2}} \cos2\theta + c\\ &= \frac{1 + \sqrt{1-\frac{m^2\omega^2}{l^2c^2}} \cos(2\theta)}{\frac{1}{c}} \end{align}\]

最後得軌道形狀

\[r^2 = \frac{1/c}{1+\epsilon \cos 2\theta}\\ \epsilon = \sqrt{1-\frac{m^2\omega^2}{l^2c^2}}\]

但看起來有點怪，

• 因為現在算的$r$是取自原點，而且參數是$r^2, 2\theta$。
• 以前算的橢圓軌道 $r = \frac{A}{1+e\cos\theta}$ 是起自焦點，參數是$r, \theta$。

但還沒完，再繼續算！

化為熟悉的橢圓形式

前面算到

\[r^2 = \frac{1/c}{1+\epsilon \cos 2\theta}\]

我們簡化一下

\[\Rightarrow r^2 + r^2 \epsilon (\cos^2\theta - \sin^2\theta) = \frac{1}{c}\\ (\because\cos 2\theta = \cos^2 \theta - \sin^2 \theta)\] \[r^2 (1+\epsilon) \cos^2\theta + r^2 (1-\epsilon) \sin^2\theta = \frac{1}{c}\\ (\because r^2 = r^2 (\cos^2\theta + \sin^2\theta)\]

因為SHO是從原點開始算的，所以在極座標我們可以表示

\[r\cos\theta \equiv x,\quad r\sin\theta \equiv y\]

代進去

\[\Rightarrow (1+\epsilon)x^2 + (1-\epsilon)y^2 = \frac{1}{c}\]

同除

\[\frac{x^2}{\left(\sqrt{\frac{1}{c(1+\epsilon)}}\right)^2} + \frac{y^2}{\left(\sqrt{\frac{1}{c(1-\epsilon)}}\right)^2} = 1\]

可以看到這個式子依然是橢圓！(Standard form of an ellipse in rectangular coordinates)

不過原點是在中間。

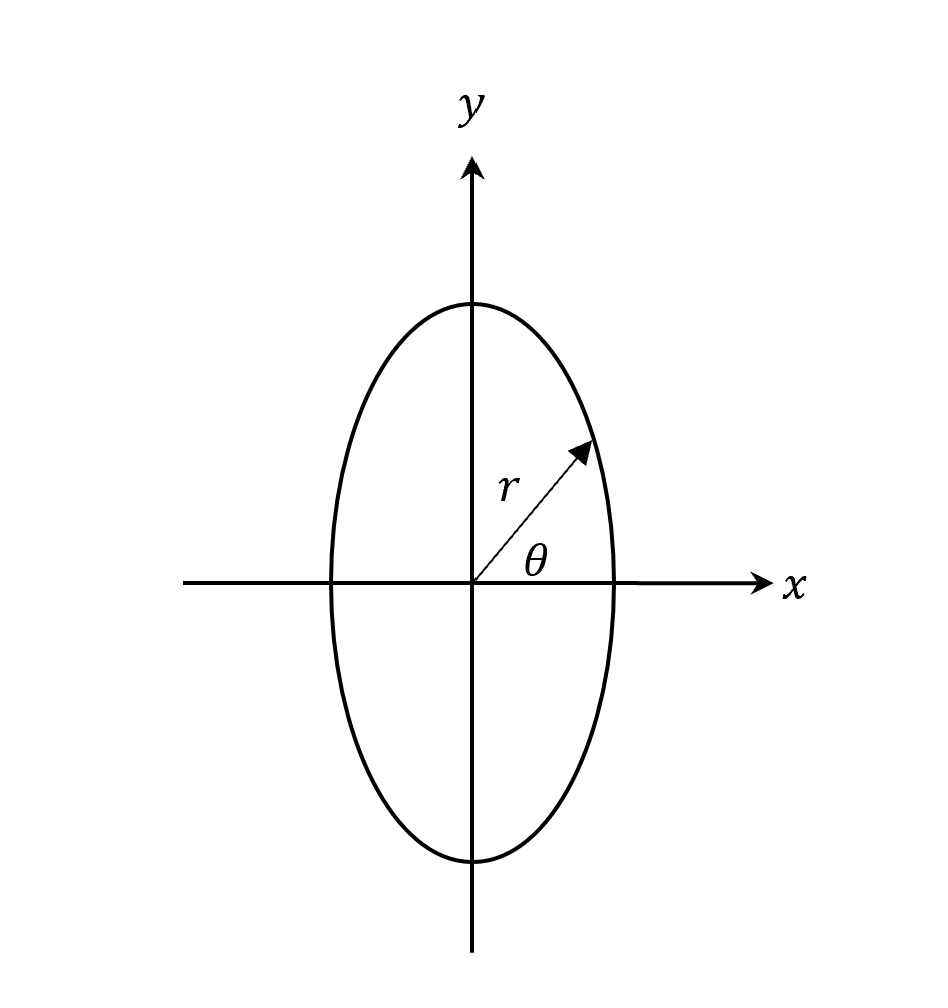
對比 Gravitational Field

對比從牛頓重力場導出來的(下一節推導)

\[r = \frac{A}{1+e\cos\theta}\]

現在從SHO，其實也可以轉換一下

\[r^2 = \frac{1/c}{1+\epsilon\cos2\theta} \Rightarrow R = \frac{1/c}{1+\epsilon\cos\Theta}\]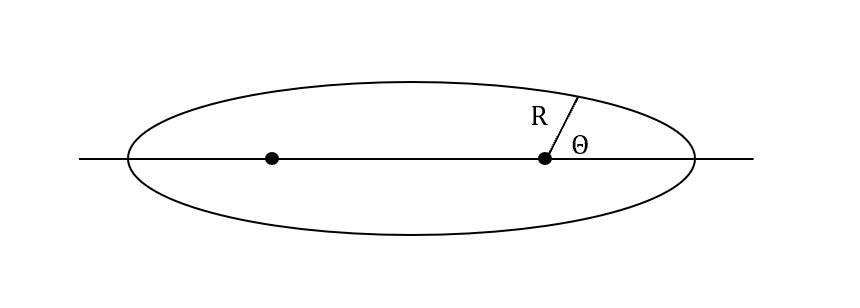

SHO仍然可以”視為”某種橢圓軌道，所以至此可以稍微有點感覺，不管橢圓軌道是哪種方法求出來的，這兩個方法其實都會是同一件事情！