(1) 相對 ─ 伽利略轉換 Galilean Transformation
新的主題開始,來講相對論。
要講相對論,大家很熟悉的數學一定是勞倫茲轉換。
但在這之前,我們先複習一下傳統力學的伽利略轉換。
慣性座標系及慣性觀察者
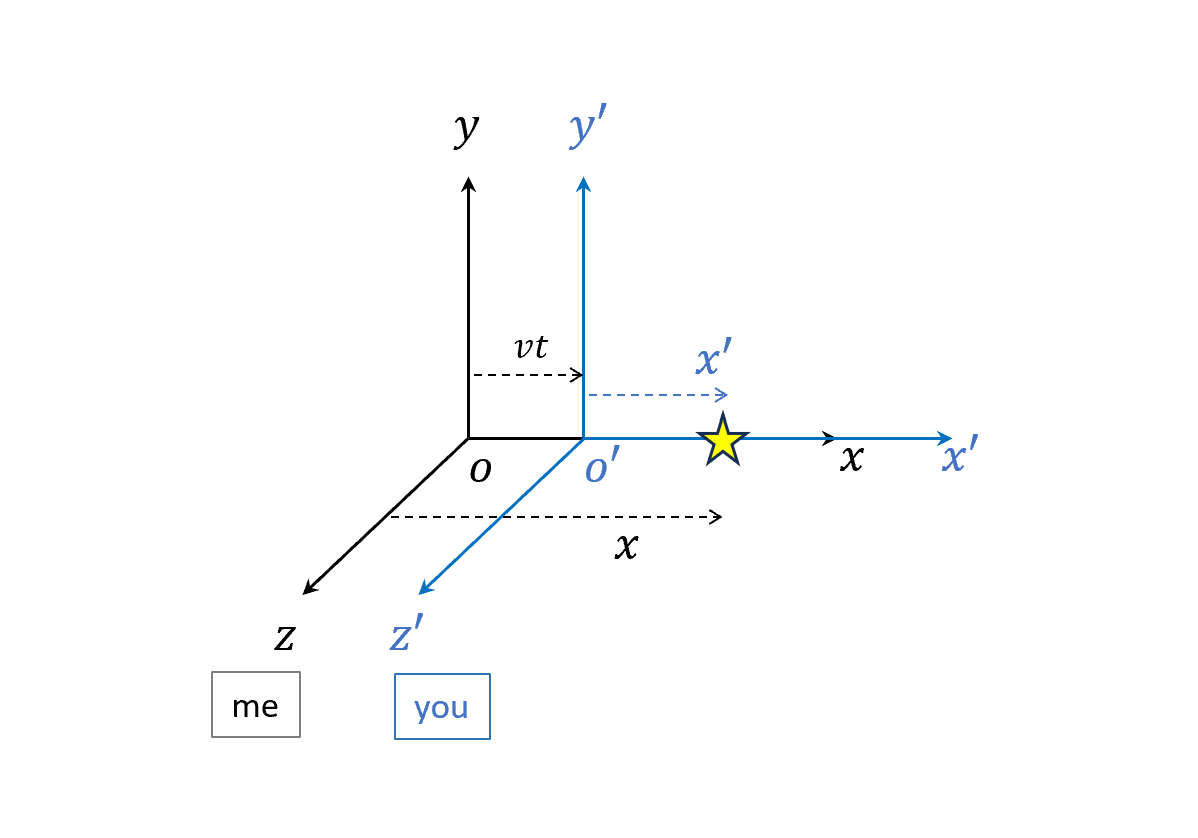
現在我們定兩個慣性座標系和兩個各自的慣性觀察者,黑色(我)和藍色(你)。
所謂的慣性,就是不受外力、沒有加速也沒有旋轉運動等等。
你和我的座標系在初始時原點$o$和$o’$重合,彼此之間只有一個相對速度$v$。
這時要先確認一件事情,老天對我們兩個座標系都是一視同仁的。
也就是說,在我的角度,看你是10m/s往前跑,換到你的角度,看我就是-10m/s遠離,而不是-15m/s遠離。
代表不論從哪一個座標系看,互相的相對速度相同,大自然並沒有比較偏好你或我,只要是慣性座標的觀察者,地位相等,沒有任何不同。
定義事件
現在在圖中打星星的地方發生了一個事件,譬如某個閃光。
但在繼續之前我們先來回顧一下「事件」的重要性。
假設我們今天想要測量一個物品的長度,若這個物品對我來說都不動,那我今天量頭(一個事件),明天量尾(一個事件),的確就能得到長度。
可是如果這個物品對我來說在動,我們就必需「同時」測頭測尾,就是量兩個事件,然後給出測量的位置(x,y,z)和時間(t),最後得到長度。
這裡更貼切的例子,譬如說一台火車,今天在台北,明天在花蓮,你總不能今天量車頭,明天量車尾,然後跟我說這台火車的長度一百多公里的荒謬結論吧!
我測量的事件
現在用我的尺,我的錶,想知道對於我來說,經過一段時間後,發生星星閃光事件時,該事件與你的距離長度。
看上圖就很簡單,向量的加減法得
\[x-vt\]你測量的事件
對於你來說,你用你的尺、你的錶,譬如說你開始在跑步,經過一段時間後,看到前方發生星星閃光事件時,該事件與你的距離長度。
一樣看上圖很簡單,就是
\[x'\]長度、時間轉換公式
這時我們經過反覆實驗,得出我量出來的距離長度,和你量出來的距離長度的轉換公式
\[x'\equiv\text{coordinate of event as measured by the primed frame}\\ =x-vt\]而量到的時間
\[t'=t\]兩者皆符合日常實驗結果和直覺想法,我跟你同一個起點,開始計時後(e.g., 10:00),我量到的星星閃光點,和你開始跑跑跑,跑到看到前面有星星閃光的時間點,會是一樣的(e.g., 10:05),然後我測到的該事件與你的距離,和你量到與你的距離會是一樣的。
這就是伽利略轉換公式了,將兩個不同慣性座標系描述一個事件的關係用公式表示出來。
速度轉換公式
現在有一個粒子,用均勻的速度沿著x軸從A點開始跑到B點,中間會發生無限個有位置和時間資訊的事件點,這時要算出這個粒子的速度,我們就取「兩個事件」,在我的座標系下就是$(t_1, x_1)$和$(t_2, x_2)$,所以速度
\[u_x\equiv\frac{x_2-x_1}{t_2-t_1}\]那該粒子對你來說呢?
無腦套用伽利略公式
\[\begin{align} u_x'&\equiv\frac{x'_2-x'_1}{t'_2-t'_1}\\ &=\frac{(x_2-vt_2)-(x_1-vt_1)}{t_2-t_1}\\ &=\frac{(x_2-x_1)-v(t_2-t_1)}{t_2-t_1}\\ &=u_x-v \end{align}\]Perfect!
這邊一樣要特別提醒一點:$u_x’$是你的尺你的錶量的,$u_x, v$是我的尺我的錶量的,本質上本來就沒有一定要一樣,但是在伽利略轉換的過程中,可以有這樣的關係式。
而這個關係式在我們日常生活中也反覆被驗證都是正確的。
與電磁學的衝突
按照伽利略轉換公式,如果我們今天是量一個光線
\[u_x'(\text{light}) = u_x(\text{light})-v\]伽利略得到的結果是:不同座標系,光線的速度會不同。
但這就開始與電磁學的結果發生衝突了!
不同慣性座標系的電磁實驗
一樣地,在我的慣性座標系下,若做電磁實驗滿足馬克示威方程式
\[\nabla\cdot\vec{E}=\frac{\rho}{\epsilon_0}\\ \nabla\times\vec{E}=-\frac{\partial \vec{B}}{\partial t}\\ \nabla\cdot B = 0\\ \nabla\times\vec{B}=\mu_0\vec{J}+\mu_0\epsilon_0\frac{\partial \vec{E}}{\partial t}\]那在你的慣性座標系下呢?
物理學在那時發展下來,普遍已確立電磁學是個fundamental theory,所以即便你跑到太空,你做的電磁實驗也要能滿足馬克示威方程式
\[\nabla'\cdot\vec{E'}=\frac{\rho'}{\epsilon_0}\\ \nabla'\times\vec{E'}=-\frac{\partial \vec{B'}}{\partial t'}\\ \nabla'\cdot B' = 0\\ \nabla'\times\vec{B'}=\mu_0\vec{J'}+\mu_0\epsilon_0\frac{\partial \vec{E'}}{\partial t'}\]注意這裡只有$\epsilon_0$和$\mu_0$沒有加prime,因為這只是個常數比例,在不同座標系間沒有差別都會一樣。
電磁波速、光速
假設我們現在在真空,所以定
\[\rho = 0\\ J = 0\]代進我的馬克士威方程推一下
\[\begin{align} \nabla\times(\nabla\times\vec{E})&=\nabla\times\left(\frac{\partial \vec{B}}{\partial t}\right)=-\frac{\partial}{\partial t}(\nabla\times\vec{B})\\ &=-\frac{\partial}{\partial t}(\mu_0 \epsilon_0)\frac{\partial \vec{E}}{\partial t}=-\mu_0 \epsilon_0 \frac{\partial^2\vec{E}}{\partial t^2}\\ &=\nabla(\nabla\cdot\vec{E})-\nabla^2\vec{E}\\ &\Rightarrow \nabla^2\vec{E}=\mu_0 \epsilon_0\frac{\partial^2 \vec{E}}{\partial t^2} \end{align}\]最後的公式就是波函式(wave equation),前面的係數就代表了波速,而電磁波就是光,所以光速
\[c=\frac{1}{\sqrt{\epsilon_0\mu_0}}\]只是常數組合出來的數值!
所以代進你的方程也得到一樣的結果,也是$c=\frac{1}{\sqrt{\epsilon_0\mu_0}}$。
衝突點
那不就跟我們前面的伽利略轉換公式有衝突了嗎?
按照伽利略對速度的轉換公式
\[u_x' = u_x-v\Rightarrow c = c\underbrace{-v}_{?}\]你也是c我也是c,這個轉換錯了?
到這裡,電磁學在進展到電磁波就是光之後來到了巔峰,牛頓力學則是在可預測未見天體的運動之後達到了巔峰,那麼兩者衝突到底誰對誰錯?還是都錯了?
這時候,愛因斯坦出現了!
他認為伽利略轉換應該要被修正,因為我們平常日常生活中,伽利略轉換公式是與實驗結果吻合的,但這裡和電磁學結合後有問題,光速的速度又非常快,所以認為伽利略轉換在討論「高速」的情況下要稍作修正。
