(2) 相對 ─ 勞倫茲轉換 Lorentz Transformation

修正因子$\gamma$

前面說到現在要來稍微修正伽利略轉換公式來處理我們碰到牛頓力學和電磁學結合時的衝突點。

可是要怎麼修正呢？

我們先回來看原本的這張圖

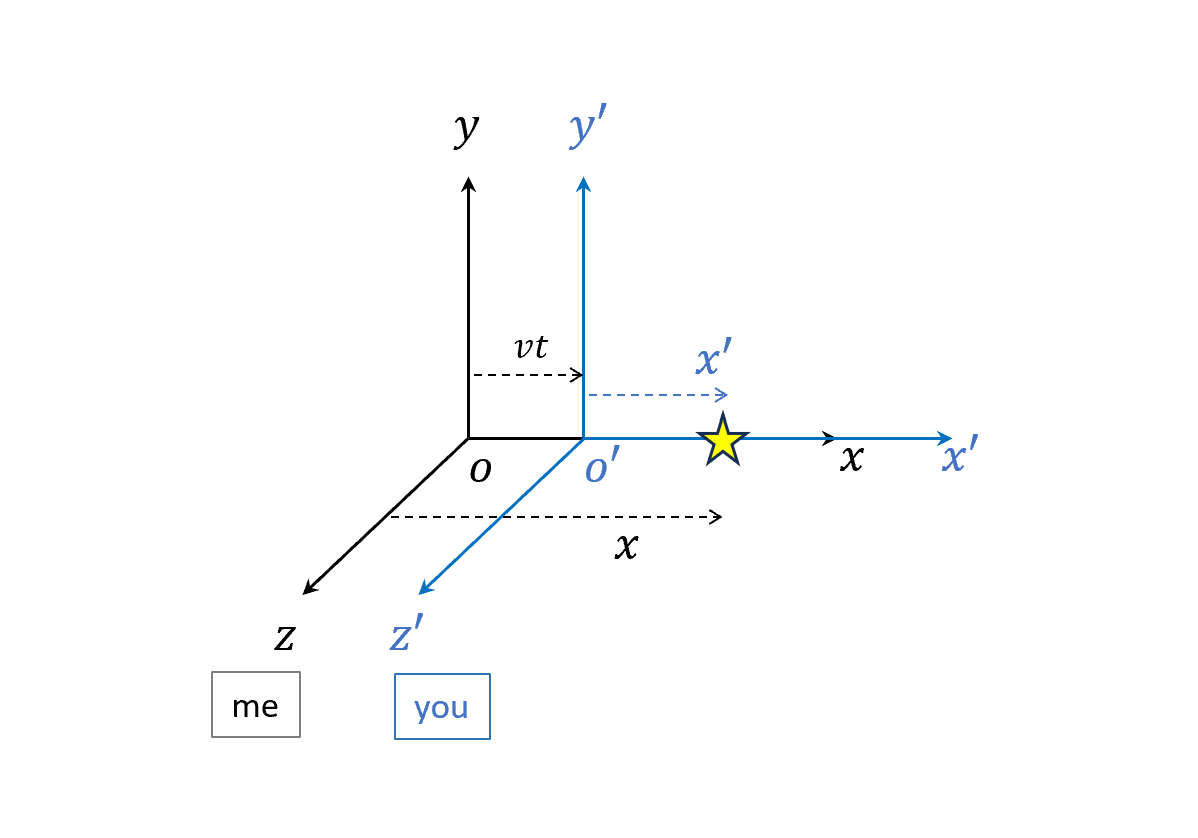
原本伽利略是這樣轉換的

\[x'=x-vt\]

可是前一章節我們一直有提到，$x’$是用你的尺量的，$x,v,t$則是用我的尺我的錶量的。

但很重要的一點是，你的量度和我的量度是一樣的嗎？

直白一點說，你的尺的一個刻度，等於我的尺的一個刻度嗎？

\[\text{black rule unit} \underbrace{=}_{?} \text{blue rule unit}\]

伽利略的世界裡是一樣的，但更general來說，畢竟是不同的，不一樣才更理所當然，一樣反而是特別的。

所以我們現在修改伽利略轉換公式，在前面引入新的因子$\gamma$

\[x'=\gamma (x-vt)\]

這個新因子會跟速度有關係，甚至更準確地說，是跟速率

\[|v|\]

有關係，跟方向無關。

至於時間，我們目前只能說

\[t\neq t'\]

因為我們不知道要怎麼引入其他的因子，若只是單純再寫是另外一個係數因子的倍數關係，那自由度就又太大了！

所以關於時間和空間的修正就先寫這兩條，然後稍微探討一下$\gamma$的特點。

特點

• 為什麼跟速度有關？

  因為若$v=0$，其實回到最上面的那張圖，你跟我沒有相對運動，那其實你=我，那也就不需要這個修正因子，所以一定要跟速度有關。

• 速度快慢的影響是什麼？

  如果是一般日常，探討的速度慢，那$\gamma\approx 1$，回到伽利略公式，也符合日常的實驗結果。但如果像是探討速度很快的光速，這個因子就不該再是1。

• 為什麼要說速率，不是速度？

  簡單回答，因為對稱性。如同前一節講的，老天對我們兩個座標系都是一視同仁的。在我的角度，看你是10m/s往前跑，換到你的角度，看我就是-10m/s遠離，而不是-15m/s遠離。 所以這個修正因子，跟方向(+-)無關，重點是我們之間的相對速率。 接下來會再細講這塊。

對稱性與時間修正

前面說到時間不知道要怎麼修正，我們可以從相對性原理(principle of relativity)出發。

相對性原理是在說，如果我們研究的物理定律是fundamental的話，那你看到和我看到的(都是慣性觀察者)形式，都要長一樣。譬如前一節舉到的電磁學，在你的座標和我的座標下，電磁學的馬克士威方程式都長一樣，只是看有沒有primed而已。

The “principle of relativity” says that all fundamental physical laws should appear to have the same form to all interial observers.

這也就隱含著對稱性的關係，所以我們其實改寫伽利略轉換的時候，也可以寫成這樣

\[x=\gamma(x'+vt')\]

注意只有速度的+-改了，因為對於你來說(相對於’座標)，我是往-v的方向跑走。

再看一次

\[\begin{cases} x'=\gamma(x-vt), \text{black}\to\text{blue}, \text{我看你以v跑走}\\ x=\gamma(x'+vt'), \text{blue}\to\text{black}, \text{你看我以-v跑走} \end{cases}\]

Perfect！

這不就是以前國中學的聯立方程式嗎！繼續開解！

\[\begin{align} t'&=\frac{\left(\frac{x}{\gamma}-x'\right)}{v}\\ &=\frac{\left(\frac{x}{\gamma}-(\gamma(x-vt))\right)}{v}\\ &=\gamma t-\frac{\left(\gamma-\frac{1}{\gamma}\right)}{v}x\\ &=\gamma\left(t-\left(\frac{1-\frac{1}{\gamma^2}}{v}\right)x\right) \end{align}\]

整理

\[\begin{cases} t'=\gamma\left(t-\left(\frac{1-\frac{1}{\gamma^2}}{v}\right)x\right)\\ x'=\gamma(x-vt) \end{cases}\]

時間修正項就出來啦！

可以看到他不是單純是什麼$t’=\alpha t$而已，還會跟$x$有關係！

而且因為我們從對稱性出發，所以不用再額外寫\(t=\cdots t', x=\cdots x'\)的公式了，只要把primed變成unprimed，速度+-互換就好，以後要換算很方便！

引入電磁學

推導到現在，\(x,t,x',t'\)代表的都可以是任意事件，任意一種物理的軌跡。

但前面電磁學說到，不論哪個座標系，光速只和常數有關係，在你的和我的座標系下光速都是一樣的，所以我們現在把這個公式引入描述光的軌跡，給出constraints

\[c=\frac{x_2'-x_1'}{t_2'-t_1'}=\frac{x_2-x_1}{t_2-t_1}\]

一樣地，光線上會有無數個事件，我們只是取兩個事件$(t_1,x_1), (t_2,x_2)$來寫出光速給出的限制條件。

這個限制條件就是為了讓我們可以修正第一節說的力學，使得其在電磁學也是對的。

求出$\gamma$值

那就繼續算囉！

\[\begin{align} c&=\frac{x_2'-x_1'}{t_2'-t_1'}\\ &=\frac{\gamma [(x_2-vt_2)-(x_1-vt_1)]} {\gamma\left[\left(t_2-\frac{1-\frac{1}{\gamma^2}}{v}x_2\right)-\left(t_1-\frac{1-\frac{1}{\gamma^2}}{v}x_1\right)\right]}\\ &=\frac{(x_2-x_1)-v(t_2-t_1)}{(t_2-t_1)-\left(\frac{1-\frac{1}{\gamma^2}}{v}\right)(x_2-x_1)}\\ &=\frac{\frac{x_2-x_1}{t_2-t_1}-v}{1-\left(\frac{1-\frac{1}{\gamma^2}}{v}\right)\cdot c}\\ &\Rightarrow \frac{1-\frac{1}{\gamma^2}}{v}c^2=v\\ &\Rightarrow 1-\frac{v^2}{c^2}=\frac{1}{\gamma^2} \end{align}\]

(這裡我們直接取正的，所以v很小的時候$\gamma$就會是1。)

\[\gamma = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\]

Lorentz Transformation

解出之後，代回去，以下的式子就是勞倫茲轉換

\[\begin{cases} t'=\gamma(t-\frac{v}{c^2}x)\\ x'=\gamma(x-vt)\\ y'=y\\ z'=z \end{cases}\]

with

\[\gamma = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\]

注意這裡因為速度只有在x方向，所以另外兩個方向就會是一樣的(也沒道理不一樣XD)。

速度的轉換

現在來看速度，在你的座標系

\[\begin{align} u_x' &= \frac{x_2' - x_1'}{t_2' - t_1'}\\ &= \frac{\gamma\left[(x_2 - vt_2) - (x_1 - vt_2)\right]}{\gamma \left[ \left(t_2 - \frac{v}{c^2} x_2 \right) - \left( t_1 - \frac{v}{c^2} x_1 \right)\right]}\\ &=\frac{(x_2 - x_1) - v(t_2 - t_1)}{(t_2 - t_1) - \frac{v}{c^2} (x_2 - x_1)}\\ &=\frac{u_x - v}{1 - \frac{v}{c^2}u_x} \end{align}\]

就是所謂的 Velocity Addition Theorem。

再來看另外兩個方向$y,z$，因為只有在$x$方向有相對速度，所以我們只推$y$，$z$方向是一樣的

\[u_y'\equiv\frac{y_2' - y_1'}{t_2' - t_1'} = \frac{y_2-y_1}{\gamma \left[(t_2-t_1)- \frac{v(x_2-x_1)}{c^2} \right]}\\ =\frac{u_y}{\gamma\left(1-\frac{vu_x}{c^2}\right)}\]

可以看到，因為時間的轉換和位置有關係，$x$方向的速度影響$y$方向的速度。

驗證：低速度近似回到伽利略轉換

假設相對速度很小

\[v \ll c\]

則

\[\gamma = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\approx 1\]

就可得伽利略的位置轉換公式。

\[x'\approx 1(x-vt)\]

而對於時間

\[t'\approx 1\left(t-\frac{v}{c^2}x\right)\]

看括號裡的項，可以拆成

\[\frac{v}{c}\cdot\frac{x}{c}\]

這時若假設發生的位置也相對來說很小

\[x \ll c\]

那麼兩個小小的項乘起來也還是小小的，所以忽略即可得伽利略的時間轉換公式

\[t'\approx t\]

對於速度，一樣拆成

\[\frac{v}{c}\cdot\frac{u_x}{c}\]

這時若假設particle在跑的速度相對來說很小

\[u_x \ll c\]

那麼兩個小小的項乘起來也還是小小的，忽略後分母只剩下1，也是原本伽利略的速度轉換公式。

\[u_x' = \frac{u_x - v}{1 - \frac{v}{c^2}u_x}\\ \approx u_x - v\]

驗證：光速

再稍微驗證回去，如果現在 particle 以 c 的速度在跑

\[u_x = c\]

則

\[u_x' = \frac{c - v}{1 - \frac{v}{c^2}c} = \frac{c-v}{1-\frac{v}{c}}=c\]

也是正確的！