(6) Small Oscillation ─ Example: Sympathetic Vibration
現在來看一個例子,兩顆粒子串接,中間接一個比較weak的彈簧。
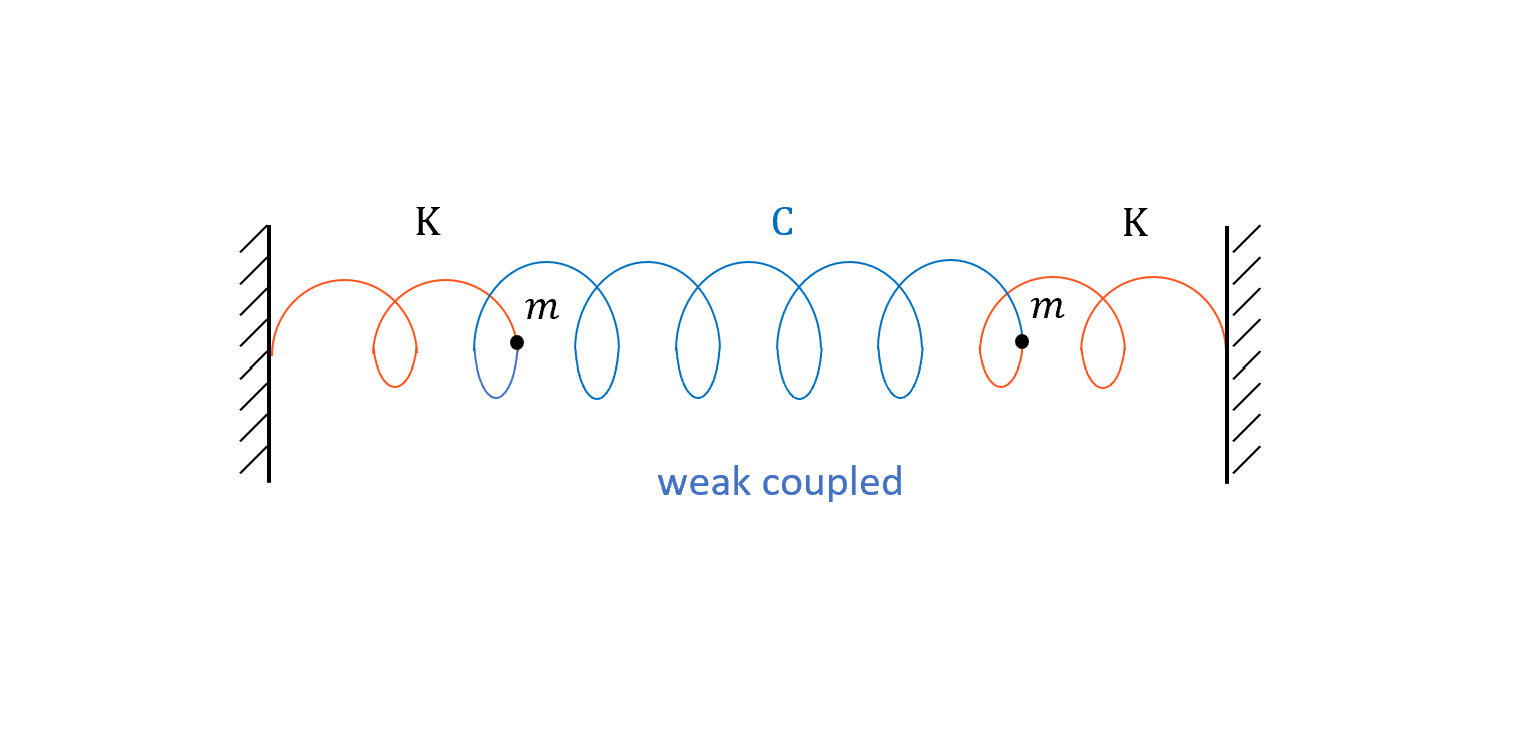
這個例子可以用很常見的實驗來做,擺兩張椅子,上面放一根棍子,棍子中間掛兩個一樣的小球,手動讓A小球開始晃,晃著晃著A會越來越慢,然後B會開始晃,過一段時間B會變慢,A再開始晃,稱這個為 Sympathetic Vibration。背後的原因當然是因為中間的棍子再被晃動的時候會有一些力矩,帶動另外一顆再晃,然後維持能量守恆情況下的結果。
EOM & Normal Modes
一樣來寫運動方程式吧!
兩顆粒子
\[\begin{cases} m\frac{d^2 x_1}{dt^2}=-Kx_1-C(x_1-x_2)\\ m\frac{d^2 x_2}{dt^2}=-Kx_2-C(x_2-x_1) \end{cases}\\ (C<<K)\]矩陣表示
\[\begin{pmatrix} m\omega^2-(K+C) & C\\ C&m\omega^2-(K+C) \end{pmatrix} \begin{pmatrix} x_1\\ x_2 \end{pmatrix} =\begin{pmatrix} 0\\ 0 \end{pmatrix}\\ \Rightarrow m\omega^2-(K+C)=\pm C\]求得兩個頻率解和對應的normal modes $(\xi, \eta)$
\[\begin{cases} \omega_1=\sqrt{\frac{K}{m}},\quad\begin{pmatrix}\xi\\\eta\end{pmatrix}\propto\begin{pmatrix}1\\1\end{pmatrix}\\ \omega_2=\sqrt{\frac{K+2C}{m}},\quad\begin{pmatrix}\xi\\\eta\end{pmatrix}\propto\begin{pmatrix}1\\-1\end{pmatrix} \end{cases}\]Time Evolution
那當然我們不是只是要算normal modes而已,noraml modes是限定特定初始狀態符合之後才會以這個方式運動,而真正我們想求的是time evolution,任意拉動造成的general情況都可以寫成normal modes的線性組合
\[\Rightarrow \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \end{pmatrix} (B_1 \cos \omega_1 t + B_2 \sin \omega_1 t) + \begin{pmatrix} 1 \\ -1 \end{pmatrix} (D_1 \cos \omega_2 t + D_2 \sin \omega_2 t)\\ (B_1, B_2, D_1, D_2: \text{determined by the initial conditions})\]而初始條件簡單起見,我們可以設左邊第一顆拉一個距離,沒有速度,第二顆則什麼都沒有,就像最前面說的 sympathetic vibration椅子的例子
\[x_1(0) = A \quad \dot{x}_1(0) = 0\\ x_2(0) = 0 \quad \dot{x}_2(0) = 0\]然後代進剛剛的線性組合公式
\[\begin{cases} A = B_1 + D_1 \\ 0 = \omega_1 B_2 + \omega_2 D_2 \\ 0 = B_1 - D_1 \\ 0 = \omega_1 B_2 - \omega_2 D_2 \end{cases}\]得到係數
\[B_1 = D_1 = \frac{A}{2}\\ B_2 = D_2 = 0\]再代回去
\[\Rightarrow \begin{cases} x_1(t) = \frac{A}{2} (\cos \omega_1 t + \cos \omega_2 t) \\ x_2(t) = \frac{A}{2} (\cos \omega_1 t - \cos \omega_2 t) \end{cases}\]現在有兩個$\omega$,也不知道傾向誰比較好,所以我們重新定義兩個變數
\[\overline{\omega} \equiv \frac{\omega_1 + \omega_2}{2} \\ \Delta \omega = \frac{\omega_1 - \omega_2}{2}\] \[\begin{align} \Rightarrow\omega_1 &= \overline{\omega} - \Delta \omega \\ \omega_2 &= \overline{\omega} + \Delta \omega \end{align}\]可以看到$\Delta\omega$和兩者的頻率差有關,但因為我們最前面假設過$C\ll K$,是weak coupling,所以兩者個頻率不會差太多,故而有
\[\Delta \omega \ll \overline{\omega} \\ (\because C \ll K)\]然後繼續用新的變數代回去
\[\begin{align} \Rightarrow x_1(t) =& \frac{A}{2} (\cos (\overline{\omega} - \Delta \omega)t + \cos (\overline{\omega} + \Delta \omega)t)\\ =& \frac{A}{2} (\cos \Delta \omega t \cos \overline{\omega} t + \sin \Delta \omega t \sin \overline{\omega} t\\ &+ \cos \Delta \omega t \cos \overline{\omega} t - \sin \Delta \omega t \sin \overline{\omega} t)\\ =& (A \cos \Delta \omega t) \cos \overline{\omega} t \end{align}\]一樣求$x_2$
\[x_2(t) = \frac{A}{2} (\cos (\overline{\omega} - \Delta \omega)t - \cos (\overline{\omega} + \Delta \omega)t) = (A \sin \Delta \omega t) \sin \overline{\omega} t\]公式解釋
可以看到
\[\begin{cases} x_1(t) = (A \cos \Delta \omega t) \cos \overline{\omega} t\\ x_2(t) = (A \sin \Delta \omega t) \sin \overline{\omega} t \end{cases}\]分析一下,因為$\Delta \omega \ll \overline{\omega}$,對於$x_1$來說,$(A \cos \Delta \omega t)$就是一個緩慢變化的振幅(slowly varying amplitude),$\cos \overline{\omega} t$就是快速的震動(fast vibration)。
所以系統一開始$t=0$的時候,振福為1,第一顆粒子快速振動,接著振福會慢慢變小,直到振到讓$\Delta \omega t = \pi / 2$的時候,振福為0,幾乎靜止了,隨後會再振起來。
而對於$x_2$也是一樣的,$t=0$,$(A \sin \Delta \omega t)$為0,所以一開始不會振,但隨著時間會開始振起來,直到$\Delta \omega t = \pi / 2$的時候,振福為1,是最大,並且用跟第一顆一開始的vibration頻率一樣,接著時間繼續走,又會慢慢靜止。
從這樣的公式就可以很清楚的看到sympathetic vibration的運動,起始時1動2不動,慢慢地1不動2動,最後再回來1動2不動!
When $t$ is near $t = \frac{\frac{\pi}{2}}{\Delta \omega}$ ($\Delta \omega$ “small” in some sense), the 1st oscillator is not vibrating significantly, and the energy is mostly transferred to oscillator 2. But if we wait even longer, up to $t = \frac{\pi}{\Delta \omega}$, then the energy is once again transformed back to oscillator 1.
General Case
這樣看會覺得前面的例子初始條件太刻意了,難道要這樣才會有sympathetic vibration?
所以我們現在把初始條件改一下,兩個粒子在一開始的時候都有任意的小擺動,看看 general 會怎麼樣。
\[x_2(0) = \text{small} \quad \dot{x}_2(0) = \text{small}\]代回去
\[\begin{cases} B_1 - D_1 = \text{small}\\ \omega_1 B_2 - \omega_2 D_2 = \text{small} \end{cases}\]得係數
\[\begin{cases} B_1\approx D_1\\ B_2\approx D_2 \end{cases}\](那當然對應的$x_1$的初始條件位置可能沒有拉得那麼滿,然後也有一點點速度。)
展開$x_2$
\[\begin{aligned} x_2(t) =&\quad(B_1 \cos \omega_1 t + B_2 \sin \omega_1 t) - (D_1 \cos \omega_2 t + D_2 \sin \omega_2 t)\\ =&\quad(B_1 \cos \omega_1 t - D_1 \cos \omega_2 t) + (B_2 \sin \omega_1 t - D_2 \sin \omega_2 t)\\ \\ =&\quad B_1 (\cos \Delta \omega t \cos \overline{\omega} t + \sin \Delta \omega t \sin \overline{\omega} t ) \\ &- D_1 (\cos \Delta \omega t \cos \overline{\omega} t - \sin \Delta \omega t \sin \overline{\omega} t ) \\ &+ B_2 (\cos \Delta \omega t \sin \overline{\omega} t - \sin \Delta \omega t \cos \overline{\omega} t )\\ &- D_2 (\cos \Delta \omega t \sin \overline{\omega} t + \sin \Delta \omega t \cos \overline{\omega} t ) \\ \\ =&\quad [(B_1 - D_1) \cos \Delta \omega t] \cos \overline{\omega} t \quad\quad\quad-(1)\\ &+ [(B_1 + D_1) \sin \Delta \omega t] \sin \overline{\omega} t \quad\quad\quad-(2)\\ &+ [(B_2 - D_2) \cos \Delta \omega t] \sin \overline{\omega} t \quad\quad\quad-(3)\\ &- [(B_2 + D_2) \sin \Delta \omega t] \cos \overline{\omega} t \quad\quad\quad-(4) \end{aligned}\]可以看到(1)和(3)都很小所以先不管。
(2)和(4)則一樣很明顯如果在一開始$\Delta \omega t \approx 0$,這兩項都會很小,然後時間繼續演化直到$\Delta \omega t\approx\frac{\pi}{2}$,那就會擺動變最大($x_1$就是相反)。
故而即便是General的初始條件,這個Sympathetic Vibration的現象還是在的!
物理解釋
到這裡我們進一步用物理來解釋這個現象,細想的話可以列出兩個奇怪的點
- 當第一顆粒子給能量給第二顆的時候,自己越振越小,那為什麼不是振到兩者能量一樣,達到平衡就好?就很像自己要沒錢的一窮二白了,還要繼續慷慨地給別人錢?
- 那給就給了,為什麼第二顆拿到全部能量之後,還會reverse回來給第一顆?然後一樣給到自己沒錢為止?
要解釋這個問題,我們先來看另外一個簡單的例子。
假設一個振子(oscillator)被外力用共振的頻率驅動
\[\frac{d^2 x}{dt^2}+x=D\cos t \quad\quad D>0\]這就很像Sympathetic Vibration中,因為中間有weak coupling,所以很像其中一顆用同樣頻率施力給另外一顆的想法。
然後設初始條件
\[\begin{cases} x(0)=0\\ \dot{x}(0)=-\mu_0,\quad\mu_0 > 0 \end{cases}\]簡單地解答,inhomogeneous + homogeneous的解
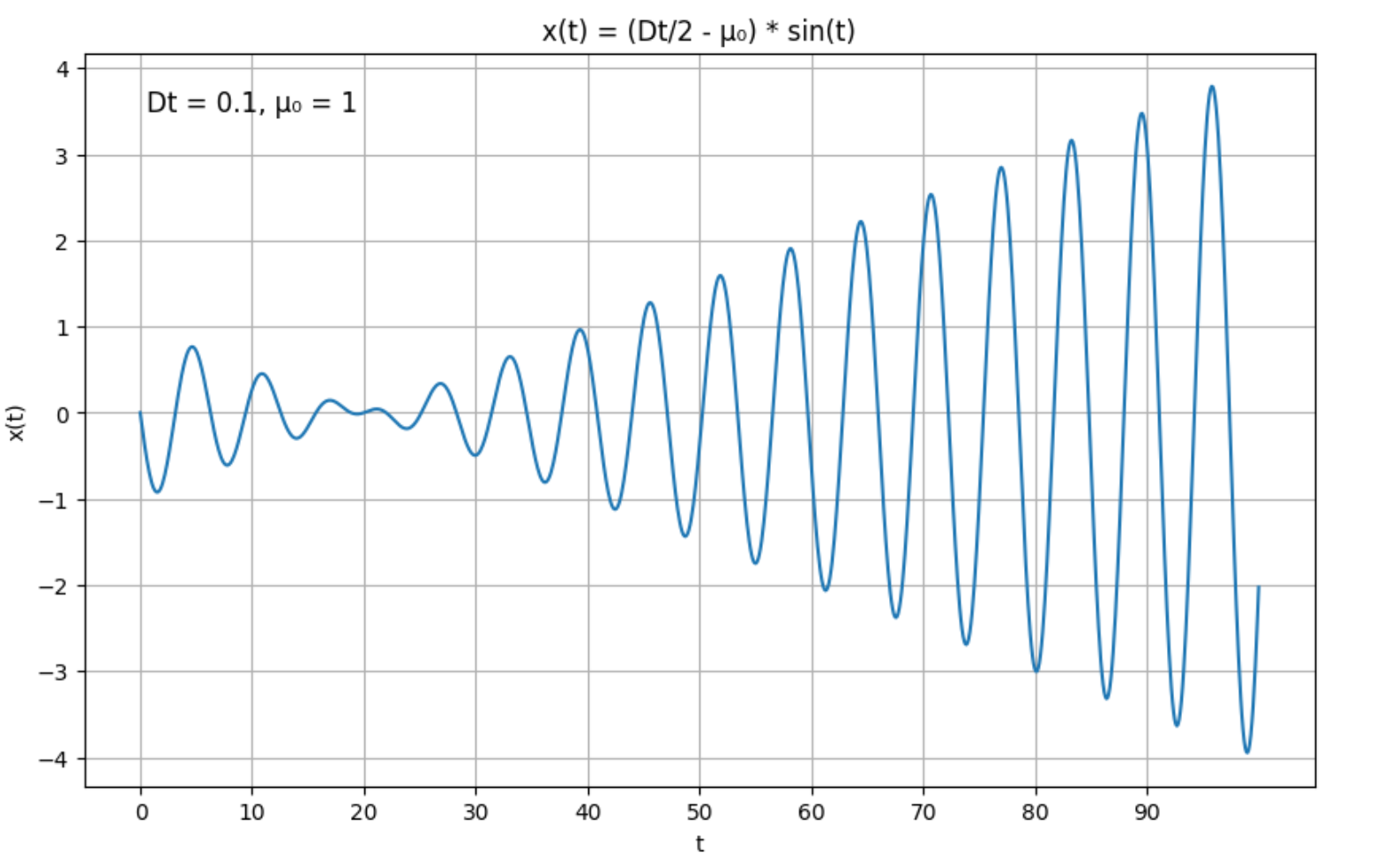
\[x(t)=\frac{D}{2}t \sin t+\alpha\cos t+\beta \sin t\](可以看到第一項inhomogeneous是secular term,類似於軌道pertubation theory提過的。)
繼續求
\[x(0)=0\Rightarrow \alpha = 0\\ \dot x(0)=-\mu_0\Rightarrow \beta=-\mu_0\\ \Rightarrow x(t)=\left(\frac{Dt}{2}-\mu_0\right) \sin t\]因為是weak coupling,所以可假設D很小,那麼括號振福這項$\left(\frac{Dt}{2}-\mu_0\right)$就一樣是緩慢隨時間變動的數值(slowly time-varying amplitude)。
接著討論兩個時間段的解
- $0\leq t\leq \frac{2\mu_0}{D}$: \(\bigg| \frac{Dt}{2}-\mu_0 \bigg|\) 會緩慢地減少,所以振福越來越小。
- $t > \frac{2\mu_0}{D}$: \(\bigg| \frac{Dt}{2}-\mu_0 \bigg|\) 會 無止盡地增加,振福越來越大!
我們可以畫個圖看一下
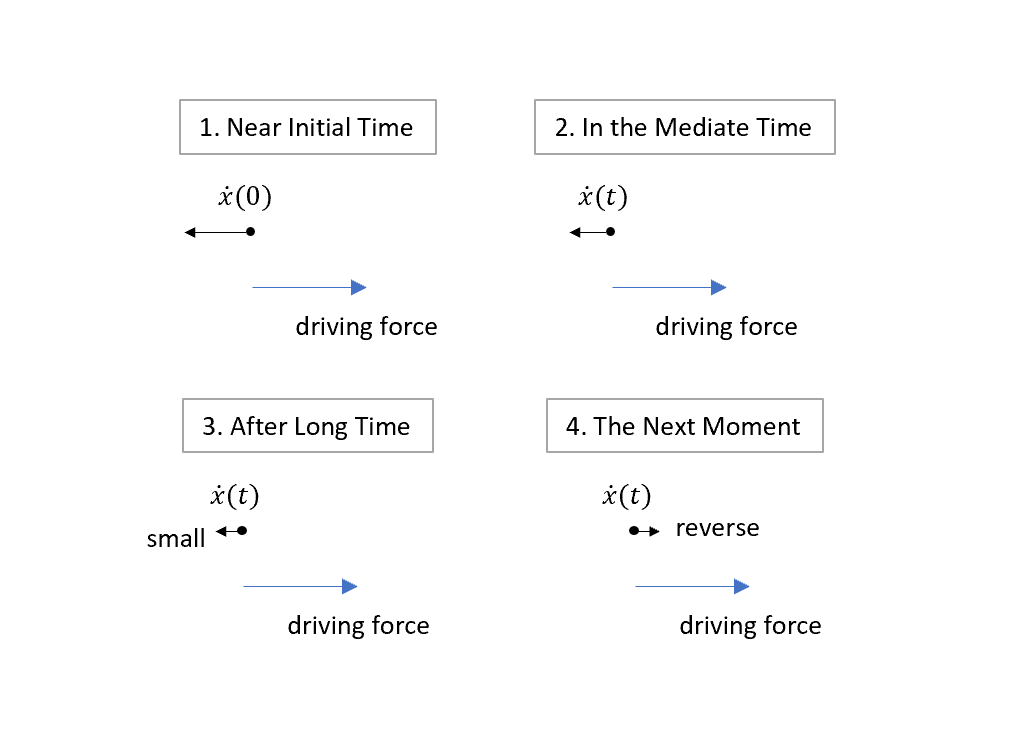
- 一開始速度向左($-\mu_0$),力向右($D>0)$,driving force 做負功(negative work)。
- 因為做負功,往左的速度當然就會變小。
- 時間越長越小。
- 經過臨界點,受driving force的影響,開始速度向右,並且從此無止盡。
一開始可能會覺得奇怪,一個系統跟他共振的話不是就是我一直pump能量給他讓他越來越大嗎?,但1~3的步驟告訴我們能量是越來越小的,這就像是幫人家推鞦韆,如果你要讓他停下來,他盪回來向你的時候,你會再給他推一點點(你給的就是他的自然頻率),他的速度就會自然慢下來了。所以共振是會讓系統的能量減小的!但當然你不能繼續,不然就會到第4步,他又會獲得能量越來越快。
Driving a system at the resonant frequency can decrease the energy of the system! But one should not keep doing it indefinitely。
現在回來Sympathetic Vibration,我們類比一下(第一顆叫P1,第二顆叫P2),這個粒子就是P1,然後driving force是P2給的(振得很快能量很大),所以跟P1共振的時候,會抽出P1的能量(1~3步),直到P1損失到0之後,就會開始從P2獲得能量(第4步),然後P2給的driving force當然不像這個簡單的例子保持constant一直給,所以P2的能量會一直縮小,直到損失到0之後,又會反過來從P1獲取能量。
簡單一點就是
- 2跟1共振。
- 以為1會獲得能量,但因為方向相反,所以1反而會減少能量。
- 1減到0,開始從2獲取能量。
- 1開始震動,變成1跟2共振。
- 2減少能量到0,開始從1獲取能量。
- 2跟1共振。
- 如此反覆變成 Sympathetic Vibration。
所以結合以上簡單的例子,我們來回答最一開始的問題,其實答案就是因為要Keeping the correct phase!
這個phase就是out of phase,因為兩者方向不同,就會一直保持著這個相位,不斷互相奪取又獲取能量,
最後補一張圖畫出$x(t)=\left(\frac{Dt}{2}-\mu_0\right) \sin t$,清楚看到反轉點之後顛倒爆噴的現象。