(3) 相對 ─ 勞倫茲轉換應用
一樣放剛剛的圖
Lorentz Transformation
統整一下,我們現在得出來的轉換公式
\[\begin{cases} t'=\gamma(t-\frac{v}{c^2}x)\\ x'=\gamma(x-vt)\\ y'=y\\ z'=z \end{cases}\]with
\[\gamma = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\]同時性
現在簡單來看一下,我們說的”同時”也是一個相對的概念,因為從轉換公式來看,現在時間在不同坐標系的轉換也跟距離有關。
假設在你的座標系(藍色)「同時」發生兩個事件$(t’, x_1’), (t’, x_2’)$,那麼在我的座標系(黑色)也會覺得這兩個事件是同時的嗎?
先說答案:不會同時。
證明:
(用對稱性的概念,+-換掉就好)
\[\begin{cases} t = \gamma \left( t' + \frac{v}{c^2} x' \right)\\ x = \gamma \left( x' + vt \right) \end{cases}\] \[t_2 - t_1 = \gamma \left[ \underbrace{(t_2' - t_1')}_{0} + \frac{v}{c^2} (x_2' - x_1') \right]=\gamma\frac{v}{c^2} (x_2' - x_1')\]這時若在你的座標系,發生事件的位置不同,假設
\[x_2' > x_1'\]那麼在我的座標系,看到的兩個事件就不是同時的,事件1會比事件2早發生
\[t_2 > t_1\]用長度定義時間
以前我們在解物理問題都說要同因次,所以在描述時間的時候,不太可能會說「經過一米的時間」,但我們現在來看一下,什麼叫做一寸光陰XD
首先我們知道速度乘上時間等於距離,那麼以通用的光速來說,經過一米需要的時間
\[c\Delta t = 1\Rightarrow \Delta t = \frac{1}{c} = \frac{1}{3}\times 10^{-8} (sec)\]有這樣的概念之後,我們重寫勞倫茲轉換,原本
\[\begin{cases} t' = \gamma \left( t - \frac{v}{c^2} x \right)\\ x' = \gamma \left( x - vt \right) \end{cases}\]全部同乘光速c
\[\begin{cases} ct' = \gamma \left( ct - \frac{v}{c} x\right) = \gamma ( ct - \beta x ) \\ x' = \gamma \left( x - \frac{v}{c} ct \right) = \gamma ( x - \beta ct ) \end{cases}\]看起來公式覺得很對稱!感覺可以在
\[\begin{pmatrix} ct' \\ x' \end{pmatrix}\]和
\[\begin{pmatrix} ct \\ x \end{pmatrix}\]間寫個linear transformation。
那我們開始吧!
矩陣形式
\[\begin{pmatrix} ct' \\ x' \end{pmatrix} = \gamma \begin{pmatrix} 1 & -\beta \\ -\beta & 1 \end{pmatrix} \begin{pmatrix} ct \\ x \end{pmatrix} = \mathbf{\hat{L}} \begin{pmatrix} ct \\ x \end{pmatrix}\]中間對稱的矩陣,不管那麼多,先來對角化
\[\begin{pmatrix} 1 -\lambda& -\beta \\ -\beta & 1-\lambda \end{pmatrix} \begin{pmatrix} \xi\\ \eta \end{pmatrix} = 0\]求得eigenvalue
\[(1-\lambda)^2-\beta^2 = 0\\ 1-\lambda=\pm \beta\\ \lambda = 1\mp\beta\]對應eigenvector
\[\lambda_1 = 1-\beta\Rightarrow \begin{pmatrix} \xi\\ \eta \end{pmatrix} \propto \begin{pmatrix} 1\\ 1 \end{pmatrix}\] \[\lambda_2 = 1+\beta\Rightarrow \begin{pmatrix} \xi\\ \eta \end{pmatrix} \propto \begin{pmatrix} -1\\ 1 \end{pmatrix}\]接著回到我們原始的vector
\[\begin{pmatrix} ct \\ x \end{pmatrix}\]任意的vector都可以寫成eigenvetor的線性組合,所以
\[\begin{pmatrix} ct \\ x \end{pmatrix} = a \begin{pmatrix} 1 \\ 1 \end{pmatrix} + b \begin{pmatrix} -1 \\ 1 \end{pmatrix}\] \[\begin{cases} ct=a-b\\ x=a+b \end{cases} \Rightarrow \begin{cases} a=\frac{ct+x}{2}\\ b=\frac{-ct+x}{2} \end{cases}\]統整並同理可得
\[\begin{pmatrix} ct \\ x \end{pmatrix} = \frac{ct+x}{2} \begin{pmatrix} 1 \\ 1 \end{pmatrix} + \frac{-ct+x}{2} \begin{pmatrix} -1 \\ 1 \end{pmatrix}\\ \begin{pmatrix} ct' \\ x' \end{pmatrix} = \frac{ct'+x'}{2} \begin{pmatrix} 1 \\ 1 \end{pmatrix} + \frac{-ct'+x'}{2} \begin{pmatrix} -1 \\ 1 \end{pmatrix}\]代進我們原本的勞倫茲矩陣形式
\[\begin{pmatrix} ct' \\ x' \end{pmatrix}= \mathbf{\hat{L}} \begin{pmatrix} ct \\ x \end{pmatrix}\]得
\[\frac{ct'+x'}{2} \begin{pmatrix} 1 \\ 1 \end{pmatrix} + \frac{-ct'+x'}{2} \begin{pmatrix} -1 \\ 1 \end{pmatrix} = \mathbf{\hat{L}}\left[ \frac{ct+x}{2} \begin{pmatrix} 1 \\ 1 \end{pmatrix} + \frac{-ct+x}{2} \begin{pmatrix} -1 \\ 1 \end{pmatrix} \right]\]先看等號右手邊,我們把$\frac{ct+x}{2}, \frac{-ct+x}{2}$ 當作兩個單純的數字,所以都提出來,然後把剛剛的eigenvalue帶進去($\gamma$也帶進去)
\[\because \mathbf{\hat{L}} \begin{pmatrix} 1 \\ 1 \end{pmatrix} = \lambda_1 \begin{pmatrix} 1 \\ 1 \end{pmatrix}, \quad\mathbf{\hat{L}} \begin{pmatrix} -1 \\ 1 \end{pmatrix} = \lambda_2 \begin{pmatrix} -1 \\ 1 \end{pmatrix}\] \[RHS = \frac{ct+x}{2}\gamma(1-\beta)\begin{pmatrix} 1 \\ 1 \end{pmatrix}+ \frac{-ct+x}{2}\gamma(1+\beta) \begin{pmatrix} -1 \\ 1 \end{pmatrix}\]比對一下等號左手邊
\[LHS = \frac{-ct'+x'}{2}\begin{pmatrix} 1 \\ 1 \end{pmatrix}+\frac{-ct'+x'}{2}\begin{pmatrix} -1 \\ 1 \end{pmatrix}\]對照一下就出現很漂亮的數學對應公式!
\[\begin{cases} ct'+x'=\gamma(1-\beta)(ct+x)\\ -ct'+x'=\gamma(1+\beta)(-ct+x) \end{cases}\]重寫勞倫茲轉換的好處
連續座標轉換
為什麼要多做這一步呢?
因為原本的公式
\[\begin{cases} t' = \gamma \left( t - \frac{v}{c^2} x \right)\\ x' = \gamma \left( x - vt \right) \end{cases}\]在時間轉換上,時間和位置是結合在一起轉的,所以一旦系統、座標複雜一些,或是有問題需要轉很多次,那這個公式就會很麻煩。
但如果我們把這兩個視作一個組合 $(ct+x)$!
這時候透過新的轉換方式
\[\begin{cases} ct'+x'=\gamma(1-\beta)(ct+x)\\ -ct'+x'=\gamma(1+\beta)(-ct+x) \end{cases}\]就很簡單的可以看到$(ct+x)$變成$(ct’+x’)$就是乘上一個倍數而已,想像一下若要轉很多次,那也不過只是這個倍數的N次方而已,相較之下就變得非常方便了!
舉例
舉個例子,我們把$\gamma(1+\beta)$合併,那
\[-ct'+x'=\gamma(1+\beta)(-ct+x)\\ \Rightarrow -ct'+x'=\sqrt{\frac{1+\beta}{1-\beta}}(-ct+x)\\ (\because \beta = \frac{v}{c}, \gamma=\frac{1}{\sqrt{1-\beta^2}})\]如果有第三個座標系,我們就一樣直接再轉一次
\[-ct''+x''=\sqrt{\frac{1+\beta'}{1-\beta'}}(-ct'+x')\]類似下面這張圖,所以可以很直接地得到第三個座標系和原本我們的座標系的關係
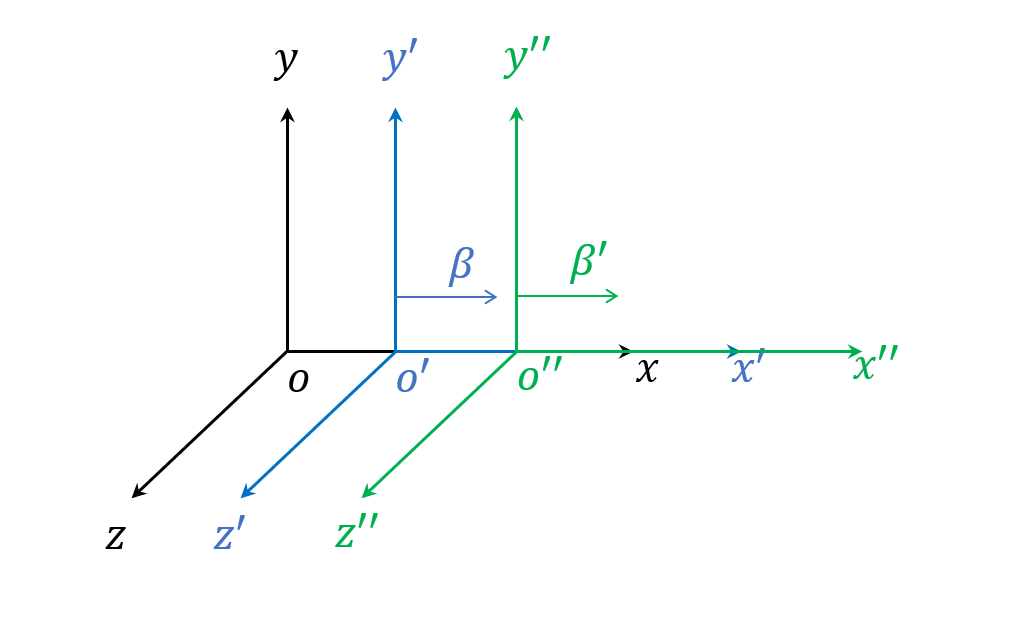
不管有幾個,反正就一直去用$\beta$的轉換倍數去換就好,這也是就是eigenvalue/eigenvector的數學好處,只要是在勞倫茲operator的eigenvector為基底之下,就是簡單地乘上倍數。
畢氏定理與不變量
可以很簡單的看出,等號左右各自相乘
\[\begin{cases} ct'+x'=\gamma(1-\beta)(ct+x)\\ -ct'+x'=\gamma(1+\beta)(-ct+x) \end{cases}\]會得到
\[\begin{align} (ct'+x')(-ct'+x')&=\gamma(1-\beta)(ct+x)\gamma(1+\beta)(-ct+x)\\ \Rightarrow (ct'+x')(-ct'+x')&= (ct+x)(-ct+x)\\ \Rightarrow -c^2t'^2+x'^2&=-c^2t^2+x^2 \end{align}\]不就很像我們學到的畢氏定理嗎!
最重要的是,我們知道$x\neq x’, t\neq t’$,因為各自是在自己的座標系看到的東西,但somehow經過這樣把時空一起組合的算法之後,會看到一個相等的不變量(invariant)在勞倫茲轉換裡面!
這樣的畢氏定理首先是由Minkowski(閔考斯基)注意到的,但畢氏定理常見是$a^2+b^2$,所以引入虛數的概念,將時空一起看,會寫成以下 $$ (ict')^2+x'^2=(ict)^2+x^2 $$ 在場論裡面,$ict, x$的確就是等價一起看的,但在接下來的筆記中,我們不會使用Minkowski's的寫法,而是用傳統重力派,雖然知道可以把時間空間攪和在一起看,但還是有先天的不同,所以會分開看。
"We will still single out time as something which has certain intrinsic feature distinct from that of space."
另外從簡單的從幾何上(把y軸視為t),我們也可以看到勞倫茲轉換就很像我們熟悉的「轉動 operator」(rotation in $\mathbb{R}^2$)
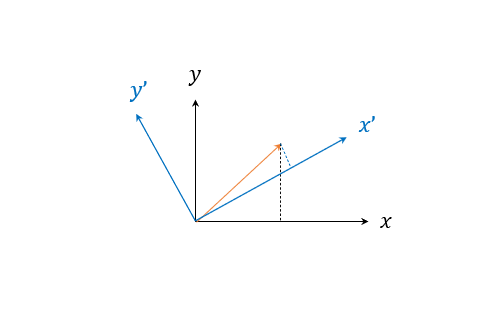
or 3-D space that coordinates do not have to be aligned
\[-c^2t'^2+x'^2+y'^2+z'^2=-c^2t^2+x^2+y^2+z^2\]最後公式形式(事件差)
至此,我們要再稍微改寫一下。
我們通常說的這個”invariant intervals”其實更準確地是在說「兩個」時空事件之間。
我們前三節都是用原點當作參考的第一個事件,而現在更通用地是要用「事件差」來表示
\[-c^2\Delta t'^2+\Delta x'^2+\Delta y'^2+\Delta z'^2=-c^2\Delta t^2+\Delta x^2+\Delta y^2+\Delta z^2\\ \Rightarrow -c^2dt'^2+dx'^2+dy'^2+dz'^2=-c^2dt^2+dx^2+dy^2+dz^2\]我們把這個當作是某種距離的平方(a sort of distance squared),不能完全算是距離,因為有個負號,若此不變量是正的,比較是空間的概念,若是負的,則比較是時間的概念。
總而言之,寫成事件差的形式,並把這個相等的不變量當作一種測度”measure or metric”。
