(4) 相對 ─ 長度收縮及時間膨脹
複習一下勞倫茲轉換公式
\[\begin{cases} ct' = \gamma ( ct - \beta x ) \\ x' = \gamma ( x - vt ) \end{cases}\]然後一樣現在定兩個座標系
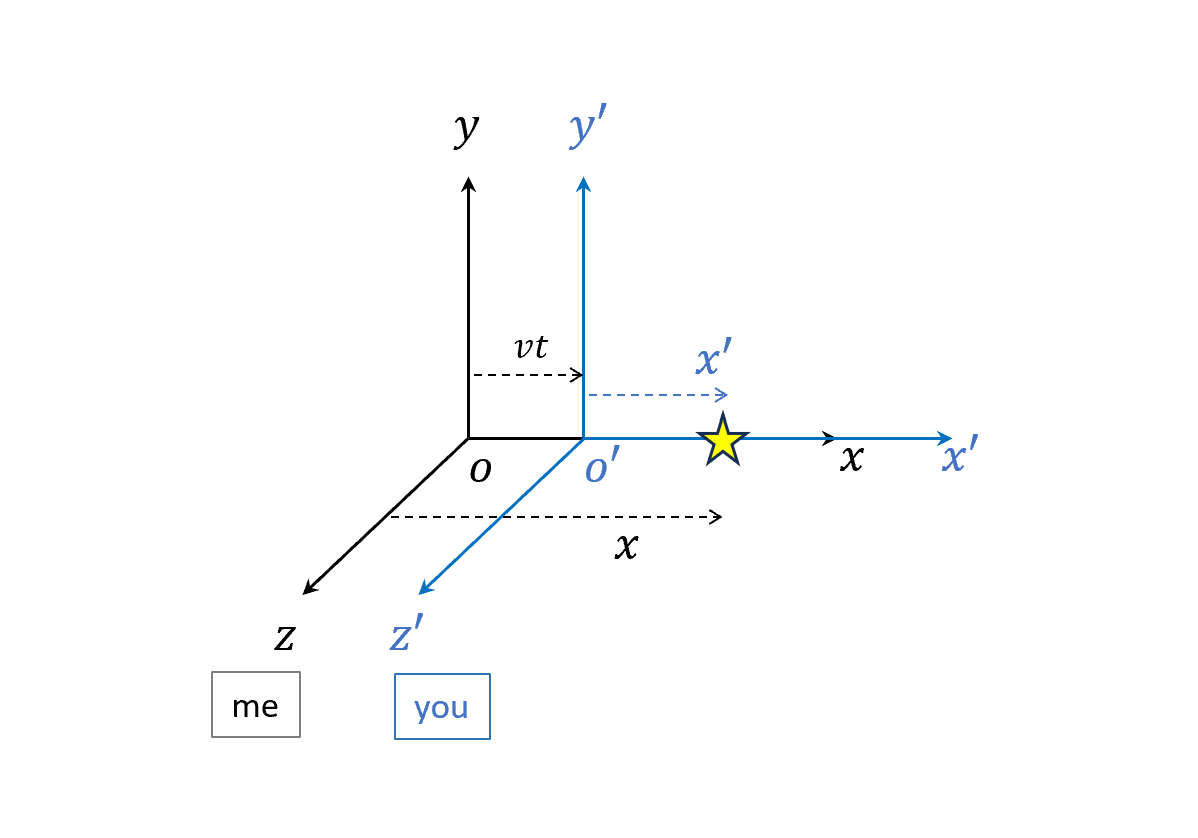
現在我們來計算黑色座標系看藍色座標系的物體及時間體感的差別。
長度收縮
Proper Length
首先先來定義Proper Length的意思:對於慣性座標系的觀察者來說,測量靜止物體的長度。
The length measured by an inertial observer to whom the object is at rest.
這裡的”Proper”就是本身自己具有的數值(eigenvalue的概念)。
我們將這個長度標誌為$L_{proper}$
測量長度的兩個事件
現在你帶著一個尺在跑(藍色坐標系),那我(黑色座標系)會怎麼測量你的尺呢?
- 定義兩個事件:量尺的左端 及 量尺的右端。
- 定義測量長度:對測量的座標系來說,「同時」測量這兩個事件。(測量長度當然一定是同時去測,你不可能在人一歲的時候先量腳底,二十歲的時候再量頭)
所以現在測量長度的限制在於我,必須同時測量兩端,因此寫下兩個事件,並假設尺的左端在我的原點。
\[\begin{cases} (t_1, x_1)=(0, 0)\\ (t_2, x_2)=(0, L) \end{cases}\]這裡的$L$就是我測量在運動中物體的長度。
勞倫茲轉換
接下來就無腦做轉換
\[ct_1' = \gamma ( ct_1 - \beta x_1 ) = 0\\ x_1' = \gamma ( x_1 - vt_1 ) = 0\] \[ct_2' = \gamma ( ct_2 - \beta x_2 ) = -\beta \gamma L\\ x_2' = \gamma ( x_2 - vt_2 ) = \gamma L\]相減
\[t_2' - t_1' = -\frac{\beta}{c}\gamma L\\ x_2' - x_1' = \gamma L = L_{proper}\]得到我測量的運動中物體的長度
\[L = \frac{L_{proper}}{\gamma}\]其中$\gamma > 1 $,所以
\[L < L_{proper}\]代表我測量運動中的物體長度會比較短:長度收縮
那時間呢?看起來也有差值?
但對你(移動中的)來說其實沒差,頂多覺得我這兩個事件不是在同時間進行測量,但你也不用管我在幹嘛,你只測量對你來說靜止尺的proper length。
時間膨脹
Proper Time
定義Proper Time的意思:對於慣性座標系的觀察者來說,測量同一位置上的時間「滴」、「答」兩個事件。
The time elapsed between two ticking events of a clock at rest in the measuring (inertial) frame.
我們將這個時間標誌為$T_{proper}$
測量時間的兩個事件
現在移動中的你(藍色坐標系)的滴答時間,我(黑色座標系)會感覺多久?
- 定義兩個事件:時間滴 及 答。
- 定義測量時間:對測量的座標系來說,「同位置」測量這兩個事件。
所以現在測量時間的限制在於你,同位置下寫下兩個事件,並假設位置都定在你的原點。
\[\begin{cases} (t'_1, x'_1)=(0, 0)\\ (t'_2, x'_2)=(\tau, 0) \end{cases}\]這裡的$\tau$就是你測量的$T_{proper}$。
勞倫茲轉換
接下來就無腦做轉換
\[ct_1 = \gamma ( ct'_1 + \beta x'_1 ) = 0\\ x_1 = \gamma ( x'_1 + vt'_1 ) = 0\] \[ct_2 = \gamma ( ct'_2 + \beta x'_2 ) = \gamma c \tau\\ x_2 = \gamma ( x'_2 + vt'_2 ) = \gamma v \tau\]相減
\[t_2 - t_1 = \gamma \tau = \gamma T_{proper}\\ x_2 - x_1 = \gamma v \tau\]得到我測量運動中時間滴答兩下經過的時間
\[T = \gamma T_{proper}\]其中$\gamma > 1 $,所以
\[T > T_{proper}\]代表我測量運動中時間滴答兩下經過的時間比較久:時間膨脹
(對你來說滴答只有一秒的話,對我來說已經十年,倒過來講就會講運動中的時間走得比較慢,想想星際效應Cooper在第一個星球的一小時,女兒在地球已過23年QQ)
那距離呢?看起來也有差值?
一樣地,對我來說沒差,你在同位置的滴答兩下,但對我來說你(時鐘)位置有變(在運動),如此而已。
