(5) 相對 ─ 時空圖
現在我們重新畫時空的幾何圖,前面說看起來很像是一般的旋轉圖,但因為時間項有負號,所以其實會長得不太一樣。
我們就一起來看,若把x一樣當x軸,ct當y軸,x’軸和ct’軸應該會是什麼樣子。
Spacetime diagram
一樣先列出勞倫茲轉換矩陣形式
\[\begin{pmatrix} ct' \\ x' \end{pmatrix} = \gamma \begin{pmatrix} 1 & -\beta \\ -\beta & 1 \end{pmatrix} \begin{pmatrix} ct \\ x \end{pmatrix}\]x’-axis
x’-axis 就是所有 t’=0 的點,而 t’=0 又代表
\[ct-\beta x = 0\\ ct=\beta x\]代表相對於x軸是一個斜率為$\beta$的直線。
ct’-axis
ct’-axis 就是所有 x’=0 的點,而 x’=0 又代表
\[-ct\beta+x=0\\ x=\beta(ct)\]代表相對於ct軸,也是一個斜率為$\beta$的直線。
那麼最後畫出來就長這樣啦!
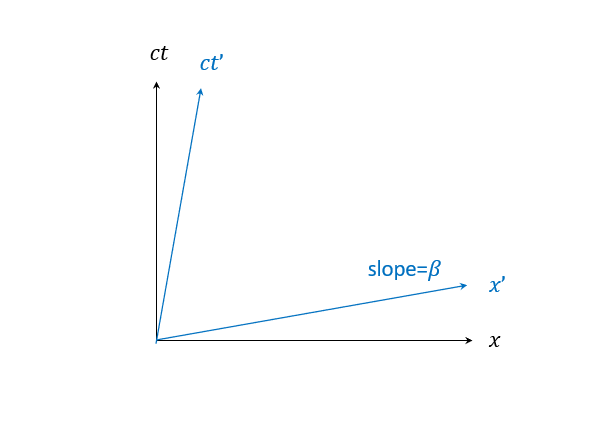
可以看到新的兩個軸都是往內擠的!
(不像一般的旋轉是一起向右或向左轉某個角度,但當然還是可以用特別的方法變成一般旋轉的幾何圖,這裡不多做討論)。
長度收縮
前一章節講到的長度收縮,我們也可以用時空圖來看。
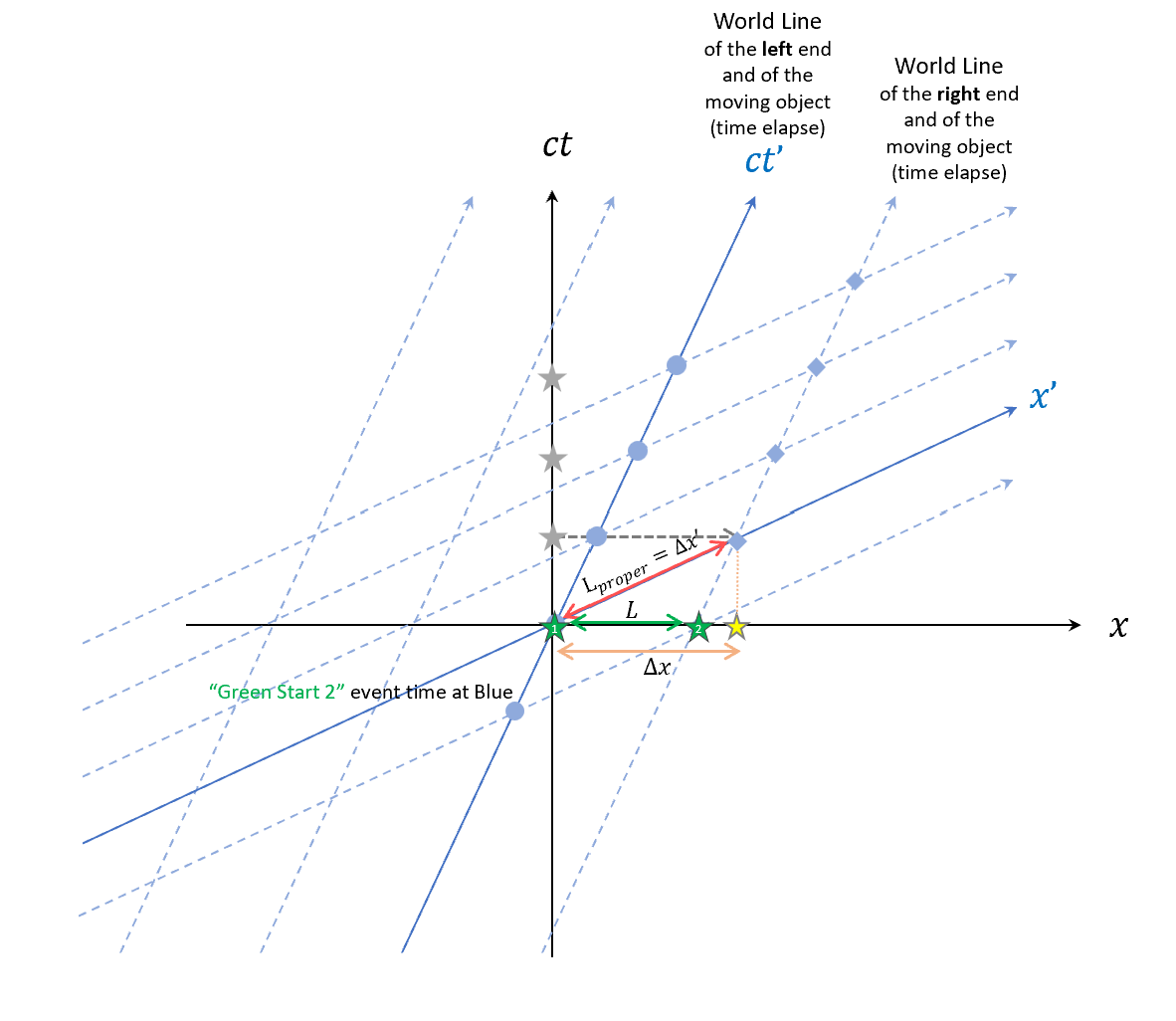
World Line
藍色座標系
畫兩個生命線(World Line),分別是藍色座標系下尺的 左端 和 右端 的生命線,對於 x’ 來說都維持在各自的位置,但是時間一直在往前走,如圖中的藍圈和藍菱形。
黑色座標系
對於黑色座標系,也有自己的時間在跑,如灰色星星。
尺的長度
藍色座標系
對藍色來說,在時間為0的時候,量到的尺的proper length($L_{proper}$),就是尺的左右兩端,圖中為紅線長度。
黑色座標系
同樣從時間為0開始測量,因為測量長度要「同時」,所以對黑色來說,原點測量尺的左端(綠星1),然後在維持時間 = 0的情況下往右畫線,直到和藍色右端的World line相交,就代表黑色看到並記錄(綠星2),此時
綠線就是黑色測量到的尺的長度L。
換算一下的確 $L = L_{proper} / \gamma$
時間
前面章節在算的時候,有得到
\[t_2' - t_1' = -\frac{\beta}{c}\gamma L\]從這張圖也可以看得出來,對於藍色來說,綠星2的事件發生的時間比綠星1還要早,所以藍色覺得黑色是「先量右再量左」,但黑色自己是「同時」量左右的。
Minkowski公式
\[-c^2 \Delta t'^2+\Delta x'^2=-c^2 \Delta t^2+\Delta x^2\]若假設 $L_{proper} = \Delta x’ $定義為1單位,然後$c^2 \Delta t^2$ 我們從斜率算知道是 $\beta^2 \Delta x^2$,所以
\[\Rightarrow -c^2 \cdot 0 + \Delta x'^2=-(\beta \Delta x)^2+\Delta x^2\\ \Rightarrow \Delta x' = \sqrt{(1-\beta^2)}\Delta x\]得到
\[\Delta x' = 1 = L_{proper},\quad \Delta x > 1= L_{proper}\]$\Delta x$ 在圖中就是投影到 x 軸的黃星與原點的長度 (橘線),重點有兩個
- $\Delta x$並不是黑色量到的尺長度!
- $\Delta x > \Delta x’ $ 是正確的,雖然一般圖看起來 紅線 > 橘線,但因為計算的公式時間部份是負的,所以的確 橘線 > 紅線。
那這樣$\Delta x$ (黃星) 代表啥意義呢?
沒有意義。
若真的要硬講的話,黃星就是黑色在過了一段時間後(第一個灰星),去量看到的尺右端,然後標記下來。
可是這沒啥意義,黑色在時間0測量尺左端標記為綠星1,時間t測量尺右端標記為黃星(往右畫到尺右端的world line),然後計算黃星和綠星的差距,沒有意義。
就很像你一歲的時候量嬰兒的腳底,等他二十歲的時候量他的頭頂,要幹嘛?
小結
- 紅線:藍色量的Proper Length
- 綠線:黑色量的長度,比 Proper Length 短(長度收縮)。
- 同時性:對黑色來說,同時量左右。對藍色來說,先量右再量左。
- 橘線:Minkowski 公式得出來的,沒有長度意義,只是單純代表座標。
- 橘線長度 > 紅線長度。
時間膨脹
時間同理,畫圖
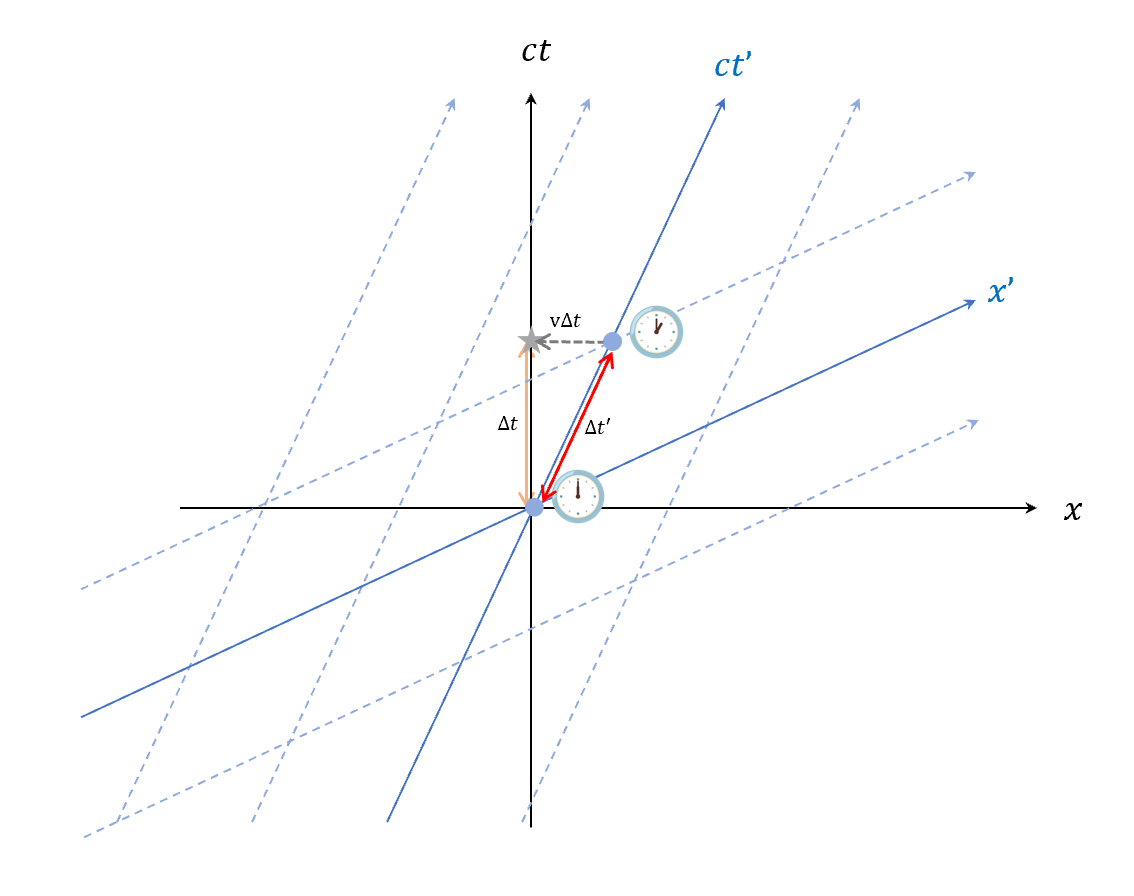
不過現在時鐘只有一個,生命線就一條,在一直在固定位置,藍色計算滴~答兩個事件的時間(紅線),定義為一個單位。
對黑色來說,時鐘從原點跑掉了,知道時鐘有在運動($v\Delta t$)。
然後投影到黑色的灰星上,對黑色來說舊是量到的時間長,就是橘線。
(簡單來說就是黑色往右畫線與藍色時鐘生命線發生「答」事件相交時經過的時間。)
Minkowski 公式
時間膨脹直接來看公式就好,一樣
\[-c^2 \Delta t'^2+\Delta x'^2=-c^2 \Delta t^2+\Delta x^2\]若假設 $T_{proper} = \Delta t’ $定義為1單位,然後$\Delta x$ 我們從斜率算知道是 $\beta c \Delta t$,所以
\[\Rightarrow -c^2 \Delta t'^2 + 0=-c^2 \Delta t^2+(\beta c \Delta t)^2\\ \Rightarrow -c^2 \Delta t'^2 =-c^2 \Delta t^2+(v \Delta t)^2\\ \Rightarrow (c^2-v^2)\Delta t^2 = c^2\Delta t' ^2\]得到
\[\Delta t' = 1 = T_{proper}\\ \Delta t > 1 = T_{proper}\]所以囉~橘線 > 紅線,藍色的一小時,黑色可能幾十年。
光錐
現在來畫光線的world line,因為速度是光速所以$\beta = 1$,所以就是45度斜率的線,反方向跑就是-45度。
從過去到現在畫出來如下圖,我們稱這個為光錐(light cone)。
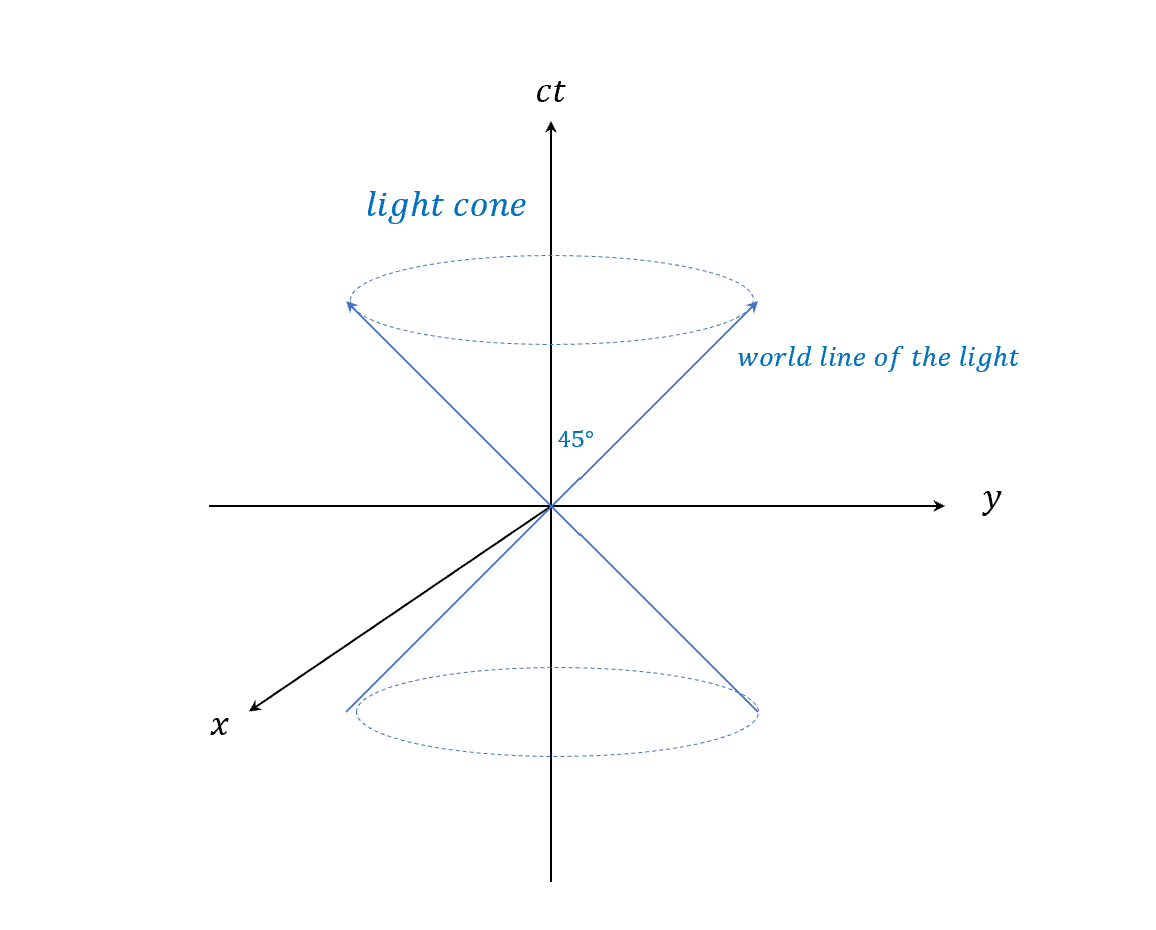
接著來看一件事情,假設我們座標系中有一個實質物體在加速運動,我們可以取特定時間的瞬間速度v,然後找一個慣性座標系也剛好以v在移動的朋友(primed frame),這個實質物體對朋友來說瞬間是靜止的(位置不變),這時我們來算proper time$(\tau)$
\[-c^2 dt'^2+dx'^2+dy'^2+dz'^2=-c^2 dt'^2+0+0+0\\ =-c^2 dt^2+dx^2+dy^2+dz^2\] \[\Rightarrow dt' = d\tau = \sqrt{\frac{c^2dt^2-(dx^2+dy^2+dz^2)}{c^2}}\\ =dt\sqrt{1-\frac{1}{c^2}\left[\left(\frac{dx}{dt}\right)^2+\left(\frac{dx}{dt}\right)^2+\left(\frac{dx}{dt}\right)^2\right]}\] \[\tau = \int dt\sqrt{1-\frac{u^2}{c^2}},\quad u:\text{speed of object}\]算到這裡其實代表心裡有一個基本假設,運動的實質物體速度要小於光速
\[u < c\]這個假設的精神是:如果一個物質實體,有個特性是在運動的過程中,隨時都有辦法可以找到一個慣性坐標系的觀察者去看他,並且對該觀察者來說瞬間速度是0,那我們就預期這個物質實體不能超過光速。 而這也是我們目前世上大部分做實驗找到的物體限制。
邏輯上來說,也就代表若怎麼都找不到這樣的慣性座標系去看他是靜止的,就沒有道理此物質實體會限制不能超過光速。
像是光本身,因為沒有辦法找到任何的慣性座標系使得光速為0(任何座標系去看都是c),所以光本身就不受此限制(電磁波就不受此限制)。
當然地,或許世上也有東西沒有辦法找到任何慣性座標系使得其速度為0,那這個東西就可以超過光速,只是目前還沒有找到。
