(6) 相對 ─ 都普勒效應
聲波的都普勒效應我們很熟悉,現在來看光線的都普勒效應。
Longitudinal:觀察者與波源移動方向平行
假設有靜止的觀察者座標系(黑色),和以速度v在移動的座標系(藍色)。
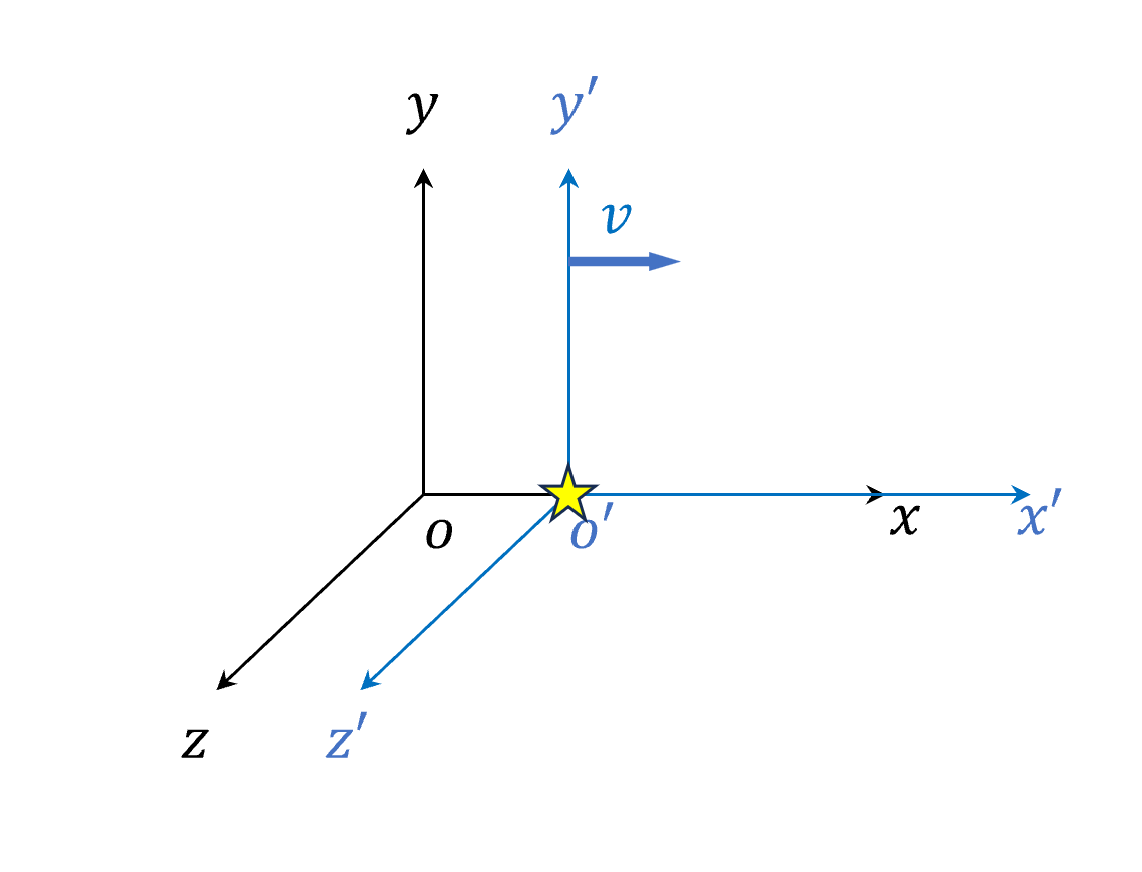
現在定義在移動坐標系的兩個的光線發射事件:
\[\begin{cases} (t_1', x_1') = (0, 0)\\ (t_2', x_2') = (\Delta t', 0)\\ \end{cases}\]分別為在原點的第一次發射,和經過時間$\Delta t’$後第二次發射。 並且對於藍色座標系來說,兩次發射都是同個位置(原點)。
在黑色座標系下,做勞倫茲轉換
\[\begin{cases} ct_1=\gamma(ct_1'+\beta x_1')=0\\ x_1 = 0\\ ct_2=\gamma(ct_2'+\beta x_2')=\gamma c \Delta t'\\ x_2 =\gamma(x_2'+\beta c t_2')=\gamma \beta c \Delta t' \end{cases}\]接收端時間差
黑色座標系下的接收端在$x = L$,如圖
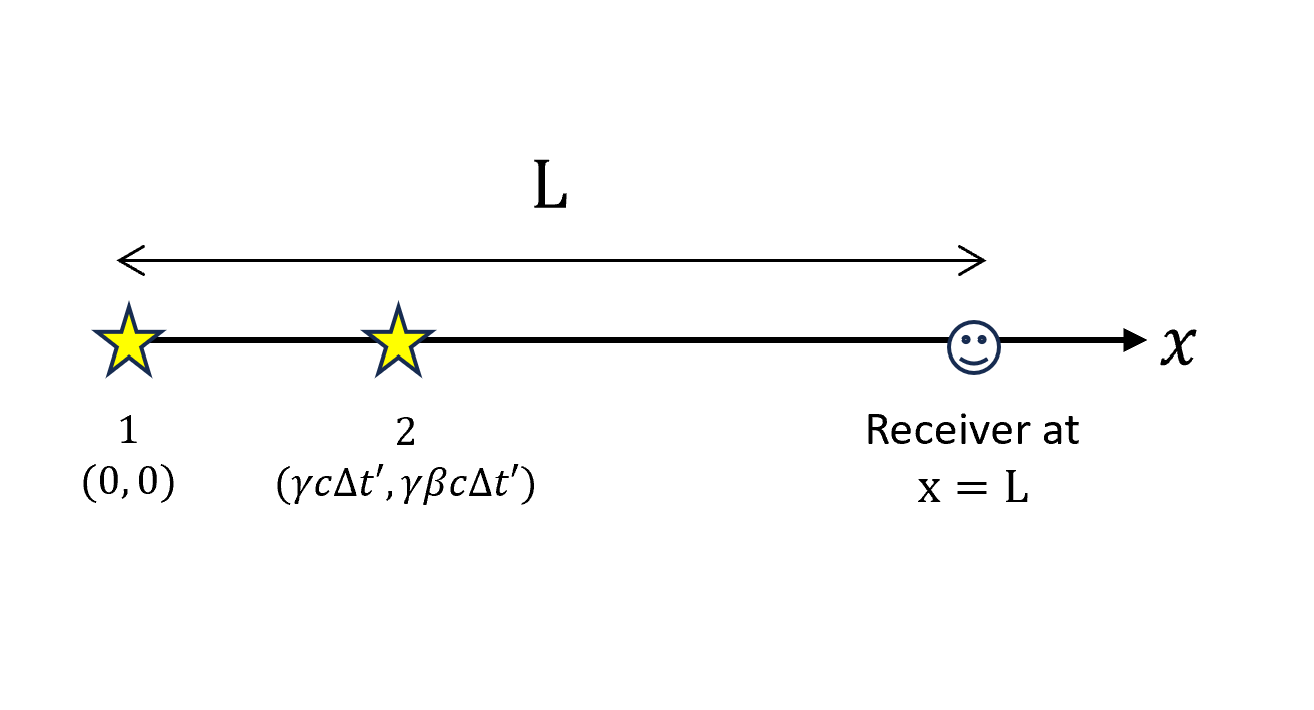
所以兩次收到的事件,收到的時間各自為
\[\begin{cases} T_1 = \frac{L}{c}\\ T_2 =\frac{L-x_2}{c}+t_2=\frac{L-\gamma \beta c \Delta t'}{c}+\gamma \Delta t' \end{cases}\]得到兩個事件時間差
\[T_2-T_1=\gamma \Delta t'(1-\beta)\]接收端頻率
換算頻率
\[\frac{1}{f_{observed}}=T_2-T_1=\gamma(1-\beta)\frac{1}{f_{emission}}\\ \Rightarrow f_{observed}=f_{emission}\times\frac{1}{(1-\beta)\gamma}=\frac{\sqrt{1-\beta^2}}{(1-\beta)}f_{emission}\\ =\sqrt{\frac{1+\beta}{1-\beta}}f_{emission}, \quad \sqrt{\frac{1+\beta}{1-\beta}} > 1\]證明若波源逐漸靠近接收端,光波會被壓縮,頻率變大。
反方向同理,若波源遠離,光波被拉長,頻率變小
\[f_{-observed}=\sqrt{\frac{1-\beta}{1+\beta}}f_{emission}\]這個都普勒效應就是單純的波被壓縮/拉長的結果。
Tranverse:觀察者與波源移動方向垂直
現在來看與波源運動方向垂直的都普勒效應,感覺應該不會有都普勒效應,因為對接收端來說波不會拉長會壓縮,但因為在運動的物體時間慢(time dilation),所以接收端還是會感受到頻率的差異。
假設有靜止的觀察者座標系(黑色),和以速度v在移動的座標系(藍色)。
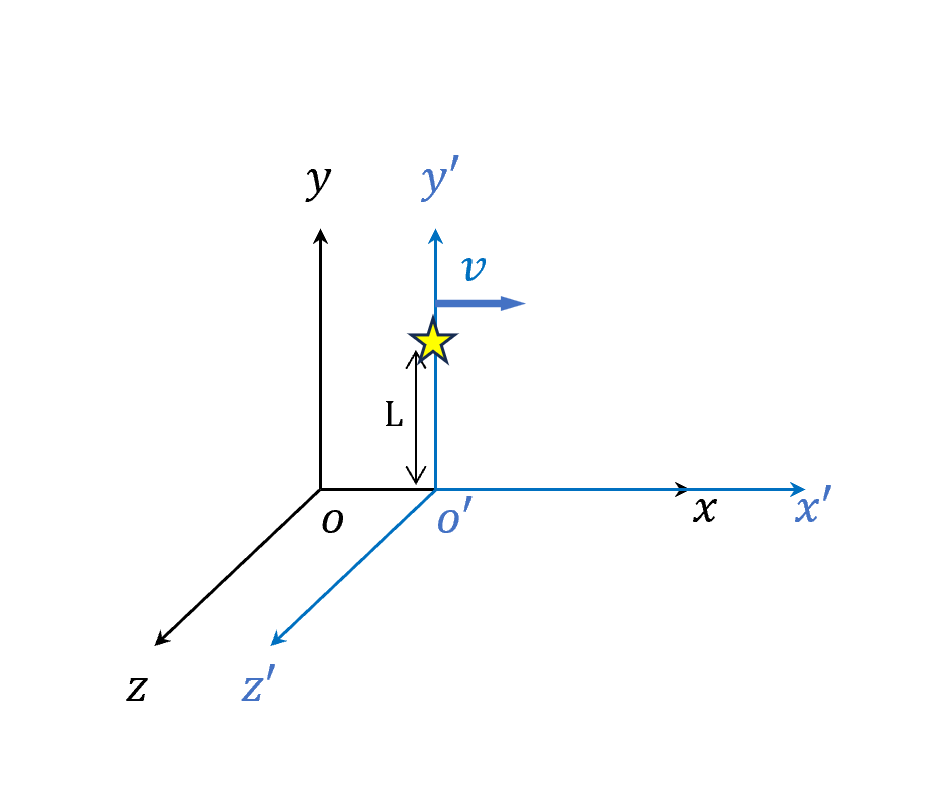
現在定義在移動坐標系的兩個的光線發射事件:
\[\begin{cases} (t_1', x_1', y_1') = (0, 0, L)\\ (t_2', x_2', y_2') = (\Delta t', 0, L)\\ \end{cases}\]在黑色座標系下,做勞倫茲轉換 (速度在x方向)
\[\begin{cases} ct_1=\gamma(ct_1'+\beta x_1')=0\\ x_1 = \gamma(x_1'+\beta c t_1') = 0\\ y_1 = L\\ ct_2=\gamma(ct_2'+\beta x_2')=\gamma c \Delta t'\\ x_2 =\gamma(x_2'+\beta c t_2')=\gamma \beta c \Delta t'\\ y_2 = L \end{cases}\]接收端時間差
黑色座標系下的接收端在$(x,y) = 0$,如圖
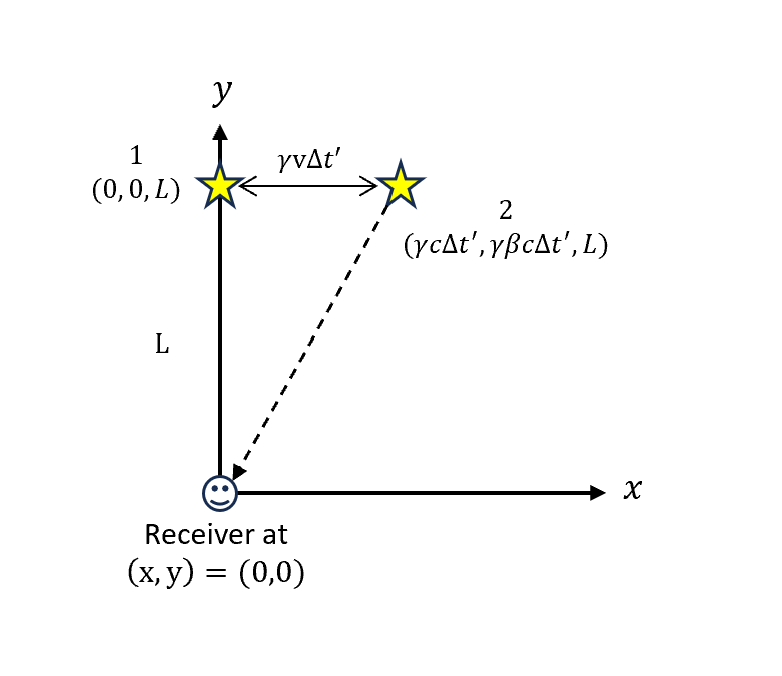
所以兩次收到的事件,收到的時間各自為
\[\begin{cases} T_1 = \frac{L}{c}\\ T_2 =\sqrt{\frac{L^2+(\gamma v\Delta t')^2}{c}}+\gamma\Delta t' \end{cases}\]假設
\[L\gg \gamma v\Delta t'\]得到兩個事件時間差
\[T_2-T_1\approx\gamma \Delta t'\]接收端頻率
換算頻率
\[\frac{1}{f_{observed}}=T_2-T_1=\gamma \Delta t'=\gamma\frac{1}{f_{emission}}\\ \Rightarrow f_{observed}=f_{emission}\times\frac{1}{\gamma}\]可以看到有$\gamma$在裡頭,這樣的都普勒效應是單純因為Time dilation造成的結果,跟波的壓縮拉長沒有關係。
