(2) Small Oscillation ─ Periodic Boundary Condition
求解N顆粒子的Normal Modes
現在來舉個簡單的粒子,假設一條彈簧,兩邊接牆壁,中間串N顆粒子,求解EOM。
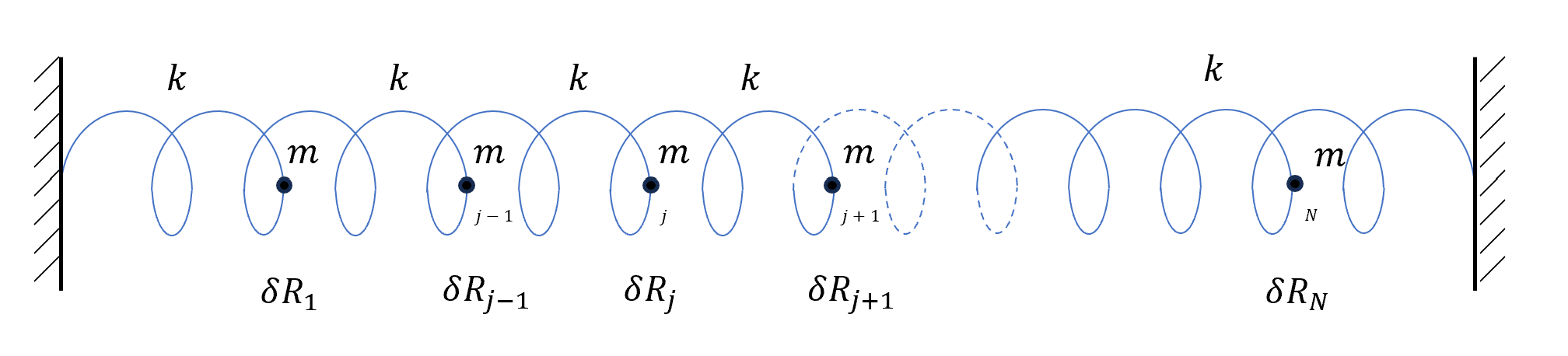
對於$j^{th}$粒子,EOM
\[m\frac{d^2\delta R_j}{dt^2} = -k(\delta R_j - \delta R_{j+1}) -k(\delta R_j - \delta R_{j-1})\\ = -2k \delta R_j + k(\delta R_j + \delta R_{j+1})\\ (j=1,2,\cdots,N)\]邊界條件BC為
\[\begin{cases} \delta R_0 = 0\\ \delta R_{N+1} = 0 \end{cases}\]根據上一節的討論,求該粒子的Normal Mode
\[-\omega^2 m \delta R_j = -2k \delta R_j + k(\delta R_{j-1} + \delta R_{j+1})\]方法一
我們試著直覺地一步一步拆解,先隨便猜一個$\omega$代進去。
(1) $j=1$
對$j=1$來說
\[-\omega^2 m \delta R_1 = -2k \delta R_1 + k(\underbrace{\delta R_0}_{0} + \delta R_2)\]可以看到我們可以用$\delta R_1$來表示$\delta R_2$。
(2) $j=2$
同理對$j=2$
\[-\omega^2 m \delta R_2 = -2k \delta R_2 + k(\delta R_1 + \delta R_3)\]因為$\delta R_2$可以用$\delta R_1$表示,那這裡待求的$\delta R_3$一樣可以用$\delta R_1$來替換。
(3) $j=N$
重複上述步驟一直求
\[\delta R_1, \delta R_2, \cdots, \delta R_N\]並且都用$\delta R_1$來替換(公式會超複雜)。
不過回來看一下最後一顆的公式,求$N^{th}$粒子時,會算$\delta R_{N+1}$
\[-\omega^2 m \delta R_N = -2k \delta R_N + k({\delta R_{N-1}} + \underbrace{\delta R_{N+1}}_{?})\](4) 邊界條件的問題?
我們從前面的邊界條件知道$\delta R_{N+1}$要等於0,但一開始我們是隨便猜$\omega$的數值,可能解到第N步發現$\delta R_{N+1}$不等於0,那就代表猜錯了,要再重新用別$\omega$!
需要猜到真正對的$\omega$,才能最後滿足邊界條件$\delta R_{N+1}=0$,這也是為什麼求 Normal Modes 頻率一定是特定值的關係。
從這裡可以更清楚地看到,完全符合我們以前所學的,像是多加了邊界條件之後,解會量子化的關係等等,因為這些邊界條件導致$\omega$一定是特定的數值,不能是任意的。
可是,那我們怎麼知道一開始到底要怎麼猜!?
所以這個方法一定是不可行!
方法二
我們換個進階的方法。
把原本的 3-terms recursion relation
\[-m\omega^2 \delta R_j = -2k \delta R_j + k(\delta R_{j-1} + \delta R_{j+1})\]改寫一下
\[\Rightarrow \left(\frac{-m\omega^2}{k}+2\right)\delta R_j - \delta R_{j-1} =\delta R_{j+1}\]再轉換成矩陣模式 2-term recursion relation
\[\Rightarrow \begin{pmatrix} \delta R_{j+1} \\ \delta R_j \end{pmatrix} = \begin{pmatrix} -\frac{m\omega^2}{k}+2 & -1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} \delta R_j \\ \delta R_{j-1} \end{pmatrix}\\ \Rightarrow \vec{W}_{j+1} = \hat{A} \vec{W}_j\]展開求到N+1項
\[\Rightarrow \vec{W}_{N+1} = \hat{A} \vec{W}_N = \hat{A}^2 \vec{W}_{N-1} = \cdots = \hat{A}^N \vec{W}_1\]這時重點就在於要求解
\[\hat{A}^N\]簡單一點就是去算對角化的矩陣 (2D eigen problem)
\[\begin{cases} \hat{A} \vec{\epsilon}_1 = \Lambda_1 \vec{\epsilon}_1\\ \hat{A} \vec{\epsilon}_2 = \Lambda_2 \vec{\epsilon}_2\\ \end{cases}\] \[\vec{\epsilon}_j\in\mathbb{R}^2\]並且寫下初始值
\[\vec{W}_1 \equiv l_1\vec{\epsilon}_1 + l_2\vec{\epsilon}_2\\ (l_1, l_2\text{ numerical value})\]合併一下
\[\begin{align} \Rightarrow \hat{A}^N \vec{W}_1 &= \Lambda_1^N l_1 \vec{\epsilon}_1 + \Lambda_2^N l_2 \vec{\epsilon}_2\\ &=\vec{W}_{N+1}\\ &\equiv\begin{pmatrix} \delta R_{N+1} \\ \delta R_N \end{pmatrix}\\ \end{align}\]邊界條件仍然是問題
看起來公式簡單多了,可是為了要符合邊界條件的$\delta R_{N+1}=0$,我們還是得去猜$\omega_1$,即便狂調整到對了,但一樣也只能解這次的問題。
如果下一個問題碰到$k$不一樣,或是邊界條件有點小變,或是中間有一顆粒子沒串,那整個就還是得重新猜重新解!
方法三:Periodic Boundary Condition
這時候我們從物理的自然現實出發,雖然自然頻率會和邊界條件有關係,但我們預期像是一塊晶體,一個金條,很長很大,假設有一億顆在裡面,那即便稍微改一點邊界條件,數學上的確自然頻率會變,但會覺得這些遠遠的變動改變不大,物理上對自然頻率不會改變太多。
想像上就是把剛剛一串的彈簧頭尾給接起來!稱為 Periodic Boundary Condition,如下圖
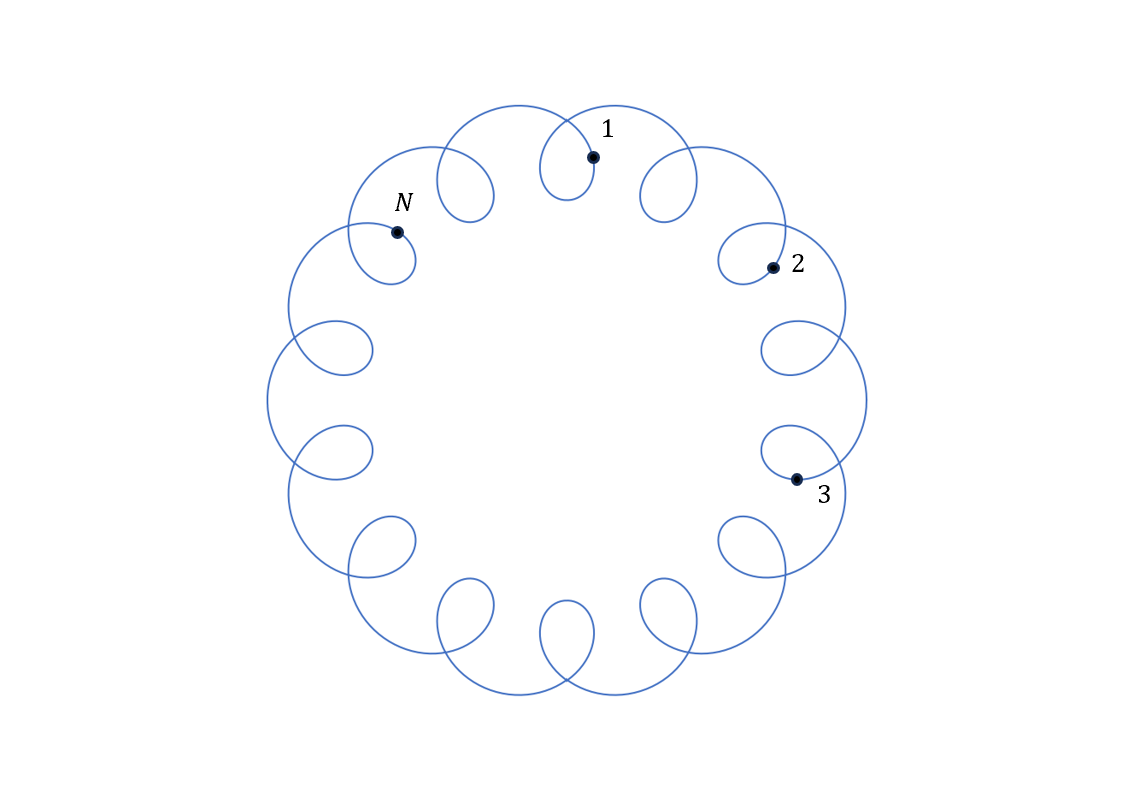
不過還是說明一下,其實也不是說物理上這樣做就是對的,這個「可連」的重點在於系統有對稱性(translational symmetry),整個系統移一點點還是一樣的symmetry,所以物理上相信真實的系統,因為粒子很多(N很大),所以邊邊改變一點,對中間的影響不大,算是一種犧牲Boundary Condition,但是解法就變得很簡單。
