(1) Small Oscillation ─ Normal Mode Justification
新的主題開始,來講Small Oscillation。
系統假設
假設我們現在有一些粒子在三維運動,大家質量不同,粒子間有交互作用,並且一起放在external potential field,然後來解運動方程EOM。
EOM
定
\[\vec{r_j}\equiv\text{ position of the }j^{th}\text{ particle of mass }{m_j}\\ V(\vec{r_1}, \cdots, \vec{r_N})\equiv\text{ potential energy}\]對於$j^{th}$的粒子,EOM為
\[m_j \frac{d^2\vec{r}_j}{dt^2} = -\frac{\partial V}{\partial \vec{r}_j}\]現定
\[\vec{R} = \begin{pmatrix} \vec{r}_1 \\ \vec{r}_2 \\ \vdots \\ \vec{r}_N \end{pmatrix}\]可以用矩陣表示全部的粒子
\[\hat{M} \frac{d^2\vec{R}}{dt^2} = -\frac{\partial V}{\partial \vec{R}}\]其中質量的矩陣就會是對角化矩陣,且因為三維,所以一個$m_j$會有三個
\[\begin{pmatrix} m_1 & & & & & & \\ & m_1 & & & & & \\ & & m_1 & & & & \\ & & & m_2 & & & \\ & & & & m_2 & & \\ & & & & & m_2 & \\ & & & & & & \ddots \\ \end{pmatrix}\]Equilibrium Point
假設這個系統有一個 stationary solution $\vec{R}_0$,是 fixed point,視為 equilibrim solution,用數學公式說就是
\[\left.\frac{\partial V}{\partial \vec{R}}\right|_{\vec{R}_0} = 0\]Perturbation
回到我們前面的 $\vec{R}$,與平衡點$\vec{R}_0$ 差微量 $\delta \vec{R}$。
然後看這個變化量的EOM,一樣近似到一階。
(做法一樣可參考軌跡第一節,只是軌跡主要是要看shape,現在則是要看擾動量隨時間的演化)
\[\hat{M} \frac{d^2\vec{R}}{dt^2} = -\frac{\partial V}{\partial \vec{R}}\quad -(1)\\ \hat{M} \frac{d^2\vec{R}_0}{dt^2} = -\frac{\partial V}{\partial \vec{R}_0}\quad -(2)\\ (1)-(2)\Rightarrow\hat{M} \frac{d^2\delta \vec{R}}{dt^2} = -\frac{\partial^2 V}{\partial \vec{R}_0 \partial \vec{R}_0} \cdot \delta \vec{R}\text{ (symmetric matrix)}\]$$ \begin{align} F(\vec{R})&\equiv-\frac{\partial V}{\partial \vec{R}}\\ &=F(\vec{R}_0+\delta \vec{R})\\ &=F(\vec{R}_0)+F'(\vec{R}_0)\delta\vec{R}+\frac{1}{2}F''(\vec{R}_0)(\delta\vec{R})^2+\cdots\\ \Rightarrow F(\vec{R})-F(\vec{R}_0)&\approx F'(\vec{R}_0)\delta\vec{R}\\ &=-\frac{\partial ^2 V}{\partial \vec{R}_0\partial \vec{R}_0}\delta\vec{R} \end{align} $$
Rewrite the EOM (Hooke’s Law)
因為位能展開
\[V(\vec{R}) = V(\vec{R}_0) + \frac{\partial V}{\partial \vec{R}_0} \cdot \delta \vec{R} + \frac{1}{2} \delta \vec{R} \cdot \frac{\partial^2 V}{\partial \vec{R}_0 \partial \vec{R}_0} \cdot \delta \vec{R} + \cdots\]其中第二項因為$\vec{R}_0$ 是 equilibrium solution,所以為零。
那麼看第三項,就會假設$\frac{\partial^2 V}{\partial \vec{R}_0 \partial \vec{R}_0}$ 一定要是 positive definite matrix。
數學上來說就是
\[\delta \vec{R} \cdot \frac{\partial^2 V}{\partial \vec{R}_0 \partial \vec{R}_0} \cdot \delta \vec{R} \geq 0 \\ \text{and it vanishes only if } \delta \vec{R} = \vec{0}.\]物理上的原因是,這個位能的二階一定要是開口朝上,才能表示$\vec{R}_0$ 會是穩定的平衡點,是最小值,往旁邊移動一點點位能都比較大。不然如果還有更小的位能點,粒子就會繼續傾向跑到那邊,不會回來了。
所以我們額外定
\[\hat{c}\equiv\frac{\partial^2 V}{\partial \vec{R}_0^2}\]重寫EOM
\[\hat{M} \frac{d^2\delta \vec{R}}{dt^2} = -\hat{c} \cdot \delta \vec{R}\]看起來就是 Hooke’s law!對應 $\hat{c}$ 是 generalization of spring constant,所以可以看到要$>0$,才會振盪回來。
一般解法
到這裡我們一般解
\[\hat{M} \frac{d^2\delta \vec{R}}{dt^2} = -\hat{c} \cdot \delta \vec{R}\]通常就直接假設
\[\delta\vec{R} \equiv e^{-i\omega t} \delta\vec{R}_0\]然後帶進去
\[-\omega^2 \hat{M} \delta \vec{R}_0 = -\hat{c}(\delta\vec{R}_0)\\ (\omega^2\hat{M}-\hat{c})\cdot(\delta\vec{R}_0) = \vec{0}\\ \Rightarrow \det(\omega^2\hat{M}-\hat{c}) = 0\]解完就可找到頻率
\[\omega_{j}\]和對應的
\[\delta\vec{R}_0\]可是!這個假設的基礎是什麼?為什麼$\omega$一定會是正的實數呢?
下面我們來做驗證。
從別的角度驗證
重寫EOM
\[\begin{align} \hat{M}^{\frac{1}{2}} \frac{d^2(\hat{M}^{\frac{1}{2}} \delta \vec{R})}{dt^2} &= -\hat{c} \hat{M}^{-\frac{1}{2}} (\hat{M}^{\frac{1}{2}} \delta \vec{R})\\ \Rightarrow \frac{d^2(\hat{M}^{\frac{1}{2}} \delta \vec{R})}{dt^2} &= -(\hat{M}^{-\frac{1}{2}} \hat{c} \hat{M}^{-\frac{1}{2}}) (\hat{M}^{\frac{1}{2}} \delta \vec{R})\\ \Rightarrow \frac{d^2 \vec{\xi}}{dt^2} &\equiv -\hat{B} \vec{\xi} \end{align}\]因為$\hat{c}$維持symmetric positive definite matrix,然後前後只是乘上對角化的質量矩陣,所以$\hat{B}$也還是positive definite symmetric matrix。
可以檢查一下
\[\hat{B}^t = (\hat{M}^{-\frac{1}{2}} \hat{c} \hat{M}^{-\frac{1}{2}})^t = (\hat{M}^{-\frac{1}{2}})^t (\hat{c})^t (M^{-\frac{1}{2}})^t = (\hat{M}^{-\frac{1}{2}}) (\hat{c}) (\hat{M}^{-\frac{1}{2}}) =\hat{B}\]竟然$\hat{B}$是positive definite,我們可以找一組正交歸一的基底(orthonormal basis)
\[\hat{e}_1, \hat{e}_2 \cdots\]使得
\[\hat{B} \hat{e}_j = \lambda_j \hat{e}_j\\ (\lambda_j > 0,\because \hat{B}\text{ is positive definite})\]那就可以額外定義一個平方來保證正數
\[\hat{B} \hat{e}_j\equiv \omega_j^2 \hat{e}_j \quad - (1)\]然後$\xi$ 是這組基底的線性組合
\[\vec{\xi}(t) = \sum_j a_j(t) \hat{e}_j\]代進原本EOM
\[\begin{align} \frac{d^2 \vec{\xi}}{dt^2} &= -\hat{B} \vec{\xi}\\ \Rightarrow \sum_j \frac{d^2a_j(t)}{dt^2} \hat{e}_j &= -\hat{B} \vec{\xi}\\ &= -\hat{B} (\sum_j a_j(t) \hat{e}_j) \\ &= -\sum_j a_j(t) \hat{B}\hat{e}_j\\ &= \sum_j (-a_j) \omega_j^2 \hat{e}_j \end{align}\]得
\[\Rightarrow \frac{d^2a_j}{dt^2} = -\omega_j^2 a_j\]!!可以看到每一個$a_j$就會是隨著時間在振盪(oscillates sinusoidally)的解了!
所以我們可以繼續寫,把$a_j$拆成振盪的線性組合解
\[\vec{\xi} = \sum_j a_j(t)\hat{e}_j = \sum_j (b_j e^{-i\omega_j t} + b_j' e^{i\omega_j t}) \hat{e}_j=\hat{M}^{\frac{1}{2}}(\delta\vec{R})\\ (b_j, b_j'\text{ is const})\] \[\Rightarrow \delta\vec{R} = \sum_j (b_j e^{-i\omega_j t} + b_j' e^{i\omega_j t})\hat{M}^{-\frac{1}{2}}\hat{e}_j\quad - (2)\]最後回到改寫後的EOM
\[\frac{d^2 \vec{\xi}}{dt^2} \equiv -\hat{B} \vec{\xi}\\ -\omega_j^2 \hat{e}_j = -\hat{M}^{-\frac{1}{2}} \hat{c} M^{-\frac{1}{2}} \hat{e}_j\]等於是我們可以簡單地把$\frac{d^2}{dt^2}$替換成$-\omega_j^2$,所以在原始的EOM
\[\hat{M} \frac{d^2\delta \vec{R}}{dt^2}=-\hat{c}(\delta\vec{R})\\ \Rightarrow\hat{M} -\omega_j^2 \delta \vec{R}=-\hat{c}(\delta\vec{R})\]解下去的$\omega_j$就是系統normal modes的頻率,每一個eigen vector$\delta\vec{R}$就是normal modes,可以很好地把這個複雜的系統decompose to tiny problem。
所以勒?
說明到這裡,看起來都是已知的訊息。
但是從(1)和(2)式可以看出來我們一般解的假設中
- $\omega$是正數起自於(1)式,代表原本要滿足平衡點是在最低點而有的positive definte matrix。
- $\delta\vec{R}$則來自於(2)式的推導。
最後上一張圖,總結一下這裡一直提的positive-definite代表什麼。
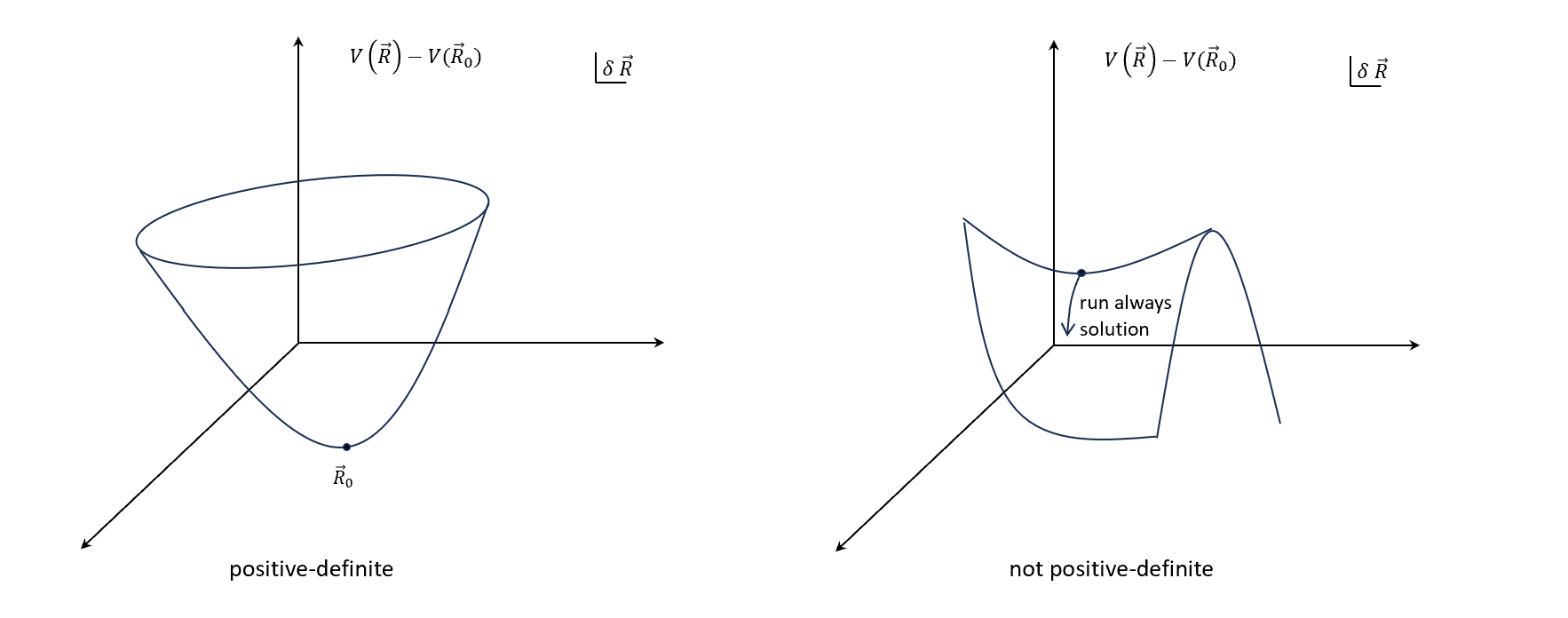
Normal Modes 的精神
後續章節會舉更多的例子來求 normal modes,可是這邊要先提的一點是,當我們在說要解一個系統的 normal modes 時,並不是在說這個系統的運動都是purely sinusoidal in time,實際上的運動一定是相當複雜(例如串N顆粒子的彈簧運動)。
進一步地是,sinusoidal motion是建立在特定狀態的起始位置,就是把每一顆粒子都先放在特定的位置(某個eigen vetor normal mode),開始運動的時候才可以單純用某個sinusoidal $\omega$ 的頻率來運動。
如果起始條件是亂放亂拉的,那麼放手後就會亂振,運動就很複雜了!
既然如此,normal modes 需要綁定特定的狀態,為什麼物理學上還花這麼多的功夫在研究這件事情?那是因為,不論一般情況下運動多複雜,最 general 的運動永遠都可以表示為這些 normal modes 的線性疊加!
The most general motion of the system can always be expressed as certain linear combinations of the normal modes.
(這裡可以順帶一提,線性代數本來就告訴我們解的eigen vetors form a complete bases)
所以從數學上來看就是,若
\[\delta \vec{R}^{(1)}, \delta \vec{R}^{(2)}, \cdots, \delta \vec{R}^{(N)}\]是 N 個 normal modes,
(譬如說有2顆粒仔的彈簧$\delta \vec{R}^{(1)}$ 就是→←、$\delta \vec{R}^{(2)}$就是 →→)
那麼某個時間點的運動可以表示成
\[\delta \vec{R}(t=0)\equiv \sum^N_{j=1}C_j\delta\vec{R_0}^{j}\\ (C_j: \text{determined by the initial condition})\]再加入時間頻率項,因為每個normal modes都是purely sinusoidal oscillation
\[\delta\vec{R}(t)\equiv \sum^N_{j=1}C_j\delta\vec{R_0}^{j}e^{-i\omega_j t}\]就能很方便的表示出一般運動狀態了!
