(3) Small Oscillation ─ Example: Linear Train
現在我們就結合前一節的方法二和方法三繼續解下去。
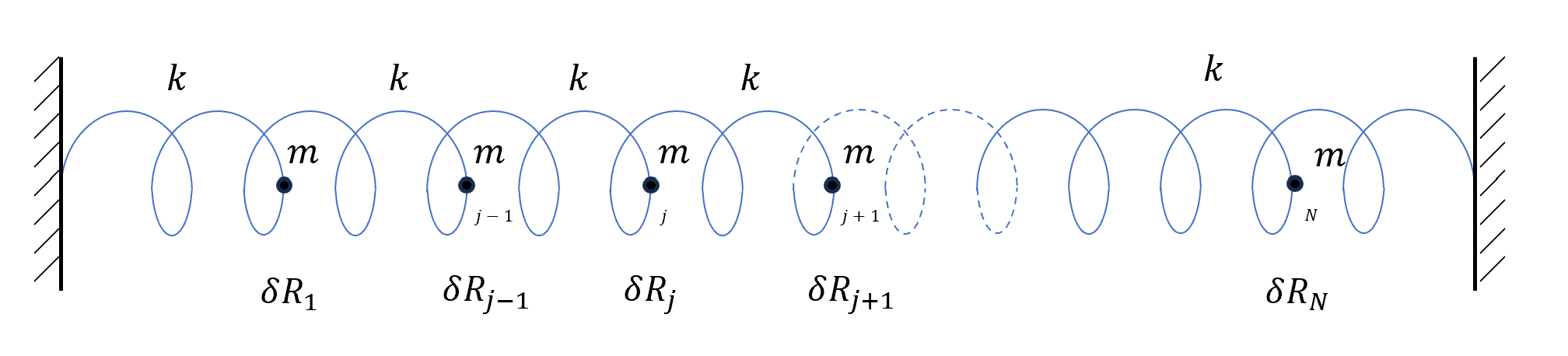
Translational Symmetry Operator
前面說到,用到 periodic boundary condition 隱含著 translation symmetry,所以如果
\[\begin{pmatrix} \delta R_{1} \\ \delta R_2 \\ \delta R_3 \\ \vdots \\ \delta R_N \end{pmatrix}\]是解答,那麼我們定一個translational symmetry operator
\[\hat{P}\]使得
\[\hat{P}(\delta \vec{R})\equiv \begin{pmatrix} \delta R_2 \\ \delta R_3 \\ \vdots \\ \delta R_N \\ \delta R_{1} \end{pmatrix}\]也會是解答。
如果我們重複做N次,就會回到原本自己,所以
\[\hat{P}^N=\hat{\mathbb{1}}\]Eigenvalue
若
\[\hat{P}^N=\hat{\mathbb{1}}\]要求其的Eigenvalue $\lambda$,則可知
\[\lambda^N = 1\]複數解可得(這裡簡單點處理N是偶數的情況)
\[\lambda_l = e^{i\frac{2\pi l }{N}},\quad l=-\frac{N}{2}, -\frac{N}{2}+1, ..., \frac{N}{2}-1, \frac{N}{2}\\ \left((e^{i\theta})^N=1, \quad \theta=\frac{2\pi}{N}\cdot l\right)\]Eigenvector
線性代數知道,若兩個operator commute,則有相同的eigen vector。
因此這裡因為$[\hat{P}, \hat{c}]=0$,所以前一節算的normal modes就是$\hat{P}$的 eigen vector。
\[\hat{P}\begin{pmatrix} \delta R_{1} \\ \delta R_2 \\ \delta R_3 \\ \vdots \\ \delta R_N \end{pmatrix} \equiv\begin{pmatrix} \delta R_2 \\ \delta R_3 \\ \vdots \\ \delta R_N \\\delta R_{1} \end{pmatrix} =e^{i\frac{2\pi}{N}l}\begin{pmatrix} \delta R_{1} \\ \delta R_2 \\ \delta R_3 \\ \vdots \\ \delta R_N \end{pmatrix}\]展開條列一下
\[\begin{align} \delta R_2 &= e^{i\frac{2\pi}{N}l}\delta R_1\\ \delta R_3 &= e^{i\frac{2\pi}{N}l}\delta R_2 = e^{(i\frac{2\pi}{N}l)\times 2}\delta R_1 \\ &\vdots\\ \delta R_j &= e^{(i\frac{2\pi}{N}l)(j-1)}\delta R_1\equiv e^{(i\frac{2\pi}{N}l)(j)}\delta R_0\\ &(j\text{: index of the }j^{th}\text{ particle}) \end{align}\]波的形式
前面我們都指定是哪一顆粒子,現在更general一點,直接定位置
\[x\equiv j\cdot a\]其中$a$是每一個粒子之間的距離(lattice spacing)。
所以
\[\delta R_j = e^{(i\frac{2\pi}{N}l)(j)}\delta R_0\\ \Rightarrow \delta R_x = e^{i\frac{2\pi l}{Na}ja}\delta R_0\equiv e^{ik_l x}\delta R_0\\ k_l\equiv \frac{2\pi}{Na}l\\ (\text{a sort of wave number indexed by }l)\]這裡解釋一下,當初我們在解eigenvalue和eigenvector的時候,是用$l$來代表,所以現在定義的$k_l$就是把該組eigenvector(eigenvalue)轉成波的形式,$k_l$就是wave number。
而每組eigenvetor,就是這串上所有粒子的displacement($\delta R_x)$,所以簡單來說,每一組eigenvector展現的粒子displacement(normal modes),都對應到一個波數為$k_l$的波。
反過來說,假設有一百顆粒子,就有一百個normal modes,每一個normal mode的wave number對應的波動,就是這一百個粒子在當下的displacement。
因此我們可以進一步去寫
\[\delta R_x\propto e^{ik_l x}e^{-i\omega_l t}\]這裡的$\omega_l$也用$l$當作label,因為代表normal frequency也是對照到每一組eigenvector。
那麼這個式子整合起來就是個propagating wave pattern(往左往右)的plane wave了!
短波長波
$l$竟然決定了是哪一個normal modes,那我們來看極端的情況。
因為
\[\delta R_j = e^{(i\frac{2\pi l}{N})}\delta R_{j-1}\]若 $l=N/2$,$e^{i\pi}=-1$,代表每個相鄰的粒子都是180度的out of phase,排列就很像是↑↓↑↓,直接顛倒運動,波長是最短的。
相反若 $l$ 很小,那鄰居就都差一點,變化很緩慢,看起來就是比較平緩的波,就會是長波。
求解EOM
講了一堆,直接回來EOM求解。記得一開始(這裡以防跟波數混淆,彈性係數用C取代)
\[m\frac{d^2\delta R_j}{dt^2} = -C(\delta R_j - \delta R_{j+1}) -C(\delta R_j - \delta R_{j-1})\\ \Rightarrow -m\omega^2\delta R_j = -C(\delta R_j - \delta R_{j+1}) -C(\delta R_j - \delta R_{j-1})\]又
\[\because \delta R_j \propto e^{i\frac{2\pi l}{N}\cdot j}\]我們再把$\delta R_j \equiv 1$簡單化代進去
\[\begin{align} \Rightarrow -m\omega^2_l\cdot 1 &= -2C\cdot 1 + C e^{-i\frac{2\pi l}{N}(-1)}+Ce^{i\frac{2\pi l}{N}}(1)\\ -m\omega^2_l\cdot 1 &= -2C\cdot 1 + 2C \cos{\frac{2\pi l}{N}} \end{align}\]移項
\[\begin{align} \omega_l^2&=\frac{2C}{m}\left(1-\cos{\frac{2\pi l}{N}}\right)=\frac{2C}{m}2\bigg|\sin{\frac{2\pi l}{N}}\bigg|\\ \Rightarrow \omega_l&=\sqrt{\frac{C}{m}}2\bigg|\sin{\frac{\pi l}{N}}\bigg|=\sqrt{\frac{C}{m}}2 \sin{\frac{ka}{2}}\\ \end{align}\]可以看到
\[\omega=\omega(k)\]$\omega$和$k$非線性關係,是dipersive wave!
Dispersive Wave
不過我們可以畫個圖來分析一下
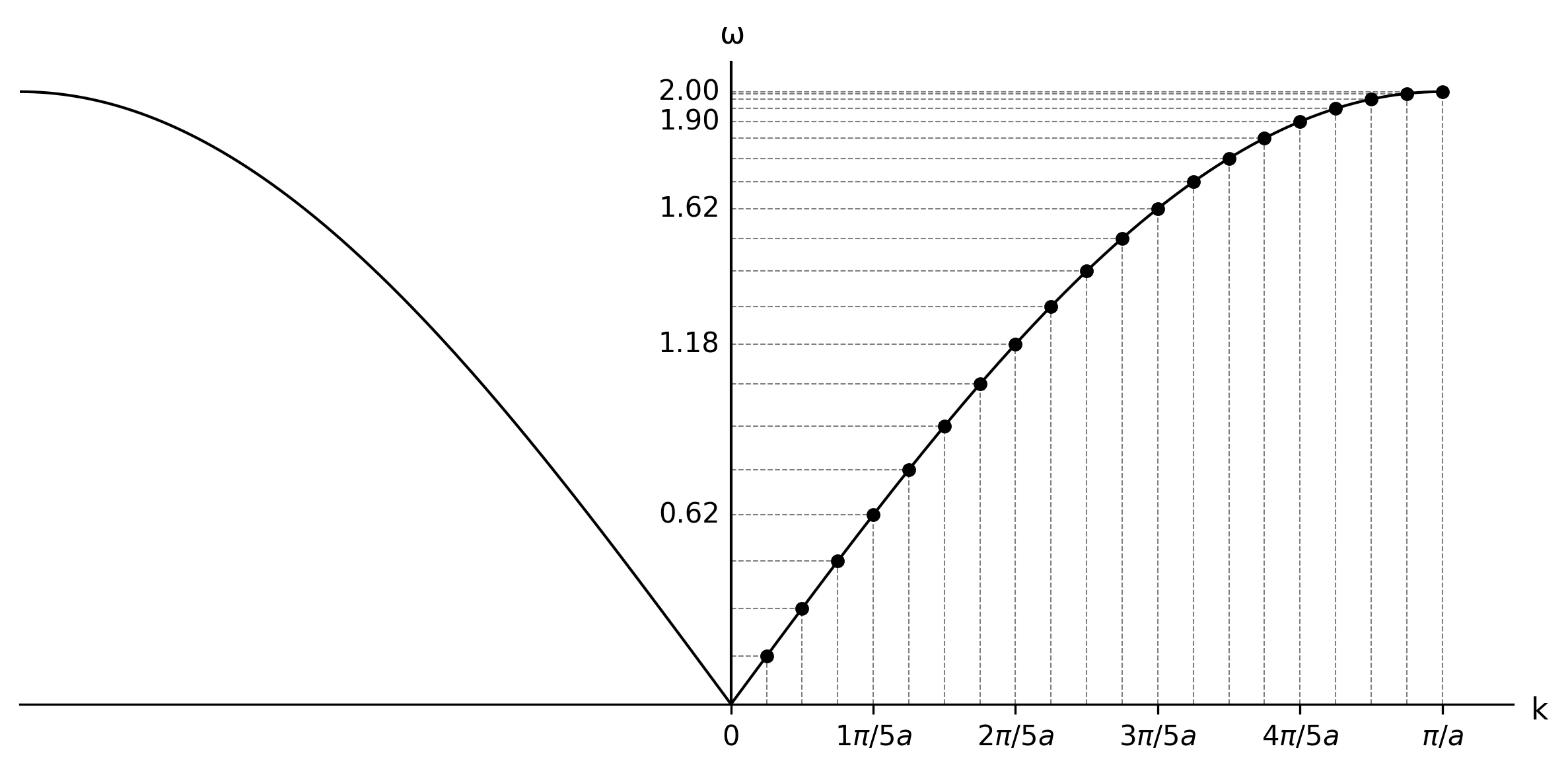
- 若$k$很小:可以視為線性沒有dipersive,討論的波長比$a$大很多
- $k$越大:dispersion就看得出來,$\omega$對應的點就不是等間隔了(有疏密的變化)!
The distribution of the normal modes is uniform in $k$, but not in $\omega$!
