Cjue25

Good things take time

現在晶體有內部結構(internal structure)，就像食鹽一樣，有Na和Cl排成特定結構，彼此都會影響。

我們把這個問題簡化成以下問題，大小粒子之間彈性係數是$K$ (internal)，lattice之間彈性係數是$C$。

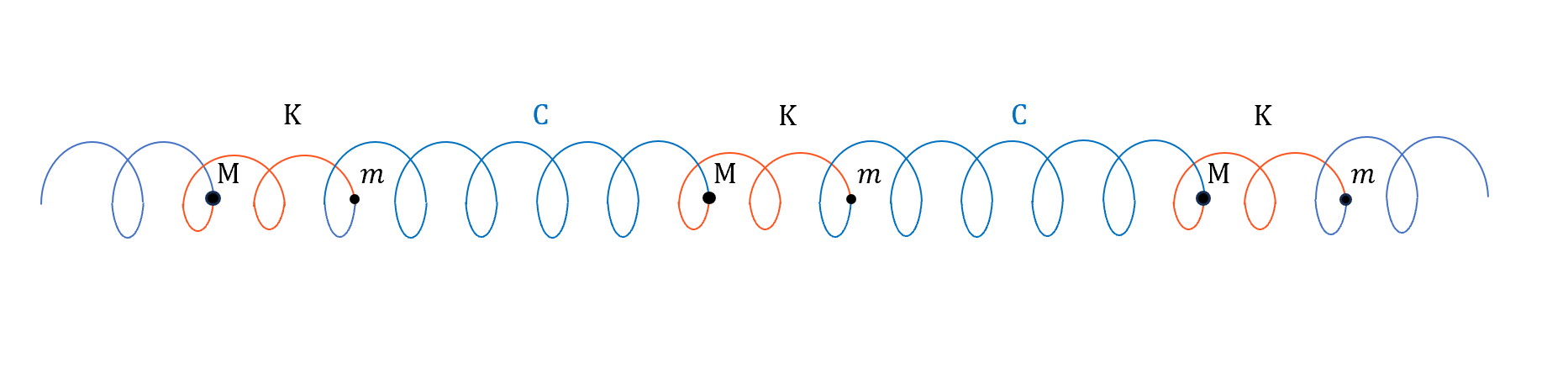
求解EOM

定Displacement

\[\begin{cases} M: \xi_j\\ m: \eta_j \end{cases}\]

馬上來列出EOM

\[\begin{cases} M \frac{d^2\xi_j}{dt^2} = -C(\xi_j - \eta_{j-1}) - K(\xi_j - \eta_j) \\ m \frac{d^2\eta_j}{dt^2} = -K(\eta_j - \xi_j) - C(\eta_j - \xi_{j+1}) \end{cases}\]

用前面的方法寫下Normal modes

\[\xi_j \equiv \xi_0 e^{i\frac{2\pi}{N}lj} \\ \eta_j \equiv \eta_0 e^{i\frac{2\pi}{N}lj}\\ \frac{d^2}{dt^2} \to -\omega_l^2\]

代進EOM

\[\begin{cases} -M\omega_l^2\xi_0 = -(C+K)\xi_0 + C\eta_0 e^{-i\frac{2\pi}{N}l} + K\eta_0 \\ -m\omega_l^2\eta_0 = -(C+K)\eta_0 + K\xi_0 + C\xi_0 e^{i\frac{2\pi}{N}l} \end{cases}\]

轉化成矩陣的形式

\[\begin{pmatrix} M\omega_l^2 - (C+K) & K + Ce^{-i\frac{2\pi}{N}l} \\ K + Ce^{i\frac{2\pi}{N}l} & m\omega_l^2 - (C+K) \end{pmatrix} \begin{pmatrix} \xi_0 \\ \eta_0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}\]

要求得nontrivial solution for $(\xi_0, \eta_0)$，所以

\[\det(\text{matrix})=0\]

來求

\[(M\omega_l^2 - (C+K))(m\omega_l^2 - (C+K)) - (K + Ce^{-i\frac{2\pi}{N}l})(K + Ce^{i\frac{2\pi}{N}l}) = 0\\ Mm\omega_l^4 - (C+K)(m+M)\omega_l^2 + (C+K)^2 - \left(K^2 + C^2 + KC2\cos\frac{2\pi}{N}l\right) = 0\\ Mm\omega_l^4 - (C+K)(m+M)\omega_l^2 + 2CK\left(1 - \cos\frac{2\pi}{N}l\right) = 0\\ Mm\omega_l^4 - (C+K)(m+M)\omega_l^2 + 4CK\sin^2\frac{\pi}{N}l = 0\\ \Rightarrow\omega_l^2 = \frac{(C+K)(M+m) \pm \sqrt{(C+K)^2(M+m)^2 - 16MmCK\sin^2(\frac{\pi}{N}l)}}{2Mm}\]

可以看到$\omega_l^2$會有兩個解。

Optical Branch Solution：$\omega_l^{2(+)}$

我們假設一個limiting case $K \gg C$，那麼根號中

\[\sqrt{\cdots} \approx (C+K)(M+m)\left(1 - \frac{1}{2} \frac{16MmCK\sin^2\frac{\pi l}{N}}{(C+K)^2(M+m)^2}\right)\]

若 Correct to 1st order in C

\[\omega_l^{2(+)} = \frac{2(C+K)(M+m) - \frac{8MmCK\sin^2\frac{\pi l}{N}}{(C+K)(M+m)}}{2Mm}\\ \approx \frac{(C+K)(M+m)}{Mm} - \frac{4C\sin^2\frac{\pi l}{N}}{M+m}\\ \left(\because\frac{CK}{C+K}\approx\frac{CK}{K}\approx C\right)\]

再進一步看 Correct to 0th order of C

\[\omega_l^{2(+)} \approx K\underbrace{\frac{M+m}{Mm}}_{\text{reduced mass}}\]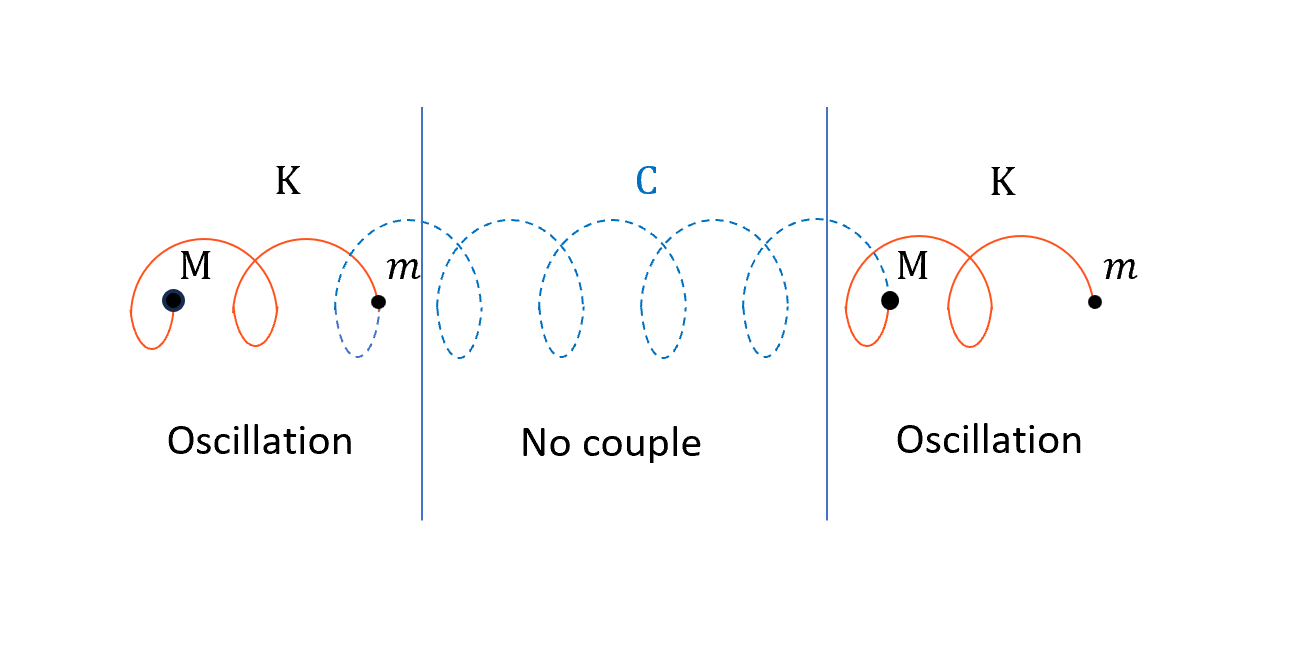

把 C 扔掉的話，剩下 K，相當於分子之間沒有 coupling，只有單一晶格間自己內部的原子振動(能組成一個unit一定有很強的束縛)。

這很像以前我們學過的兩個木塊中綁彈簧，可以用質心和reduced mass來表示最後單一系統的normal freqency($\omega$)。(參考)

而若取到 first order，C回來，才代表分子間的 weak coupling。

Acoustic Branch Solution：$\omega_l^{2(-)}$

同理推導可得

\[\omega_l^{2(-)} = \frac{4C\sin^2\frac{\pi l}{N}}{M+m}\]

因沒有 K，可以把 M+m 視為一坨單位，很像前一節例子中的單一particle，所以只剩下 C 連結在一起。

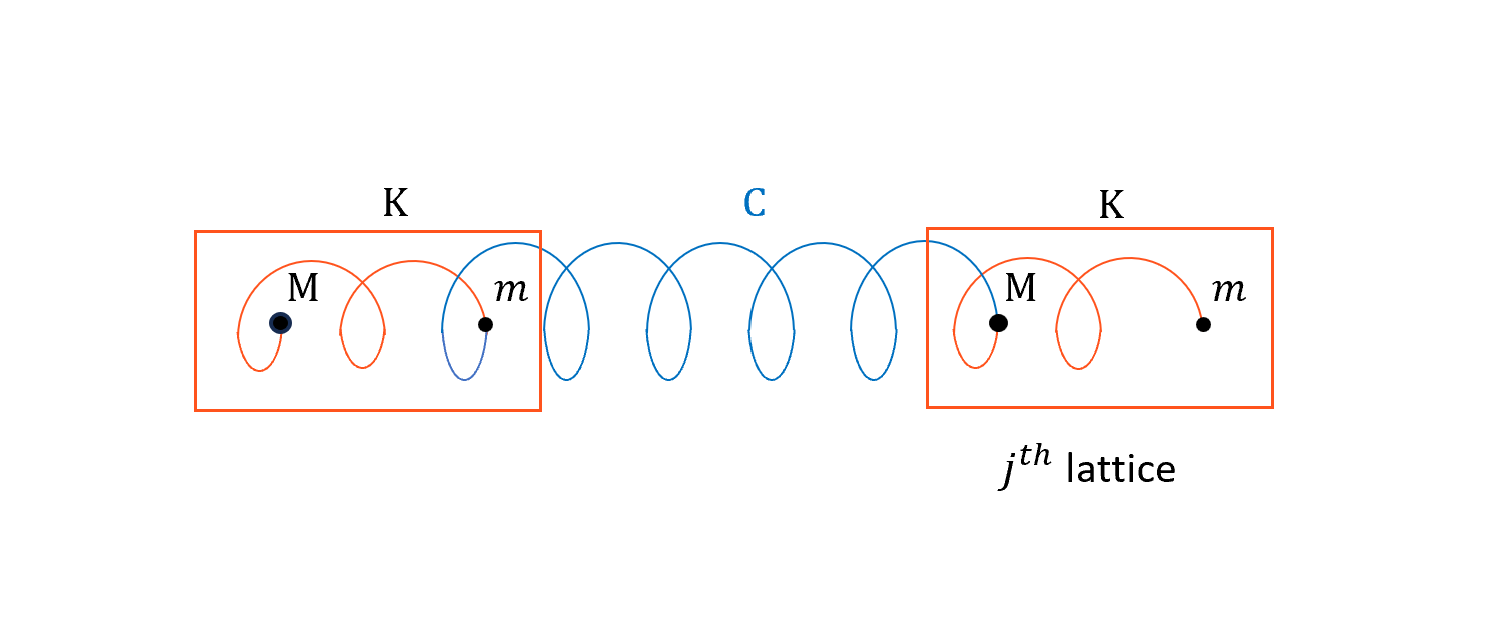
比較一下

\[\begin{cases} \omega_l=\sqrt{\frac{C}{m}}2\sin\frac{\pi l}{N}\quad\text{from previous chapter}\\ \omega_l^{2(-)} = \frac{4C\sin^2\frac{\pi l}{N}}{M+m} \end{cases}\]

現在整體變成是simpler linear chain with mass $(M+m)$，如果一樣採用長波來解(k很小)，就會是 non-dispersive wave，

Normal Modes

統整一下，現在會有兩個解，在$K\gg C$的情況下，取最低階的解答是

  • Optical：$\omega_l^{2(+)} \approx K\frac{M+m}{Mm}$
  • Acoustic：$\omega_l^{2(-)} = \frac{4C\sin^2\frac{\pi l}{N}}{M+m}$

畫個圖，可以再次看到 Optical 的頻率較高，Acoustic 的則是像前一節的 Linear Train Example。

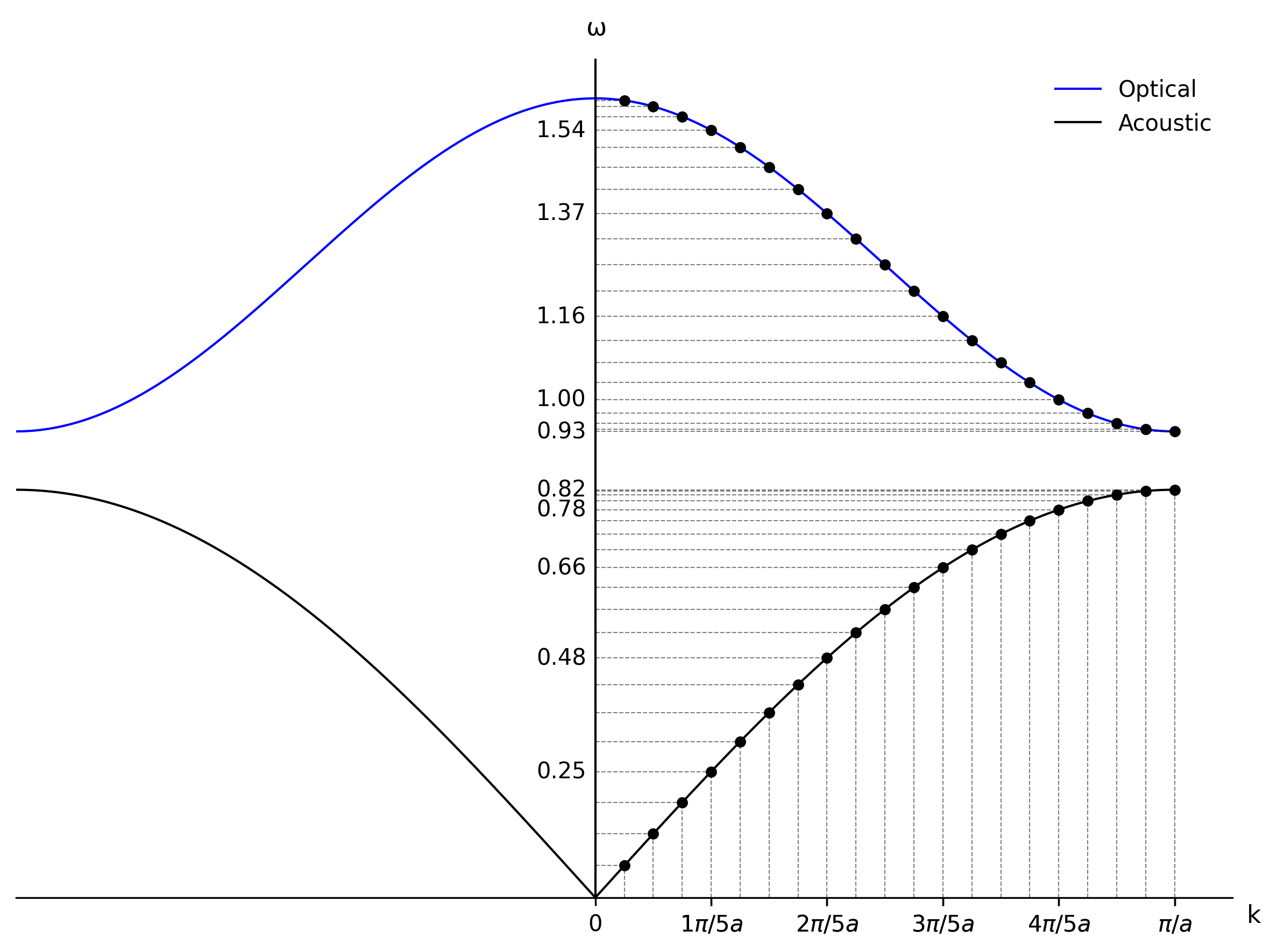
現在我們進一步看兩者的 Eigenvectors。

回顧 EOM

\[\begin{pmatrix} M\omega_l^2 - (C+K) & K + Ce^{-i\frac{2\pi}{N}l} \\ K + Ce^{i\frac{2\pi}{N}l} & m\omega_l^2 - (C+K) \end{pmatrix} \begin{pmatrix} \xi_0 \\ \eta_0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}\]

各自把$\omega^2$代進去解，一樣都只取最低階的accuracy，最後會得

Optical：

\[M\xi_0 + m\eta_0 = 0\]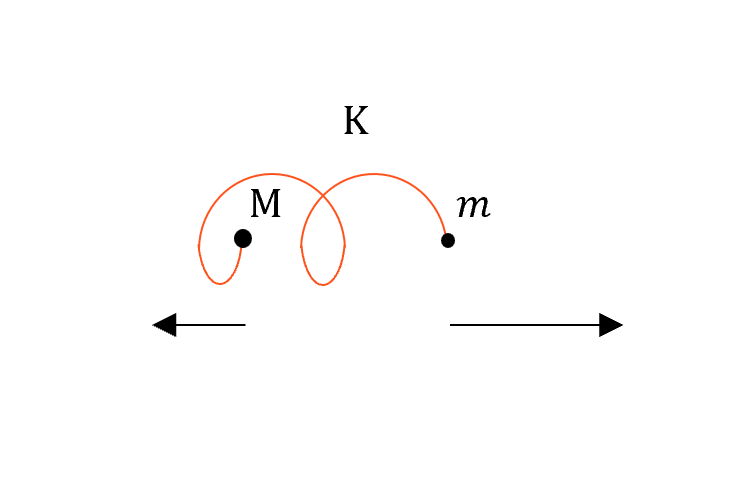

代表分子內部的振動，兩個粒子方向相反，但因為跟其他的分子無關，所以反應出質心固定($M\xi_0 + m\eta_0=0$)。

Acoustic：

\[\xi_0 = \eta_0\]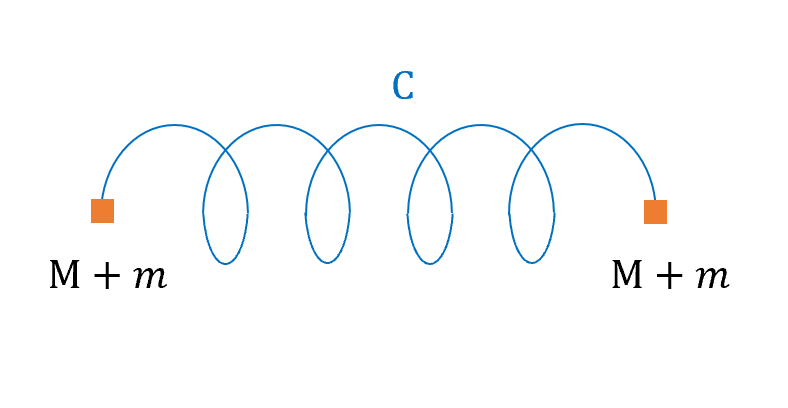

代表單一分子視為一個單位，分子內兩個粒子一起動，整體就像是前一節在解的 Linear Train Example。

實際應用

當然實際情況是所有各式各樣的狀態coupling在一起，所以在真實應用中我們就是去敲一下，然後把測量值拿去做傅立葉的頻譜分析，看裡面的 frequency component、dispersion relation、KCMm等等，就能進一步得知內部結構長什麼樣子。

You may also enjoy