(5) Small Oscillation ─ Example: Reflection Symmetry
前面在解 Linear Train 的時候,是用 Translation Symmetry 來解。
可以看到其實要解normal modes的系統通常都滿複雜,而且也有很多顆粒子,如果利用對稱性質就會好解很多。
所以現在我們繼續來看另外一個例子,用的是 Reflection Symmetry。
Reflection Symmetry Operator
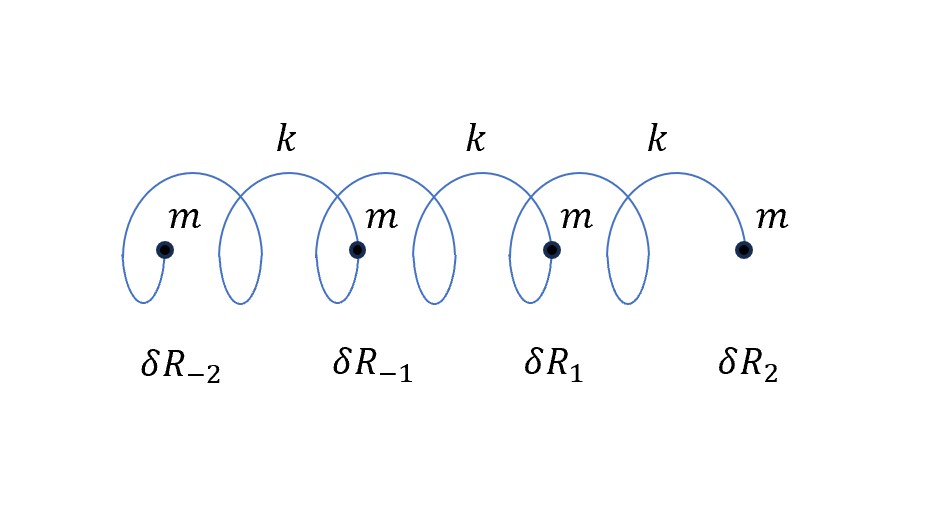
假設現在有四顆粒子,定義為
\[\psi= \begin{pmatrix} \delta R_2\\\delta R_1\\\delta R_{-1}\\\delta R_{-2} \end{pmatrix}\]定 reflection symmetry operator
\[\hat{P}(\psi)\equiv \begin{pmatrix} \delta R_{-2}\\\delta R_{-1}\\\delta R_{1}\\\delta R_{2} \end{pmatrix}\]Eigenvalue
因為
\[\hat{P}^2=\hat{\mathbb{1}}\]所以eigenvalue of $\hat{P} = \pm 1$
Eigenvector
對應有兩個eigenvector
- eigenvalue = 1 & eigenvetor $\psi_+$
- eigenvalue = -1 & eigenvetor $\psi_-$
EOM
現在雖然有四顆,但我們看右邊兩顆就好,左邊兩顆是一樣的道理
Particle 1
\[m\frac{d^2 \delta R_1}{dt^2} = -C(\delta R_1 - \delta R_2)-C(\delta R_1-\delta R_{-1})\]Particle 2
\[m\frac{d^2 \delta R_2}{dt^2} = -C(\delta R_2 - \delta R_1)\]Solution
$\psi_+$
對於$\psi_+$來說,因為symmetry
\[\delta R_{-1} = \delta R_{1}\]所以 EOM
\[\begin{cases} -m\omega^2 \delta R_1 = -C(\delta R_1 - \delta R_2)\\ -m\omega^2 \delta R_2 = -C(\delta R_2 - \delta R_1) \end{cases}\]用 matrix 來解
\[\begin{pmatrix} -C + m\omega^2 & C \\ C & -C + m\omega^2 \end{pmatrix} \begin{pmatrix} \delta R_2 \\ \delta R_1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}\] \[\Rightarrow m^2\omega^4-2mC\omega^2=0\]得到兩個解答
\[\omega^2=\frac{2mC\pm\sqrt{4m^2C^2}}{2m^2}\\ \omega^2 = 0, \frac{2C}{m}\]代回去求normal mode
- $\omega^2 = 0$
- $\omega^2 = \frac{2C}{m}$
可以看到 $\psi_{+}^{2}$的解,代表 particle 1 只有受到右邊的影響,左邊沒有(因為一起動)。
$\psi_-$
對於$\psi_-$來說,因為symmetry
\[\delta R_{-1} = - \delta R_{1}\]所以 EOM
\[\begin{cases} m\frac{d^2 \delta R_1}{dt^2} = -C(\delta R_1 - \delta R_2)-C(2\delta R_1)=-3C\delta R_1+C\delta R_2\\ m\frac{d^2 \delta R_2}{dt^2} = -C(\delta R_2 - \delta R_1) \end{cases}\]用 matrix 來解
\[\begin{pmatrix} m\omega^2 - C & C \\ C & m\omega^2 - 3C \end{pmatrix} \begin{pmatrix} \delta R_2 \\ \delta R_1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}\] \[\Rightarrow \omega^4-4\frac{C}{m}\omega^2+3\frac{C^2}{m^2}-\frac{C^2}{m^2}=0\\ \Rightarrow \omega^4-4\frac{C}{m}\omega^2+2\frac{C^2}{m^2}=0\]得到兩個解答
\[\omega^2=\frac{4\frac{C}{m}\pm\sqrt{16\frac{C^2}{m^2}-8\frac{C^2}{m^2}}}{2}\]如果看 particle 1,可以看到會受到兩邊的力。(這裡就不繼續展開了)
重新檢視 Operator
我們前面定義的 reflection operator 是
\[\hat{P}\begin{pmatrix} \delta R_{2}\\\delta R_{1}\\\delta R_{-1}\\\delta R_{-2} \end{pmatrix}\equiv \begin{pmatrix} \delta R_{-2}\\\delta R_{-1}\\\delta R_{1}\\\delta R_{2} \end{pmatrix}\]但其實更準確一點的表示應該是
\[\hat{Q}\begin{pmatrix} \delta R_{2}\\\delta R_{1}\\\delta R_{-1}\\\delta R_{-2} \end{pmatrix}\equiv \begin{pmatrix} -\delta R_{-2}\\-\delta R_{-1}\\-\delta R_{1}\\-\delta R_{2} \end{pmatrix}\]$\hat{Q}$表示的比較直覺,因為我們對於 reflection 就是鏡像對應差個負號,跟$\hat{P}$的差別是
\[\hat{P} = -\hat{Q}\]不過取平方之後都一樣,所以最後的答案不會變。
但是!!
畢竟看起來是不同的數學表示,那我們做的$\hat{P}$到底是什麼呢?
我們做的$\hat{P}$其實並不是空間上displacement做反轉,而是在做relabeling particle!
所以$\hat{P}$和$\hat{Q}$是在做一樣的事情,就是 relabel 之後,axis再轉一遍而已。
