(17) 變分 Hamiltonian Variational Principle
我們知道變分是更基本的原則,那就一起來看一下Hamiltonian的變分形式吧!
推導
設真實的軌跡為$q^* , p^* $
\[H^*\equiv H(q^*,p^*,t)\\ \diff{q^*}{t}=\pdv{H^*}{p^*}, \quad dq^*=\pdv{H^*}{p^*}dt\\ \diff{p^*}{t}=-\pdv{H^*}{q^*}, \quad dp^*=-\pdv{H^*}{q^*}dt\]現在要做的是H的變分,所以讓$(\delta{q},\delta{p})$是任意的微小變量函數(function of t)
\[\begin{align*} \delta{H}&\equiv{H}(q^*+\delta{q},p^*+\delta{p},t)-H(q^*,p^*,t)\\ &=\delta{q}\pdv{H^*}{q^*}+\delta{p}\pdv{H^*}{p^*} \end{align*}\]再考慮
\[\begin{align*} \delta{p}dq^*-\delta{q}dp^* &=\delta{p}\pdv{H^*}{p^*}dt-\delta{q}\left(-\pdv{H^*}{q^*}\right)dt\\ &=\left(\delta{p}\pdv{H^*}{p^*}+\delta{q}\pdv{H^*}{q^*}\right)dt\\ &=\delta{H}dt \end{align*}\]結合以上可以知道,若我們真的對真實軌跡做變分,則
\[\delta{p}dq^*-\delta{q}dp^*-\delta{H}dt=0\]為了希望能得到標準的$\delta\left(\int_{0}^{T}\cdots\right)=0$的形式,從上式出發推導
\[\begin{align*} &\int_{0}^{T}\left(\delta{p}dq^*-\delta{q}dp^*-\delta{H}dt\right)=0\\ &=\int_{0}^{T}\delta(pdq)-p^*\delta(dq)-\delta{qdp^*}-\delta{H}dt\quad(\because \delta(pdq)=\delta{pdq^*}+p^*\delta(dq))\\ &=\int_{0}^{T}\delta(pdq)-p^*d(\delta{q})-\delta{qdp^*}-\delta{H}dt\\ &=\int_{0}^{T}\delta(pdq-Hdt)-\int_{0}^{T}(p^*d(\delta{q})+\delta{q}dp^*)\\ &=\int_{0}^{T}\delta(pdq-Hdt)-\int_{0}^{T}d(p^*\delta{q})\\ &=\left(\delta\int_{0}^{T}(pdq-Hdt)\right)-p^*\delta{q}\bigg|_{t=0}^{t=T}\\ &=\delta\int_{0}^{T}(pdq-Hdt) = 0\\ \end{align*}\]最後一行因為變量在終端點為零 $$ \delta{q}(t=0)=0\\ \delta{q}(t=T)=0 $$ 但是注意這裡只有對$q$的邊界條件有限制。 如果邊界條件是$p$的話,那就會另外求出$\int qdp$的公式。
另外還有一點提醒,$d$什麼的時候都是沿著該路徑變化,$\delta$什麼的時候才是人為的移開原本路徑。
小結
整理對所有任意且微小變化量
\[\delta{q}\\ \delta{p}\]且邊界條件
\[\delta{q}(0)=\delta{q}(T) = 0\]則
\[\delta\int_{0}^{T}(pdq-Hdt)=0\]畫圖囉!(注意圖中只有對$q$的邊界條件有限制)
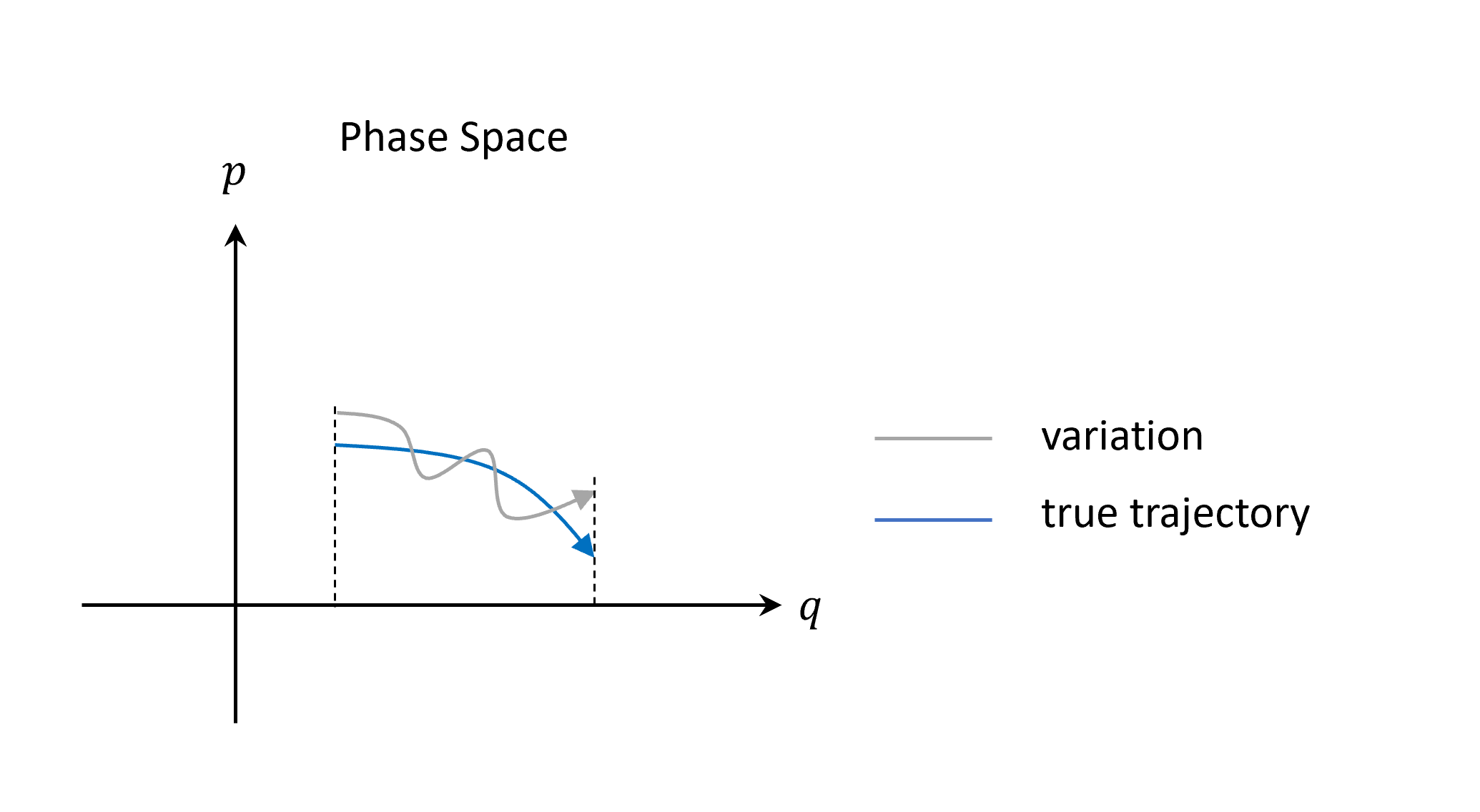
所有變分形式
1. $\delta\int_{0}^{T}(pdq-Hdt)=0$
前面推導的就是一般我們在 Phase Space$(q,p)$的平面,真實軌跡會滿足
\[\delta\int_{}^{}pdq-Hdt=0\]邊界條件為
\[\left\{ \begin{array}{ll} \delta q(t=0) = 0\\ \delta q(t=T) = 0 \end{array} \right.\]注意這裡的$q$其實可以有很多個成分$q_1, q_2, …, q_N$,所以更廣義的寫法是換成向量式的。不過即使是向量的寫法,也不需要有同樣的因次(e.g., 球座標,有$r$有$\theta$,有距離有角度):
\[\delta\int\vec{p}\cdot d\vec{q}-Hdt = 0\]2. $\delta\int_{0}^{T}(-qdp-Hdt)=0$
如果問題比較關注在$p$,或是邊界條件是鎖定$p$,可以改寫成這樣
\[\delta\int -qdp-Hdt=0\]邊界條件為
\[\left\{ \begin{array}{ll} \delta p(t=0) = 0\\ \delta p(t=T) = 0 \end{array} \right.\]驗證一下
\[\begin{align*} \delta\int -qdp-Hdt = &0\\ =& \int-\delta{q}dp^*-q^*d\delta{p}-\delta{H}dt\\ =&\int -\delta{q}dp^*-\left(d(q^*\delta{p})-\delta{p}dq^*\right)-\left(\pdv{H}{q^*}\delta{q}+\pdv{H}{p^*}\delta{p}\right)dt\\ =&\int -\delta{q}dp^*-q^*\delta{p}\bigg|_0^T+\delta{p}dq^*-\left(\pdv{H}{q^*}\delta{q}+\pdv{H}{p^*}\delta{p}\right)dt\\ \quad&(\because \delta p(T)=\delta p(0)=0)\\ =&\int -\delta{q}dp^*+\delta{p}dq^*-\left(\pdv{H}{q^*}\delta{q}+\pdv{H}{p^*}\delta{p}\right)dt)\\ =&\int \delta{q}\left(-dp^*-\pdv{H}{q^*}dt\right)+\delta{p}\left(dq^*-\pdv{H}{p^*}dt\right)\\ \end{align*}\]$\because \delta{q}, \delta{p}$為任意的微小變化量,得證原本的Hamiltonion’s equation of motion(EOM)
\[\left\{ \begin{array}{ll} dp^* = -\pdv{H}{q^*}dt\\ dq^* = \pdv{H}{p^*}dt \end{array} \right.\]3. $\delta\int_{0}^{T}(pdq-Hdt)=0$
上述兩個是在phase space$(q,p)$,現在推廣到 extended phase space$(q,p,t)$,就像第十三節一樣,用更廣的角度去看,把t軸拉出來,可以看到更清楚的軌跡。
所以這個看似和第1點一樣的公式,但可以進一步看得更多。
所以我們重新定一個方便且可描述軌跡的參數$s\in[0,1]$,使成$q=q(s), p=p(s), t=t(s)$,把t當作independent variable,所以改寫成:
\[\delta\int pdq-Hdt=0\]邊界條件為
\[\left\{ \begin{array}{ll} \delta q(s=0) = \delta q(s=1) = 0\\ \delta t(s=0) = \delta t(s=1) = 0 \end{array} \right.\]驗證一下
\[\begin{align*} \delta\int pdq-Hdt = &0\\ =&\int \delta{p}dq^*+{p^*d\delta{q}}-\left(\pdv{H}{q^*}\delta{q}+\pdv{H}{p^*}\delta{p}+\pdv{H}{t^*}\delta{t}\right)dt^*-{H^*d\delta{t}}\\ =&\int\delta{p}dq^*+{\left(d(p^*\delta{q})-\delta{q}dp^*\right)}-\pdv{H}{q^*}\delta{q}dt^*-\pdv{H}{p^*}\delta{p}dt^*-\pdv{H}{t^*}\delta{t}dt^*-{(d(H^*\delta{t})-\delta{t}dH^*)}\\ =&\int\delta{p}dq^*+{\left(p^*\delta{q}\bigg|_0^1-\delta{q}dp^*\right)}-\pdv{H}{q^*}\delta{q}dt^*-\pdv{H}{p^*}\delta{p}dt^*-\pdv{H}{t^*}\delta{t}dt^*-{\left(H^*\delta{t}\bigg|_0^1-\delta{t}dH^*\right)}\\ =&\int\delta{p}\left(dq^*-\pdv{H}{p^*}dt^*\right)+\delta{q}\left(-dp^*-\pdv{H}{q^*}dt^*\right)+\delta{t}\left(-\pdv{H}{t^*}+dH^*\right)\\ \end{align*}\]$\because \delta{q}, \delta{p},\delta{t}$ 為任意的微小變化量,得證相似的Hamiltonion’s equation of motion(EOM)
\[\left\{ \begin{array}{ll} dp^* = -\pdv{H}{q^*}dt^*\\ dq^* = \pdv{H}{p^*}dt^*\\ dH^* = \pdv{H}{t^*}dt^* \end{array} \right.\]最後一項其實就是守恆量第十八節的,但現在用更廣的去看,也是natural consistence。
意義
把t引進來之後,variation的自由度更大,可以想像成原本在0.5秒走到A點,但現在可以變動成為0.51秒走到,或是0.48秒就走到,在空間位置不變的情況下,到達時間不同,這是自由度大的其中一點。
另外一個自由度大的點,是在傳統的軌跡裡面,你是可以在第10秒的時候到,然後去第11秒玩一玩,再回10秒的位置(見下面的比較圖),自由度變得超大。等於是在整條軌跡裡面,只要保持邊界條件的限制,你都可以到未來或過去玩一玩再回來!
4. $\delta\int_{0}^{T}(pdq+tdH)=0$
從上面可以再改寫成:
\[\delta\int pdq+tdH=0\]邊界條件為
\[\left\{ \begin{array}{ll} \delta q(s=0) = \delta q(s=1) = 0\\ \delta H(s=0) = \delta H(s=1) = 0 \end{array} \right.\]驗證就留給大家自行驗證。
意義
現在H也可以改變,意義在於只要滿足H的邊界條件,現在起始點和終點的t都已經沒有限制在0和T(假設10秒),你可以是-0.03秒開始,可以是10.003秒結束,自由度也變得非常大!
圖像比較
我們可以簡單畫一個圖把上面的四個例子再整理一下
(藍色為true trajectory,灰色為variation)
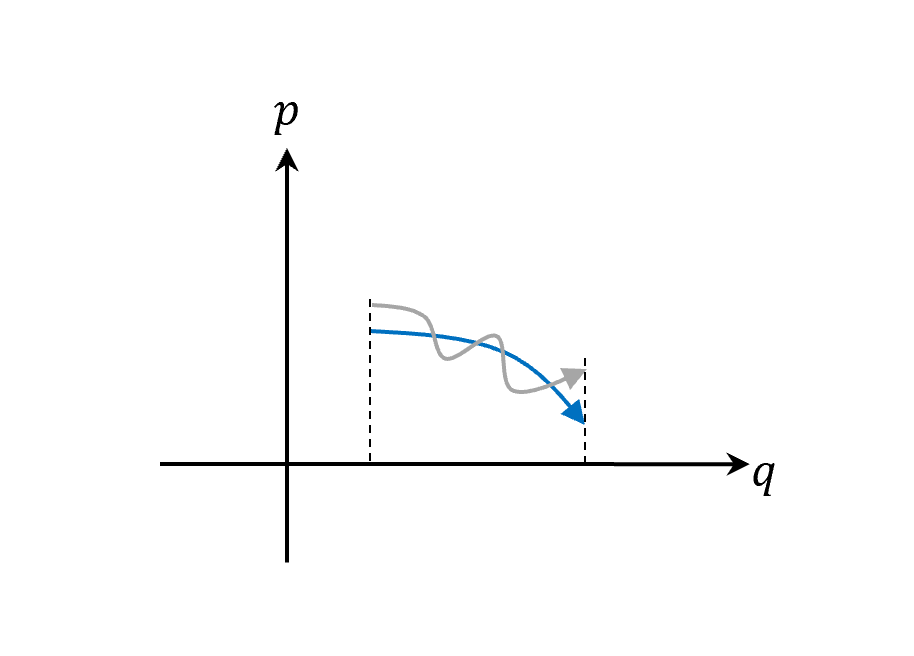 |
$\delta\int_{}^{}pdq-Hdt$ $\delta q(t=0) = \delta q(t=T) = 0$ |
 |
$\delta\int -qdp-Hdt$ $\delta p(t=0) = \delta p(t=T) = 0$ |
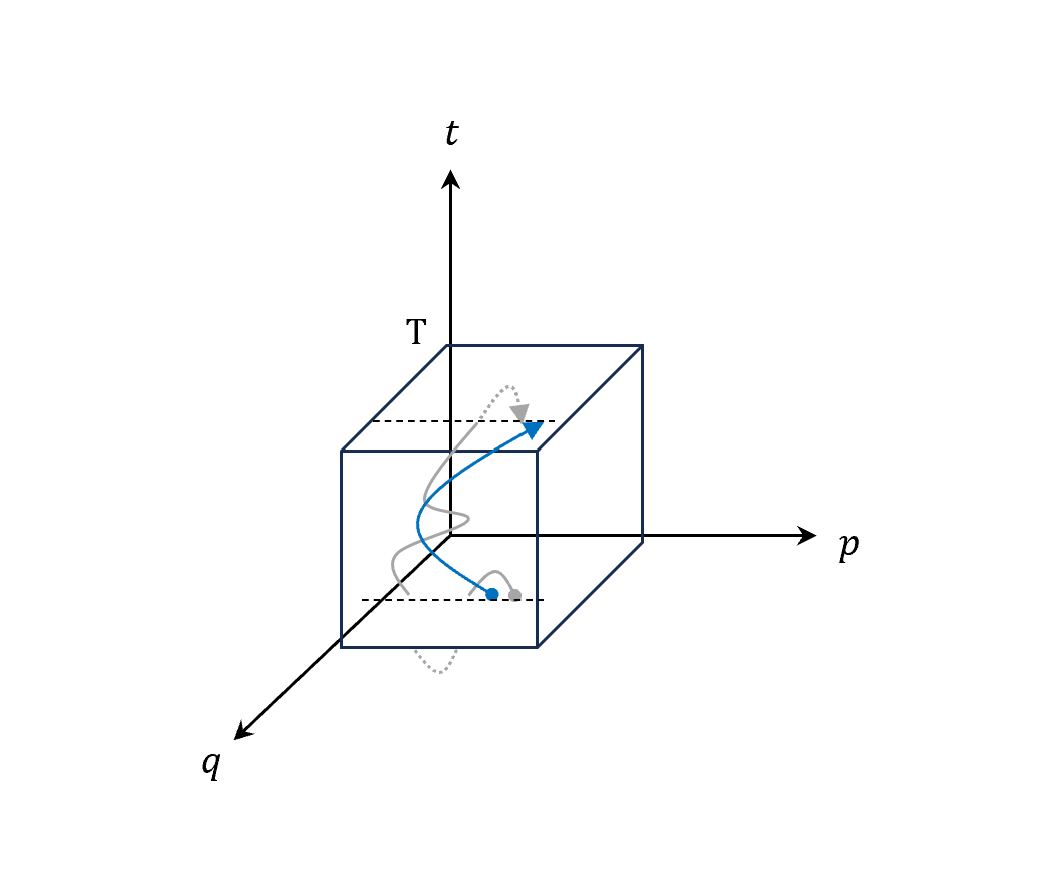 |
$\delta\int pdq-Hdt$ $\delta q(s=0) = \delta q(s=1) = 0$ $\delta t(s=0) = \delta t(s=1) = 0$ |
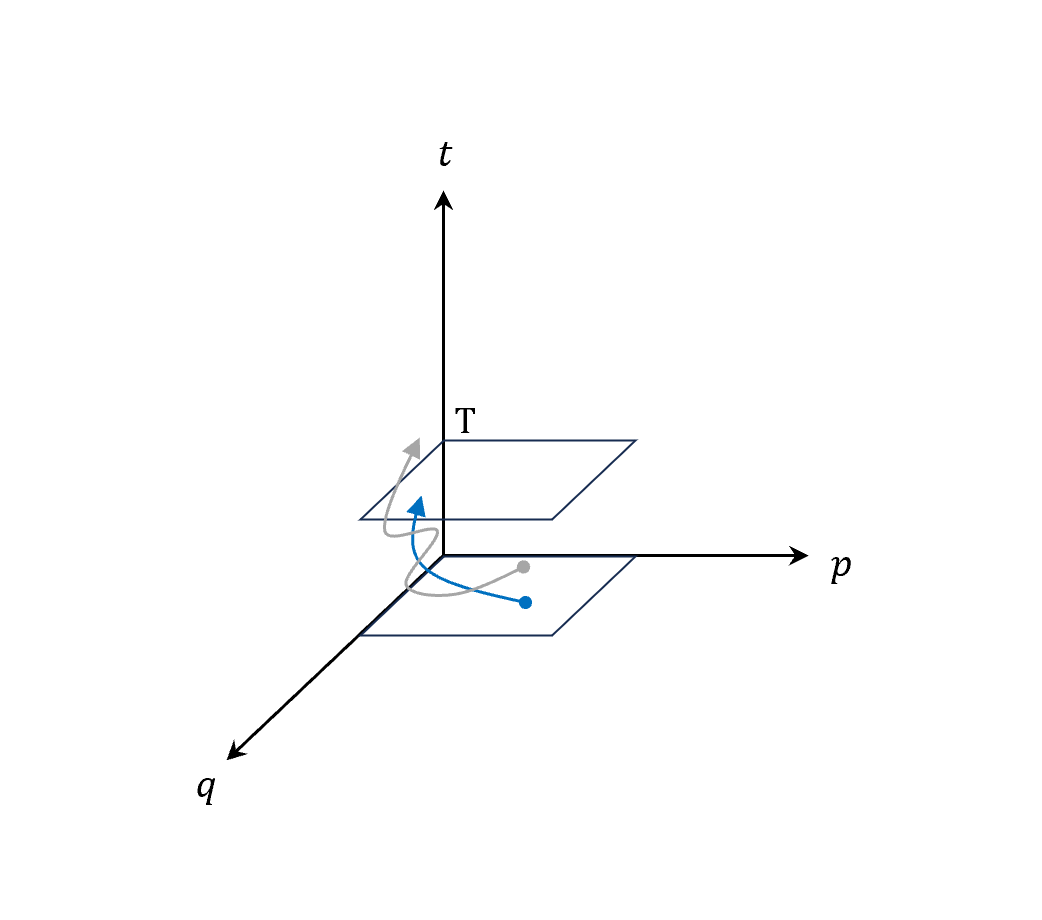 |
$\delta\int pdq+tdH$ $\delta q(s=0) = \delta q(s=1) = 0$ $\delta H(s=0) = \delta H(s=1) = 0$ |
