(21) 變分 Adiabatic Invariant

前言

現在想像一下有一個單擺在做SHO，我們慢慢將繩子拉起來使得單擺長度變短，頻率會變，能量也會變，這時對應的Hamiltonian就會隨著時間有緩慢的變化，因此我們先假設將$H$的形式定為

\[H(q,p,\tau), \quad \tau=\epsilon{t}\]

其中$\tau$是第三個參數，$\epsilon$是定值，所以隨時間變動$\tau$會跟著改變。

舉例

\[H=\frac{p^2}{2m}+\frac{m\omega^2}{2}q^2(1-\tau)+\tau{A}q^4\]

• 第二項：代表隨著時間增加，會緩慢地影響整個系統的自然頻率(natural frequency)。
• 第三項：假設A是大於0的常數，因此隨著時間增加，會有一個非線性的變化(但最後還是能拉回來)。

因此隨著時間變化，我們可以看到幾件事情：

1. 隨著時間增加，$H$每次都會改變$\mathcal{O}(\epsilon)$，當時間變化量是$\mathcal{O}(\frac{1}{\epsilon})$的時候，$H$的改變量就會是$\mathcal{O}(1)$($\because\tau=\epsilon{t}\rightarrow\epsilon\times\frac{1}{\epsilon}$)。

2. 當$\tau$在特定時間點是固定值的時候，$H$也是固定守恆量。對應本例SHO，就是一個特定的能量，所以在這個時間點有自己一整套週期性的解答。

3. SHO不同能量有不同的解答，所以整個系統在每個特定時間點的$\tau$，會有自己對應一整套的週期性解答(a family of periodic solutions)。

小結就是這個系統隨著時間一直在變化，$H$和$\tau$也在變化。

而我們接下來要做的事情就是

• t=0的時候，記下$p,q,\tau$數值，做為參考系統一，積一圈$\oint{pdq}$得到第一個數值。
• t=1的時候，記下$p,q,\tau$數值，做為參考系統二，積一圈$\oint{pdq}$得到第二個數值。

繼續紀錄下去，預期在經過$\mathcal{O}(\frac{1}{\epsilon})$時間後，這個積一圈的$\oint{pdq}$的物理量和最一開始要相差$\mathcal{O}(1)$。

但是！

我們會發現積一圈$\oint{pdq}$的物理量，可以只差到$\mathcal{O}({\epsilon})$！

這個，我們就稱為Adiabatic Invariant。

(當然現在這樣想會有點奇怪，因為這個每個紀錄的參考系統根本就不存在，真正實際的系統一定是一直在隨著時間變化的。)

If we allow the system to evolve for a very long time, i.e., of order $\mathcal{O}(\frac{1}{\epsilon})$ then quite generally we would expect a physical quantity of the system to have changed by order of $\mathcal{O}(1)$.

But the adiabatic invariant we will introduce next actually only changes by the amount of $\mathcal{O}(\epsilon)$.

That physical quantity is $\oint{pdq}$ complete circuit for a fixed $\tau$.

猜想

接下來我們猜想兩點，預期的$\mathcal{O}(1)$，和實際的$\mathcal{O}(\epsilon)$，會有什麼邏輯在裡頭。

預期的 $\mathcal{O}(1)$

按照前言例子和紀錄方式，我們紀錄的點是SHO回到原點的數值，所以

• $q^*(t)$ 會在時間$t_0, t_1,…,t_n$回到起始值(還是盪回來)。
• $p^*(t)$ 會在時間$t_0, t_1,…,t_n$，非常接近上一個數值(繩子變了速度有點變了)。
• 因為實際的演化$H$一直在變動，所以並非一定時間等間隔($t_1-t_0\neq t_2-t_1$)，代表每次回來的時間(盪一次)不會完全一樣，但預期還是要很接近$\tau$對應的週期，所以$t_j-t_{j-1}=\mathcal{O}(1)$。

因此預期假設一個物理量$f_t$隨著時間演化會是

\[\left\{ \begin{array}{ll} f_{t_{1}}-f_{t_{0}}=\mathcal{O}(\epsilon)\\ f_{t_{2}}-f_{t_{1}}=\mathcal{O}(\epsilon)\\ \vdots\\ f_{t_{n}}-f_{t_{n-1}}=\mathcal{O}(\epsilon) \end{array} \right.\]

總結一段時間內所有的改變量(# of terms = $\mathcal{O}(\frac{1}{\epsilon})$)

\[\Rightarrow f_{t_{n}}-f_{t_{0}}=\mathcal{O}(\epsilon)+\mathcal{O}(\epsilon)+\cdots+\mathcal{O}(\epsilon)=\mathcal{O}(1)\]

實際的 $\mathcal{O}(\epsilon)$

但或許實際上物理量$f_t$隨著時間變化應該要變成 $f_{t_{j}}-f_{t_{j-1}}=\mathcal{O}(\epsilon^2)$。

所以一段時間內所有的改變量(# of terms = $\mathcal{O}(\frac{1}{\epsilon})$)

\[f_{t_{n}}-f_{t_{0}}=\mathcal{O}(\epsilon^2)+\mathcal{O}(\epsilon^2)+\cdots+\mathcal{O}(\epsilon^2)=\mathcal{O}(\epsilon)\]

不過有個很重要的釐清點！

這裡算$f_{t_{j}}-f_{t_{j-1}}$是$q$回到原點的時間，若挑的時間點剛好是$t_j\ge{t}\ge{t_{j-1}}$，依然$f_{t}-f_{t_{j-1}}=\mathcal{O}(\epsilon)$。

只有$t=t_j$，$q$回到一樣的位置，$q_t = q_{t_j}=q_{t_{j-1}} $的時候，才是$f_{t_{j}}-f_{t_{j-1}}=\mathcal{O}(\epsilon^2)$。

證明

那我們就來實際推導證明吧！看到底為啥可以有猜想二的結果。

假設固定$\tau(\tau=\epsilon t)$和給定能量$E(=H(q,p,\tau))$，定

\[J\equiv\oint{pdq}\]

在phase space會是等能量曲線。

現在要來做變分，所以拓展到extended phase space，$q,p,t$都可以變化，只是這裡一樣限制自由度，做partial的變化。

不多說，先上圖。

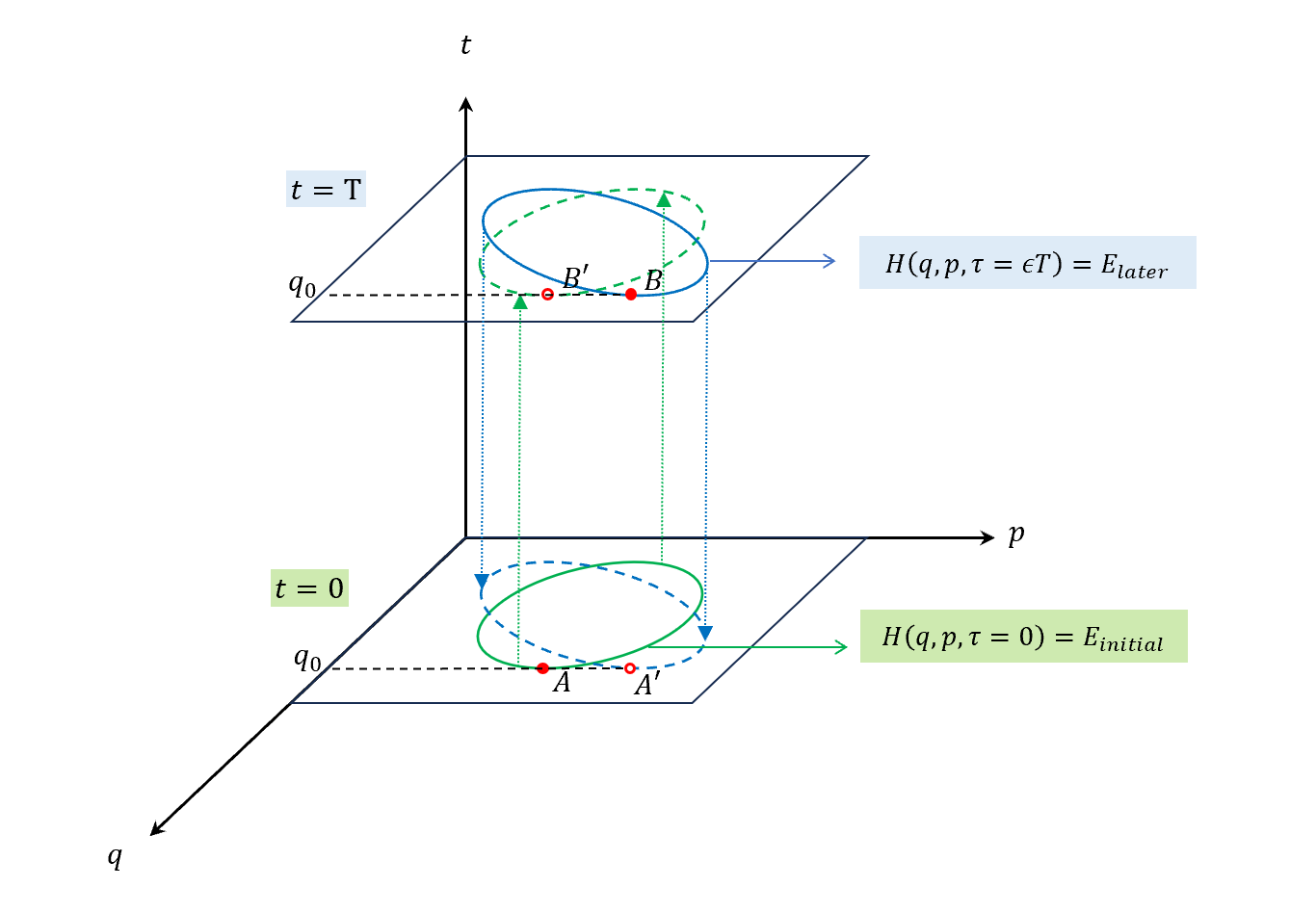
現在整個系統的時間是一直在走的，$H$一直在變，所以是從$t=0$走到$t=T$，從$A$點螺旋上去走到$B$點，

而我們現在畫圖就類似截圖的概念，在$t=0$和$t=T$各截一張，並畫出各自的$\oint{pdq}$。

• $t=0$的時候，畫綠線，往上投影到$t=T$的綠色虛線。
• $t=T$的時候，畫藍線，往下投影到$t=0$的藍色虛線。

注意，我們有強調一次週期要算的是回到起始位置(盪一次回來)，所以可以看到經過時間$T$之後對應的$q$軸會是一樣的，但$p$就不需要了，只是預期

\[p(t=T)-p(t=0)=\mathcal{O}(\epsilon)\]

(可以想像，把前言的$H$公式做$\diff{p}{t}=-\pdv{H}{q}$計算，則$p$的變化量也是$\mathcal{O}(\epsilon)$。)

做變分

因為真實軌跡可以想像就是從綠色變成藍色，所以我們可以有兩種變法

• 都維持在綠色(起始)的柱狀，會從$A$繞到$B’$，定為$\gamma{1}$
• 都維持在藍色(最後)的柱狀，回推$B$繞到$A’$，定為$\gamma{2}$

確認邊界條件$q$都沒有變就可以了。

接著真實軌跡和變分的軌跡關係式(記得最早說過的變分取極值的概念，$\delta$() = 0)

\[\int_{\text{true}}^{}pdq-Hdt\\ =\int_{\gamma{1}}pdq-Hdt+\mathcal{O}(\epsilon^2)\\ =\int_{\gamma{2}}pdq-Hdt+\mathcal{O}(\epsilon^2)\]

因為end point condition是$\mathcal{O}(\epsilon)$，integral後就是$\mathcal{O}(\epsilon^2)$。

(這裡還有點疑惑，但因為真實軌跡積起來的動量前面說到是差$\mathcal{O}(\epsilon)$，而變分這裡因為是圓柱狀直接對應，$p$沒差，所以的確相較於真實軌跡會差$\mathcal{O}(\epsilon)$，所以積分完就是二次。)

移項

\[\int_{\gamma{2}}pdq-\int_{\gamma{1}}pdq=\int_{\gamma{2}}Hdt-\int_{\gamma{1}}Hdt+\mathcal{O}(\epsilon^2)\]

注意這裡的積分是繞著柱狀螺旋上去的軌跡，但我們從最上面俯視看的話，可以看到就是一個平面的二維曲線，所以改寫成circular integral

\[\oint_{\text{at } t=T}pdq-\oint_{\text{at }t=0}pdq=\int_{\gamma{2}}Hdt-\int_{\gamma{1}}Hdt+\mathcal{O}(\epsilon^2)\]

Note:
複習一下泰勒展開 $$ f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x - a)^n $$

綠色$\gamma{1}$

在$t=0$做泰勒展開

\[\int_{\gamma{1}}H(q,p,\tau=\epsilon{t})dt\\ =\int \left(H(q,p,0)+\pdv{H(q,p,\tau)}{\tau}\epsilon{t}\right)dt+\mathcal{O}(\epsilon^2)\\ =E_{\text{initial}}\cdot{T}+\epsilon\int\pdv{H(q,p,\tau)}{\tau}\bigg|_{\tau=0}^{}tdt+\mathcal{O}(\epsilon^2)\]

藍色$\gamma{2}$

在$t=T$做泰勒展開

\[\int_{\gamma{2}}H(q,p,\tau=\epsilon{t})dt\\ =\int_{\gamma{2}}H(q,p,\tau=\epsilon(T+t-T))dt\\ =\int \left(H(q,p,\epsilon{T})+\pdv{H}{\tau}\epsilon{(t-T)}\right)dt+\mathcal{O}(\epsilon^2)\\ =E_{\text{final}}\cdot{T}+\epsilon\int\pdv{H(q,p,\tau)}{\tau}\bigg|_{\tau=\epsilon{T}}^{}(t-T)dt+\mathcal{O}(\epsilon^2)\\ =E_{\text{final}}\cdot{T}+\epsilon\int\pdv{H(q,p,\tau)}{\tau}\bigg|_{\color{red}{\tau=0}}^{}(t-T)dt+\mathcal{O}(\epsilon^2)\]

這裡微分的at數值變了，是因為本來$\tau=\epsilon{T}$和$\tau=0$的時候，就會差$\epsilon$，所以有二次項的地方都收集到最後面的$\mathcal{O}(\epsilon^2)$。

結合

\[\begin{align} \int_{\gamma{2}}Hdt-\int_{\gamma{1}}Hdt=& (E_\text{final}-E_\text{initial})T\\ &+\epsilon\int_{\gamma{2}}\pdv{H(q,p,\tau)}{\tau}\bigg|_{\tau=0}^{}(t-T)dt\\ &-\epsilon\int_{\gamma{1}}\pdv{H(q,p,\tau)}{\tau}\bigg|_{\tau=0}^{}tdt\\ &+\mathcal{O}(\epsilon^2)\\ =& (E_\text{final}-E_\text{initial})T\\ &+\epsilon\int_{\color{red}{\gamma{1}}}\pdv{H(q,p,\tau)}{\tau}\bigg|_{\tau=0}^{}(t-T)dt\\ &-\epsilon\int_{\gamma{1}}\pdv{H(q,p,\tau)}{\tau}\bigg|_{\tau=0}^{}tdt\\ &+\mathcal{O}(\epsilon^2)\\ =& (E_\text{final}-E_\text{initial})T+\epsilon\int_{\gamma{1}}\pdv{H(q,p,\tau)}{\tau}\bigg|_{\tau=0}^{}(-T)dt+\mathcal{O}(\epsilon^2)\\ =&(E_\text{final}-E_\text{initial})T-T\int_{\gamma{1}}\epsilon\pdv{H}{\tau}dt+\mathcal{O}(\epsilon^2)\\ =&(E_\text{final}-E_\text{initial})T-T\int_{\gamma{1}}\pdv{H}{t}dt+\mathcal{O}(\epsilon^2)\\ =&T\left[(E_\text{final}-E_\text{initial})-\int_{\gamma{1}}\pdv{H}{t}dt\right]+\mathcal{O}(\epsilon^2)\\ =&T\cdot{0}+\mathcal{O}(\epsilon^2)\\ =&\mathcal{O}(\epsilon^2) \end{align}\]

推導過程解釋幾個

• 第二個等號：因為$\gamma{2}$改$\gamma{1}$差別是$\mathcal{O}(\epsilon)$，搭配前面的係數$\epsilon$，收集起來的二次項一樣可以放到後面$\mathcal{O}(\epsilon^2)$。
• 第五個等號：$\tau=\epsilon{t}$
• 最後一個等號：$\diff{H}{t}=\pdv{H}{t}\Rightarrow\Delta{H}=\int_{0}^{T}\pdv{H}{t}dt$

得證

很棒！那整理一下就是

\[\oint_{\text{at } t=T}pdq-\oint_{\text{at }t=0}pdq=\int_{\gamma{2}}Hdt-\int_{\gamma{1}}Hdt+\mathcal{O}(\epsilon^2)=\mathcal{O}(\epsilon^2)\]

用我們定義的$J$就是

\[J\bigg|_{\text{when q has come back}}^{}=J\bigg|_{\text{q=initial}}^{}+\mathcal{O}(\epsilon^2)\]

(附註一下，這全部的推導過程中，我都把二階項留了下來，但原始筆記有些有漏掉，但覺得應該這樣比較合理。)

證實之前的猜想二，每一次週期回來原本的位置，都會差二次數量級，而累積長時間之後(up to $\mathcal{O}(\frac{1}{\epsilon})$)，就會差$\mathcal{O}(\epsilon)$而不是$\mathcal{O}(1)$

\[J(t=\mathcal{O}(\frac{1}{\epsilon}))-J(t=0)=\mathcal{O}(\epsilon)\text{ only!!}\]

小結

再順一下思路，我們原本預設的$H$每次都要差$\mathcal{O}(\epsilon)$，所以$\mathcal{O}(\frac{1}{\epsilon})$會差$\mathcal{O}(1)$，認為在這個系統中，應該也都遵循著這個形式，物理量都差$\mathcal{O}(1)$。

但是發現有一個adiabatic invartiant的物理量$\oint pdq$，每次只差$\mathcal{O}(\epsilon^2)$，所以$\mathcal{O}(\frac{1}{\epsilon})$之後只差$\mathcal{O}(\epsilon)$。

舉例

我們舉最常見的單擺SHO，假設現在我們偷偷慢慢拉繩子，所以公式類似這樣

\[\frac{d^2\theta}{dt^2}+\frac{g}{l(t)}\theta=0\\ (\text{$l$ varied by t})\]

那$H$公式

\[H=\frac{p^2}{2m}+\frac{m\omega^2}{2}q^2=E\\ (\omega=\omega(\tau)\text{ depends on the time t})\]

代入Adiabatic Invariant

\[\begin{align} J=\oint{pdq}&=2\int_{qmin}^{qmax}\sqrt{2m\left(E-\frac{m\omega^2}{2}q^2\right)}dq\\ &=4\int_{0}^{qmax}\sqrt{2m\left(E-\frac{m\omega^2}{2}q^2\right)}dq \end{align}\]

變數變換

\[q\equiv\sqrt{\frac{2E}{m\omega^2}}\xi\\ \xi\equiv\sin\theta\]

代回去

\[\begin{align} J&=4\int_{0}^{1}\sqrt{2mE}\sqrt{\frac{2E}{m\omega^2}}\sqrt{1-\xi^2}d\xi\\ &=\frac{8}{\omega}E\int_{0}^{1}\sqrt{1-\xi^2}d\xi\\ &=\frac{8E}{\omega}\frac{1}{2}\cdot\frac{\pi}{2}\\ &=E\cdot\frac{2\pi}{\omega}\\ &=\frac{E}{\nu}\quad(\nu\text{: wanted frequency}) \end{align}\]

前面證明過，經過很長時間累積，最後和最初相差只有$\mathcal{O}(\epsilon)$，也就是

\[\oint_{\text{after a long time}}{pdq}=\frac{E_{\text{final}}}{\nu_{\text{final}}}\approx\oint_{\text{initial}}{pdq}=\frac{E_{\text{initial}}}{\nu_{\text{initial}}}\]

因為$\omega(t)$可以根據給予的情況而變，所以其實$\nu_{\text{initial}}$和$\nu_{\text{final}}$可以差別很大，$E_{\text{initial}}$和$E_{\text{final}}$也可以差別很大，但是重點在於兩者最後比比值相近

\[\frac{E_{\text{final}}}{\nu_{\text{final}}}\approx\frac{E_{\text{initial}}}{\nu_{\text{initial}}}\]

這個就有趣了！我們留到下章節在講！