(20) 變分 Hamiltonian Maupertuis’ Principle with Kepler orbit examples
前言
我們之前的筆記中,都是在講如何知道有時間演化的系統動態(dynamic of the system),但這節我們不關心這個,不關心某個時間點在哪個位置,只關心整個軌跡形狀(shape in the configuration space $\vec{q}$)。
更簡單地說,就是在與時間無關的情況下,用變分的方法來決定在configuration space下的軌跡形狀。
因此現在對Hamiltonian有三大假設
假設一:$H$與時間無關
\[H\equiv a \text{ (constant)}\]The Hamiltonian H has no explicit time dependence, so that $H\equiv a$ constant on the true trajectory.
假設二:變化量的限制
因為$H$不變,如同能量不變,整個變分軌跡上的$H$都要一樣,因此做變分時,若$q$改變,$p$和$t$能變的就有限,自由度下降。
In view of 1, we thus restrict ourselves to variations $(q,p,t)$ in the extended phase space which keep H = const.
假設三:需保持的$p-q$關係式
對真實軌跡來說,我們知道
\[\diff{q^*}{t}=\pdv{H}{p^*}\]對特定Hamiltonian形式
\[H=\frac{1}{2}\vec{p}^t\cdot\frac{1}{\hat{M_1}}\cdot\vv{p}+V\qquad{\hat{M_1}\text{: contain $\vv{q}$-dependence}}\\ \pdv{H}{p^*}=\frac{1}{\hat{M_1}}\vv{p}\\ \Rightarrow d\vv{q}^*\propto\frac{1}{\hat{M_1}}\vv{p^*}\]因此多加的限制是,即便$q$和$p$做微小的任意變動,也不能胡作非為,必須保持
\[d\vec{q}\propto\frac{1}{\hat{M_1}}\vv{p}\]的關係式。
Symbol: $$ \hat{M}=\hat{M}(\vv{q})\\ \vv{q}\rightarrow{q}^j\quad j=1,2,...,N\text{ component of }\vv{q}\\ \vv{p}\rightarrow{p}_j\\ $$ Einstein's summmation: $$ \int p_j dq^j - Hdt\\ p_j dq^j\Leftrightarrow \sum_{j=1}^{N}p_j dq^{j} $$ Hamiltonian of form: $$ H=\frac{1}{2}\vv{p}^t\cdot\frac{1}{\hat{M}}\cdot\vec{p}+V(\vv{q})\\ =\sum_{jk}^{}\frac{1}{2}p_j\left(\frac{1}{\hat{M}}\right)^{jk}p_k+V\\ \Rightarrow\frac{1}{2}p_j\left(\frac{1}{\hat{M}}\right)^{jk}p_k+V $$ Others: $$ d:\text{ difference between points in one trajectory}\\ \delta:\text{ difference between varid trajectory and true trajectory} $$
Jacobi’s Form
我們直接來看,一般真實的軌跡
\[\diff{\vv{q}^*}{t}=\pdv{H}{\vv{p}^*}=\frac{1}{\hat{M}}\vv{p}^*\]而變分的軌跡,通常選定$q$之後,$t$可以是自由的,然後$p$就可以被決定下來。
但我們需要滿足前言說的,$H$維持定值
\[H(q,p)=H(q^*,p^*)\]以及維持$p-q$關係式
\[\diff{\vv{q}}{t}=\frac{1}{\hat{M}}\vv{p}\]結合一下
\[\begin{align*} H&=\frac{1}{2}\vv{p}^t\cdot\frac{1}{\hat{M}}\cdot\vec{p}+V(\vv{q})\\ &=\frac{1}{2}\left(\hat{M}\diff{\vv{q}}{t}\right)^t\cdot\frac{1}{\hat{M}}\cdot\left(\hat{M}\diff{\vv{q}}{t}\right)+V\\ &=\frac{1}{2}\diff{\vv{q}^t}{t}\hat{M}\diff{\vv{q}}{t}+V\\ &\equiv E = \text{constant} \end{align*}\]所以其實$q$選定之後,$t$和$p$一開始就是被限制住的。
\[\frac{1}{dt}=\sqrt{\frac{2E-V(\vv{q})}{d\vv{q}^t\cdot\hat{M}\cdot d\vv{q}}}\]現在加入變分,這裡採用在extended phase space的公式
\[\delta\int\vv{p}\cdot d\vv{q}+tdH=0\]因為$dH=0$,注意這裡的$d$是同軌跡不同點之間的變化,繼續推導
\[\begin{align*} \delta\int\vv{p}\cdot d\vv{q} &=0\\ &\equiv\delta\int\vv{p}^t\cdot d\vv{q}\\ &=\delta\int\left(\hat{M}\diff{\vv{q}}{t}\right)^t\cdot d\vv{q}\\ &=\delta\int\frac{d\vv{q}^t\cdot{\hat{M}}\cdot d\vec{q}}{dt}\\ &=\delta\int{d\vv{q}^t\cdot{\hat{M}}\cdot d\vec{q}}\cdot{\sqrt{\frac{2E-V(\vv{q})}{d\vv{q}^t\cdot\hat{M}\cdot d\vv{q}}}}\\ &=\delta\int\sqrt{(2E-V(\vv{q}))d\vv{q}^t\cdot\hat{M}\cdot d\vv{q}}\\ &=\delta\int\sqrt{d\vv{q}^t\cdot(2E-V(\vv{q})\hat{M})\cdot d\vv{q}}\\ &\equiv\delta\int\sqrt{\sum_{jk}^{}dq^j g_{jk} dq^k}\\ &=\delta\int\sqrt{dq^j g_{jk}(\vv{q}) dq^k} \end{align*}\]其中
\[\int\sqrt{dq^j g_{jk}(\vv{q}) dq^k}\]就是Jacobi’s form of Maupertuis principle。
意義 ─ 距離最小值
Jacobi’s Form的意義在於,我們可以把軌跡$\vv{q}$視作是在另一個curved空間(抽象空間)的測地線(geodesic),代表點與點之間的最短距離,因為
\[\int\sqrt{dq^j g_{jk} dq^k}\]即為表示在多維空間中,點與點之間的距離長度。
舉例來說,在3-D Eulidean space,我們熟知的形式
\[ds=\sqrt{(dx)^2+(dy)^2+(dz)^2}\\ \Rightarrow s=\int\sqrt{(dx)^2+(dy)^2+(dz)^2}\]在球座標中就是
\[ds=\sqrt{(dr)^2+r^2(d\theta)^2+r^2\sin^2\theta(d\phi)^2}\\ \Rightarrow s=\int\sqrt{(dr)^2+r^2(d\theta)^2+r^2\sin^2\theta(d\phi)^2}\]都可表示成
\[\int\sqrt{\sum_{jk}^{}dq^j g_{jk}(\vv{q}) dq^k}\]在球座標中,$g_{jk}$就是diagonal矩陣,且都是$\vv{q}$的函數(1,$r^2, r^2sin^2\theta$)。
因此若要找距離的最小值
這就等價於什麼呢?
回顧一下,我們從基本的變分公式出發
\[\delta\int\vv{p}\cdot d\vv{q}+tdH=0\]在加上條件,需要滿足$H$不變,以及$p-q$關係式的前提下,上式等價於在求
\[{\delta\int(\vv{p}\cdot d{\vv{q}})=\delta\int\sqrt{\sum_{jk}^{}dq^j g_{jk}(\vv{q}) dq^k}=0}\]而我們對這個公式的理解,就是要找距離的最小值!
變分的概念+找距離的最小值再次完美地套用在這裡,神奇吧!
而這個Jacobi’s Form又說明什麼呢?
說明一般來說我們隨著取得座標越複雜,空間越扭曲,$g$就會越加複雜,所以我們能直接求得最短路徑的方式就會很艱難,可是Jacobi簡化這個方式,告訴我們,你會覺得點跟點之間的最短距離看起來彎曲,那是因為在你現在定的xyz座標裡長這個樣子,如果是在另外一個抽象的座標系統,對那個空間來說,就是求一個最短的直線距離(回想第一節求最短路徑就是直線的例子)。
這個想法甚至超前愛因斯坦,我們說光線是彎曲的,那是因為我們定的座標畫出來是這樣,但是實際上在彎曲的世界裡,就是走直線段!
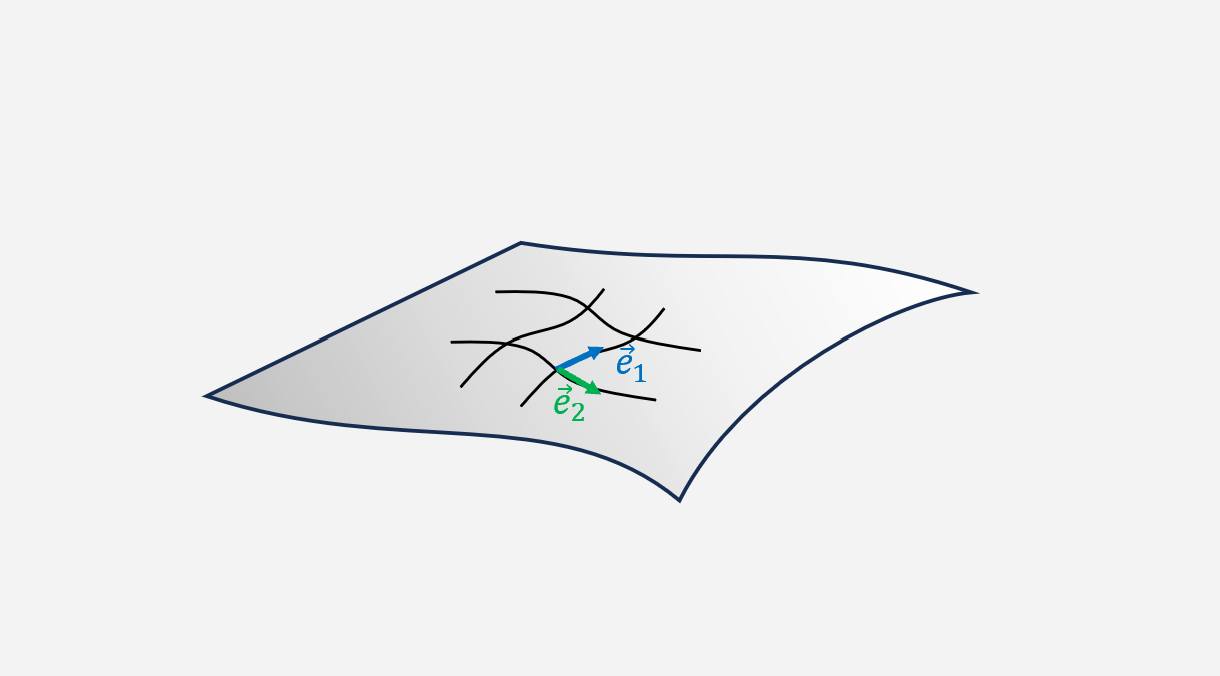
補充說明公式: 定local basis: $$ \vv{e_1}, \vv{e_2} $$ small displacement along the surface: $$ d\vv{q}\equiv dq^1\vv{e_1}+dq^2\vv{e_2} $$
變分證明克普勒的軌跡
接下來用兩個例子,證明克普勒的在configuration space是橢圓,在momentum space是正圓。
目的是要驗證前面說的,變分用部分的資訊得到軌跡形狀。
例子一:克普勒橢圓軌跡(configration space)
知2-D SHO:
\[H=\frac{m}{2}\left[\left(\diff{r}{t}\right)^2+\left(r\diff{\phi}{t}\right)^2\right]+\frac{m\omega^2}{2}r^2=E\]所以之前算過的
\[\int\sqrt{(2E-V(\vv{q}))d\vv{q}^t\cdot\hat{M}\cdot d\vv{q}}\\ =\int\sqrt{2\left(E-\frac{m\omega^2}{2}r^2\right)m\left((dr)^2+r^2(d\phi)^2\right)}\]我們把$r$ rescale 一下替換成$\zeta$,則上式就會正比於
\[\propto\int\sqrt{1-\zeta^2\left((d\zeta)^2+\zeta^2(d\phi)^2\right)}\\ =\int\sqrt{\left(\sqrt{1-\zeta^2}d\zeta\right)^2+\left(\sqrt{1-\zeta^2}\zeta d\phi\right)^2}\]同理2-D Keplerian:
\[V=-\frac{k}{r}\qquad E=\text{negative}\\ \int\sqrt{2\left(E-\left(-\frac{k}{r}\right)\right)m\left((dr)^2+(rd\phi')^2\right)}\\ \propto\int\sqrt{\left(\frac{1}{\eta}-1\right) (d\eta)^2+(\eta d {\phi'}^2)}\\ =\int\sqrt{\left(\sqrt{\frac{1}{\eta}-1}d\eta\right)^2+\left(\sqrt{\frac{1}{\eta}-1}\eta d\phi'\right)^2}\]接著Transform Keplerian to SHO: (這個另外講軌跡的章節會再提到)
定
\[\eta\equiv\xi^2\]則
\[\int\sqrt{\left(\sqrt{\frac{1}{\eta}-1}d\eta\right)^2+\left(\sqrt{\frac{1}{\eta}-1}\eta d\phi'\right)^2}\\ =\int\sqrt{\left(\sqrt{\frac{1}{\xi^2}-1}2\xi d\xi\right)^2+\left(\sqrt{\frac{1}{\xi^2}-1}\xi^2d\phi'\right)^2}\\ =\int\sqrt{\left(2\sqrt{1-\xi^2}d\xi\right)^2+\left(\sqrt{1-\xi^2}\xi {d\phi'}^2\right)^2}\\ =2\int\sqrt{\left(\sqrt{1-\xi^2}d\xi\right)^2+\left(\sqrt{1-\xi^2}\xi \frac{d\phi'}{2}^2\right)^2}\]和前面SHO
\[\int\sqrt{(\sqrt{1-\zeta^2}d\zeta)^2+(\sqrt{1-\zeta^2}\zeta d\phi)^2}\]是同一個形式!只是變數替換一下
\[\zeta\equiv\xi,\quad \phi'=2\phi\\ \zeta^2=\eta, \quad \phi'=2\phi\]就是Bohhin transformation!(待補其他筆記)
繼續證明橢圓軌跡囉!
定
\[u\equiv\frac{1}{\eta}\]則
\[\begin{align*} &\int\sqrt{\left(\sqrt{\frac{1}{\eta}-1}d\eta\right)^2+\left(\sqrt{\frac{1}{\eta}-1}\eta d\phi'\right)^2}\\ =&\int\sqrt{(u-1)\left(d\frac{1}{u}\right)^2+(u-1)\frac{1}{u^2}(d\phi)^2}\\ =&\int\sqrt{\frac{u-1}{u^4}(du)^2+\frac{u-1}{u^2}(d\phi)^2}\\ =&\int\sqrt{\frac{u-1}{u^4}\dot{u}^2+\frac{u-1}{u^2}}d\phi,\qquad\dot{u}\equiv\diff{u}{\phi}\\ \equiv&\int L(u,\dot{u},\phi)\,d\phi \end{align*}\]這裡把$L(q,\dot{q},t)$換成$L(u,\dot{u},\phi)$,時間$t$的角色就是$\phi$。
記得我們最前面推導的過程,這個積分對應的就是
\[\begin{align*} &\delta\int\vv{p}\cdot d\vv{q}+tdH=0\\ =&\delta\int\sqrt{(2E-V(\vv{q}))d\vv{q}^t\cdot\hat{M}\cdot d\vv{q}}\\ =&\delta\int\sqrt{\frac{u-1}{u^4}\dot{u}^2+\frac{u-1}{u^2}}d\phi\qquad\dot{u}\equiv\diff{u}{\phi}\\ =&\delta\int L(u,\dot{u},\phi)\,d\phi=0 \end{align*}\]再來利用守恆的特性第十二節(記得有這樣的特性就是取完極值的結果)
\[\because \pdv{L}{\dot{q}}\dot{q}-L=\text{ an invariant of the motion when }\pdv{L}{t}=0\\ \therefore\pdv{L}{\phi}=0\Rightarrow \pdv{L}{\dot{u}}\dot{u}-L=c=\text{constant}\]所以算這個守恆量
\[\begin{align*} &\pdv{L}{\dot{u}}\dot{u}-L=c\\ =&\left(\frac{1}{\sqrt{\frac{u-1}{u^4}\dot{u}^2+\frac{u-1}{u^2}}}\frac{u-1}{u^4}\dot{u}\right)\dot{u}-\sqrt{\frac{u-1}{u^4}\dot{u}^2+\frac{u-1}{u^2}}\\ =&\frac{1}{\sqrt{\frac{u-1}{u^4}\dot{u}^2+\frac{u-1}{u^2}}}\left[\left(\frac{u-1}{u^4}\dot{u}^2+\frac{u-1}{u^2}\right)-\frac{u-1}{u^2}\right]-\sqrt{\frac{u-1}{u^4}\dot{u}^2+\frac{u-1}{u^2}}\\ =&-\frac{u-1}{u^2}\frac{1}{\sqrt{\frac{u-1}{u^4}\dot{u}^2+\frac{u-1}{u^2}}}\\ =&\frac{-\sqrt{u-1}}{u\sqrt{1+\frac{\dot{u}^2}{u^2}}}\\ \end{align*}\]移項
\[\Rightarrow u-1=c^2(u^2+\dot{u}^2)\\ \Rightarrow\dot{u}^2=\frac{u-1}{c^2}-u^2=-\left(u-\frac{1}{2c^2}\right)^2-\frac{1}{c^2}+\frac{1}{4c^4}\\ \Rightarrow\frac{du}{\sqrt{-\left(u-\frac{1}{2c^2}\right)^2-\frac{1}{c^2}+\frac{1}{4c^4}}}=d\phi\]令
\[\frac{u-\frac{1}{2c^2}}{\sqrt{-\frac{1}{c^2}+\frac{1}{4c^4}}}\equiv v\\ \Rightarrow \frac{dv}{\sqrt{1-v^2}}=d\phi\]設
\[v\equiv\sin\alpha\Rightarrow\alpha=\phi+\text{ some constant}\]符合上式。
接著
\[\because u\equiv\frac{1}{\eta}=\frac{1}{r}\]所以替換
\[\frac{1}{r}-\frac{1}{2c^2}=\sqrt{-\frac{1}{c^2}+\frac{1}{4c^4}}\sin(\phi+\text{ some constant})\]其中$\phi$+constant可以適當調整一下$\phi$ 起始點使得等於$\cos\phi$
\[\Rightarrow\frac{1}{r}=\frac{1}{2c^2}+\sqrt{-\frac{1}{c^2}+\frac{1}{4c^4}}\cos\phi\\ \Rightarrow r=\frac{2c^2}{1+e\cos\phi},\qquad e=\frac{\sqrt{-\frac{1}{c^2}+\frac{1}{4c^4}}}{\frac{1}{2c^2}}\]得證求變分,滿足Maupertuis’ Principle的條件後,可求守恆量對應的公式$r$,就是橢圓軌道!
(記得當時學到這裡的時候,心中滿滿的AMAZING!!太神奇了!)
例子二:克普勒正圓軌跡(momentum space)
別的筆記證明過,克普勒軌道在configuration space是橢圓,但在momentum space是正圓,現在用變分的方式重新去看這件事情。
變分公式用
\[\delta\int -\vv{q} d\vv{p}+tdH=0\]所以現在跟例子一有點不一樣,自由度在$p$,限制$q,t$,然後一樣滿足之前的條件
\[\begin{align*} &1. \quad H=\frac{\vv{p}^2}{2m}+V=E=\text{fixed alone varied trajectory}\\ &2. \quad \vv{q}\propto - d\vv{p} \end{align*}\]其中第二項來自於一樣之前對真實軌跡的導法
\[\diff{\vv{p}^*}{t^*}\propto -\hat{q}^*\]概念上也可以想像,因為現在是軌道,$\frac{dp}{dt}$就是向心力,即便$q$是varied過後的,一樣逃脫不了向心力的控制。
除此之外,位能表示為
\[V=-\frac{K}{\|\vv{q}\|}\]所以
\[\frac{\vv{p}^2}{2m}-E=-V=\frac{K}{\|\vv{q}\|}=\frac{\vv{p}^2}{2m}+|E|\\ \text{ (bound state orbit }E<0)\]再來因為我們要看momentum space,把$q$都變成$p$,另外因為兩者正比,所以內積就是直接乘
\[\int \vv{q}\cdot{d\vv{p}}=\int \|\vv{q}\| \|d\vv{p}\| = \int \frac{K\|d\vv{p}\|}{|E|+\frac{\vv{p}^2}{2m}}\\ \propto\int \sqrt{\frac{\|d\vv{p}\|^2}{(|E|+\frac{\vv{p}^2}{2m})^2}} =\sqrt{\frac{(dp)^2+p^2 d\phi^2}{(|E|+\frac{\vv{p}^2}{2m})^2}}\](這裡我們轉到極座標($p,\phi$)的momentum space比較好解)
所以
\[\int \vv{q}\cdot{d\vv{p}}=\sqrt{\left(\frac{1}{|E|+\frac{\vv{p}^2}{2m}}dp\right)^2+\left(\frac{1}{|E|+\frac{\vv{p}^2}{2m}}pd\phi\right)^2}\]跟前例一樣,rescale轉成在彎曲空間下無因次的測地線(geodetic)
\[\Rightarrow\text{factor }\int\sqrt{\left(\frac{d\rho}{1+\rho^2}\right)^2+\left(\frac{\rho}{1+\rho^2}d\phi\right)^2}\]變數變換一下,定
\[\rho\equiv\text{ dimensionless momentum}\equiv\tan{\beta}\\ \frac{\rho}{1+\rho^2}=\frac{\tan\beta}{1+\frac{\sin^2\beta}{\cos^2\beta}}=\tan\beta\cos^2\beta=\sin\beta\cos\beta=\frac{1}{2}\sin{2\beta}\\ \frac{d\rho}{1+\rho^2}=\frac{1}{1+\frac{\sin^2\beta}{\cos^2\beta}}\frac{1}{\cos^2\beta}d\beta=d\beta\]所以
\[\int\sqrt{\left(\frac{d\rho}{1+\rho^2}\right)^2+\left(\frac{\rho}{1+\rho^2}d\phi\right)^2}\\ =\int\sqrt{(d\beta)^2+\left(\frac{\sin 2\beta}{2}\right)^2d\phi^2}\\ =\frac{1}{4}\int\sqrt{d(2\beta)^2+(\sin 2\beta)^2(d\phi)^2}\]這個式子其實就是代表球面上線段(small line segment on a sphere)
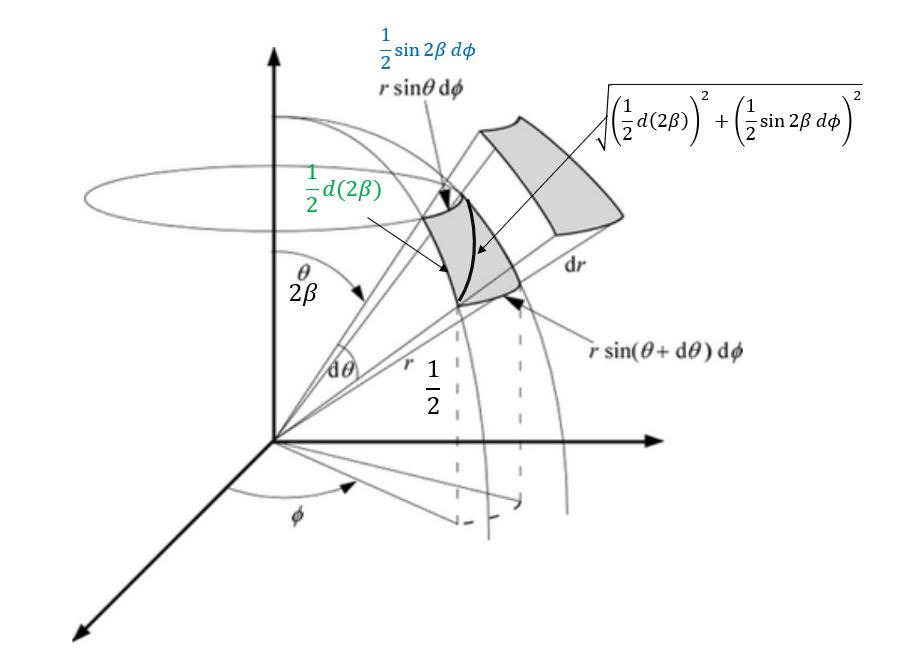
所以若是取這個線段積分的最小值
\[\delta\int -\vv{q} d\vv{p}+tdH=\delta\int -\vv{q} d\vv{p}\\ \Rightarrow\delta \frac{1}{4}\int\sqrt{d(2\beta)^2+(\sin 2\beta)^2(d\phi)^2}=0\]在球上其實就是大圓(最短距離)!
接下來我們回過頭來看$\rho$的意義,畫出來對應就是經過球極平面投影後,把這個大圓投影到momemtum plane上的直線!
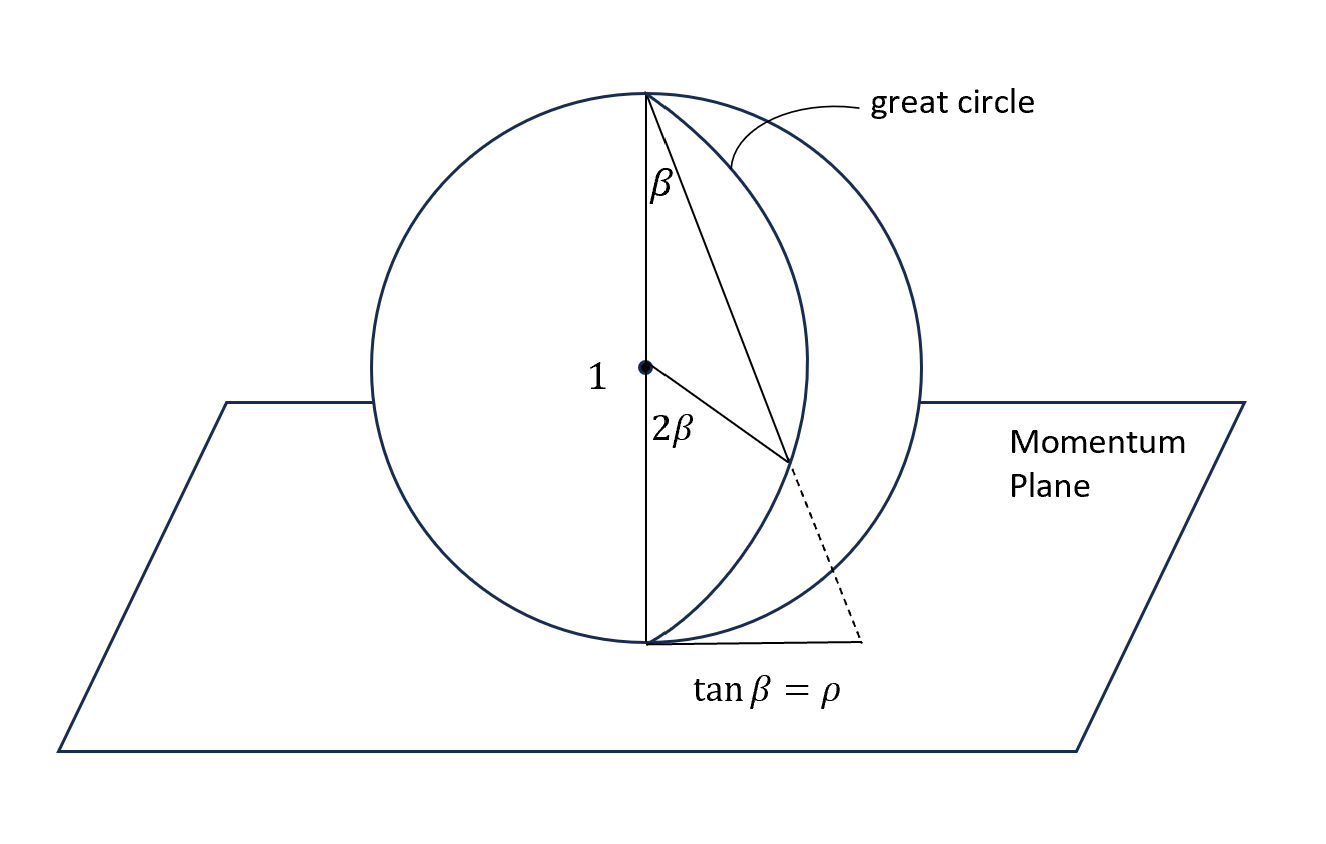
不過這個畫出來是比較特殊例子,因為剛好大圓取通過北極點,因此會是直線。
在更general的情況中,任何一個大圓經過球極平面投影都會投影成正圓,所以若我們取的大圓是通過球心的線段(不特別通過北極點),就可以得到這個例子最一開始想要證明的,克普勒軌道的true trajectory在momentum space上會是正圓。
以下畫個圖看一下,黑色是赤道圓,平面切割赤道面,紅色是任意大圓通過球心,綠線是北極點投影畫直線通過紅圈和平面,藍色就是在平面上的交點。
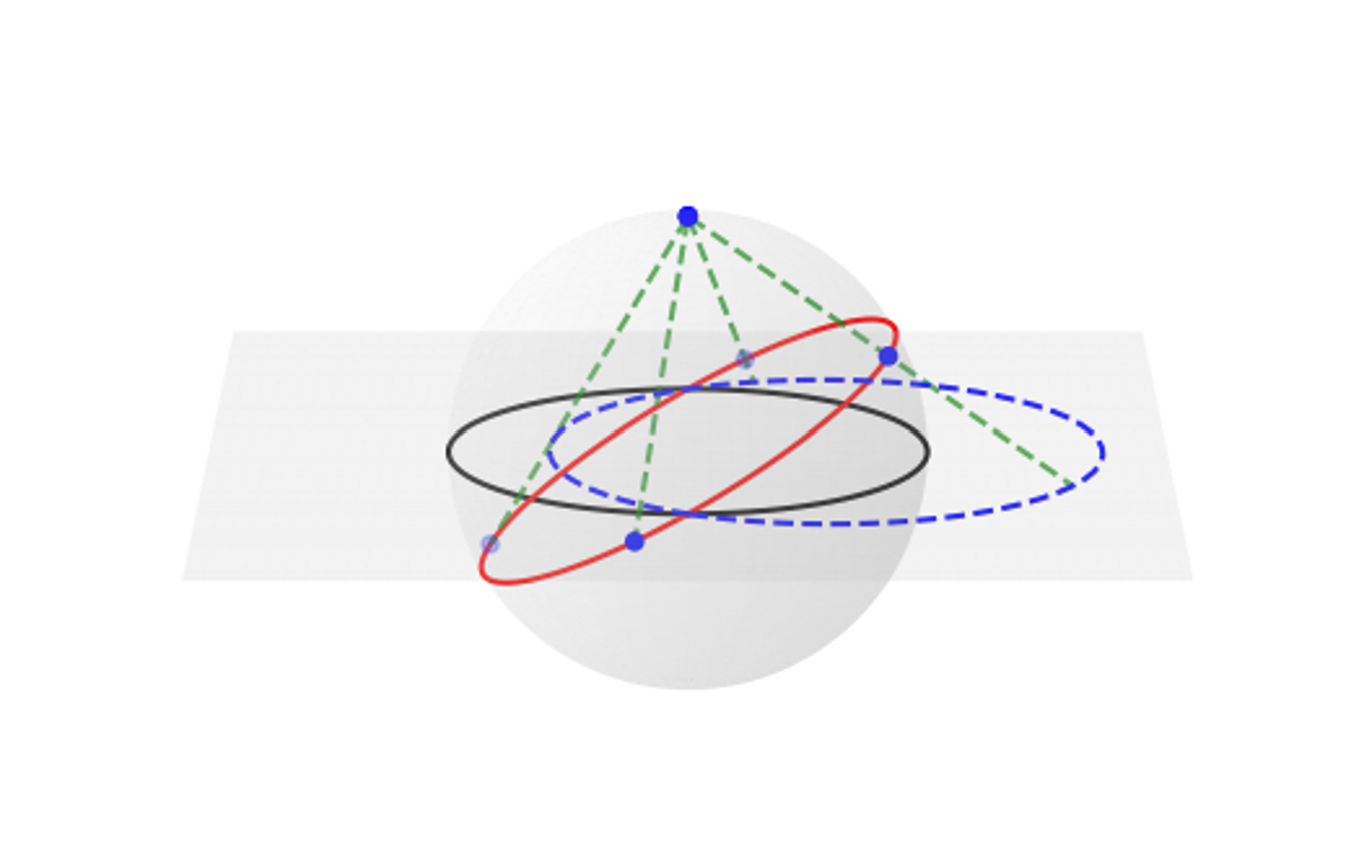
從俯視圖可以看得更清楚藍色是正圓!
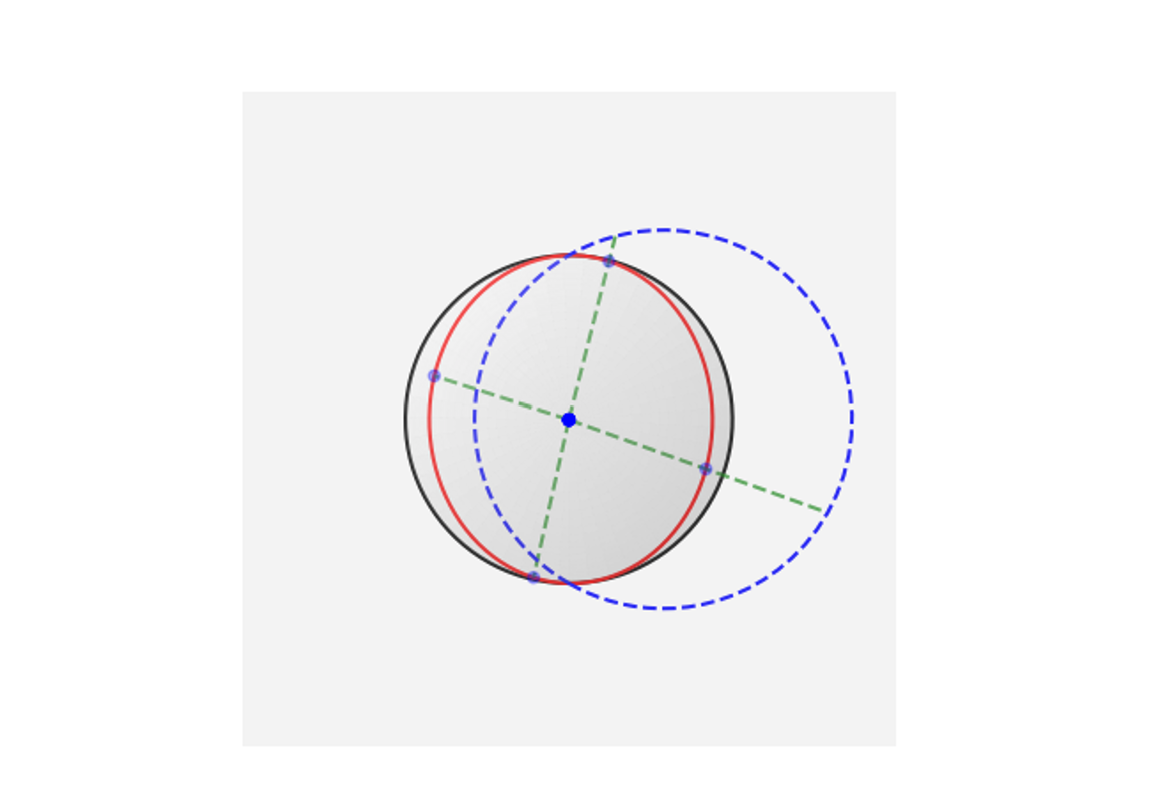
(Ref: https://graemewilkin.github.io/Geometry/Spherical_Geometry/Stereographic.html)
The shape of the true trajectory of the keplerian orbit in the “momentum plane” is simply the stereographic projection of a great circle(=a geodesic) on the spherical surface of radius 1/2.
Generally, one can show that a circle on the sphere is mapped to a circle on the plane under the stereographic projection.
Therefore, the trajectory in the momentum space are circles!
再論Maupertuis’ Principle
再複習一下,原本這個公式
\[\vv{p}=\hat{M}\cdot\diff{\vv{q}}{t}\]$q$可以自由選,$t$也可以自由調整,一旦$q,t$決定,$p$就會確定。
而Maupertuis’ Principle還有再加一個條件,就是$H$要固定
\[H=\frac{1}{2}\vv{p}^t\cdot\frac{1}{\hat{M}}\vv{p}+V=\text{constant}=E\]因此進一步限制了$t$,導致$t$沒有自由度,所以變成我們只有$q$可以自由選擇,但$p,t$都被限制住了。
只是我們為什麼要這麼做呢?
通常Hamiltoian equation of motion,是給定$q,p$之後,再去看下一個$q,p$,任意改,然後把整個trajectory解出來,是full variation,給我們最詳盡的解答。
但這裡因為被限制住了,所以只有partial variation,付出的代價就是只有得到partial information(用部分條件得部分資訊),如同前面舉的例子,只能得到橢圓(正圓)的軌跡,得到一個shape,但不會知道實際上是怎麼走的!不過對於有些問題,這樣得知shape其實就已經足夠。
就如同第十九節,用Hamiltonian算角動量的時候,也是用部份條件得部分資訊,但就足以證明角動量守恆。
最後再來一次用common的方式導出來
定我們的special system
\[H=\frac{1}{2}\vv{p}^t\cdot\frac{1}{\hat{M}}\cdot{\vv{p}}+V。\] \[\begin{align*} &\delta\int_{}^{}\vv{p}\cdot d\vv{q}=0\\ &=\delta\int \diff{\vv{q}^t}{t}\cdot\hat{M}\cdot d\vv{q}\\ &=\delta\int 2\cdot\frac{1}{2}\cdot\diff{\vv{q}^t}{t}\hat{M}\diff{\vv{q}}{t}\cdot{dt}\\ &=\delta\int 2(KE)\cdot dt\\ \end{align*}\]只要這個最小化求出來就能得到shape of true trajectory。
因此
\[\int_{}^{}\vv{p}\cdot d\vv{q}\]也稱為“action”(reduced action, or abbreviated action)。
不過公式中
\[\delta\int 2(KE)\cdot dt=0\]還是有時間項$dt$,但前面已說過我們現在不關心時間,對時間沒有興趣,只想看軌跡的形狀,$t$要被決定下來不能自己調
所以再繼續變換
\[\because \frac{1}{2}\cdot\diff{\vv{q}^t}{t}\hat{M}\diff{\vv{q}}{t}\cdot{dt}+V=E\Rightarrow\frac{\sqrt{2E-V}}{\sqrt{d\vv{q}\cdot\vv{M}\cdot d\vv{q}}}=\frac{1}{dt}\\ \therefore \delta\int 2(KE)\cdot dt = \delta\int\sqrt{(2E-V(\vv{q}))d\vv{q}^t\cdot\hat{M}\cdot d\vv{q}}=\delta\int\sqrt{\sum_{jk}^{}dq^j g_{jk}(\vv{q}) dq^k}=0\]就能得到代表最短的距離的Jacobi’s Form,
