(23) 變分 Adiabatic Invariant ─ 古典和量子的結合(軌道概念)
$J$和$E$的關係,比值是軌道週期
前兩個章節得出
\[J=\oint{pdq}=\frac{E}{\nu}=nh\]我們用圖來說明一下,進一步看$J$和$E$的關係。
當我們說對$J$做積分的時候,其實就是對這個periodic orbit(constant energy (E) curve)計算總面積,而從前面知道積分數值也是$nh$,代表n的取值越大,就是往外越大圈,面積越大。
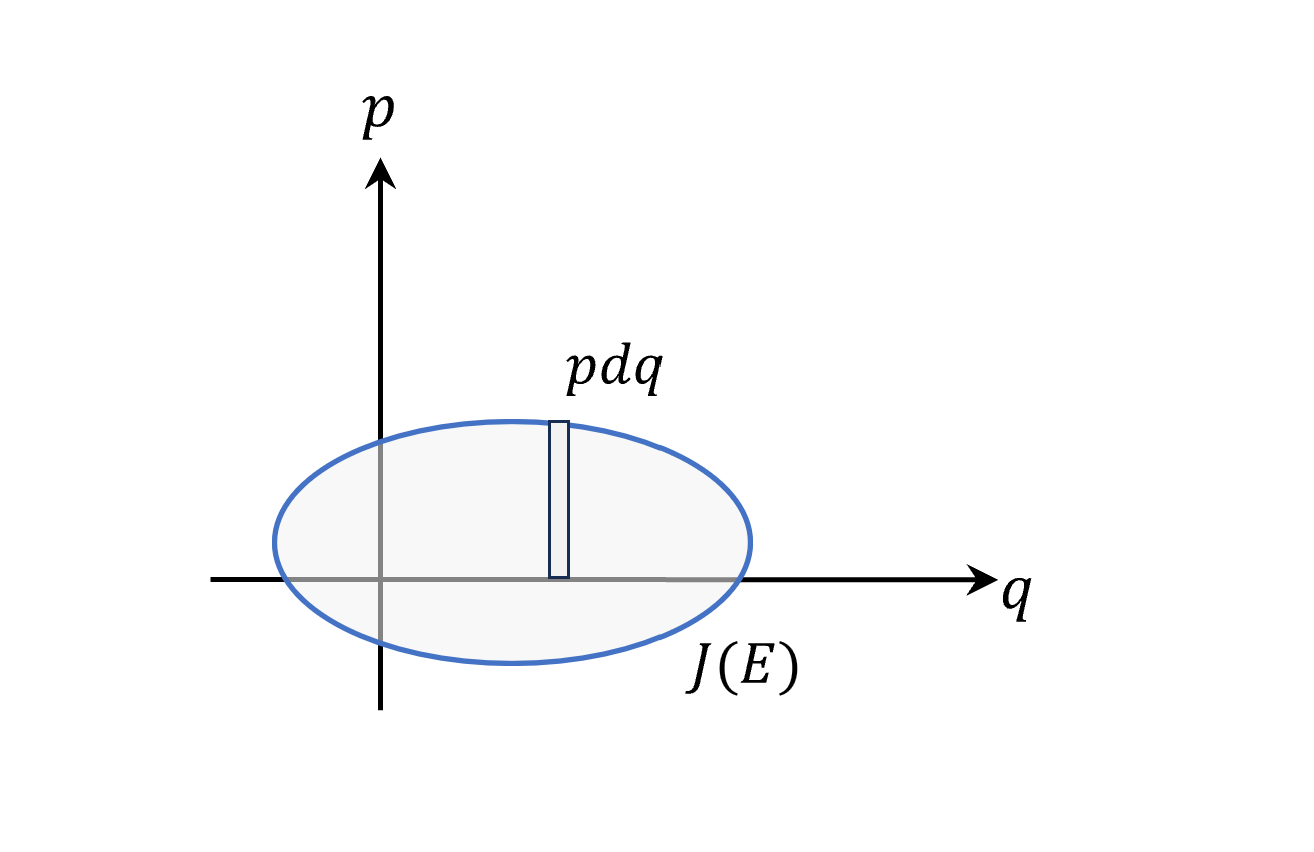
因此在phase space裡面積也是量子化的長大,但是為什麼大自然在phase space要做量子化,還不曉得原因。不過我們可以來算一下,假設現在有兩個periodic orbits(不同的E,也不一定要是橢圓或圓形),把外圈減內圈,算相差的面積。
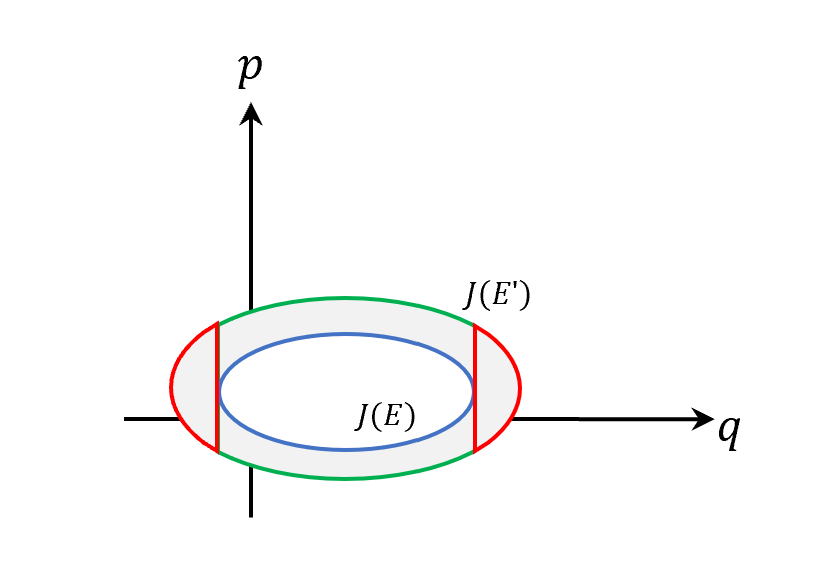
可以看到相差就是灰色的環狀面積,我們切成三個區域,左耳紅色、中環綠色、右耳紅色。
在等能量曲線上$H(q,p)=E$(能量給定),我們可以反函數得$p=p(q,E)$,所以
綠色區域
\[\begin{align} \text{green area}&\approx\oint\left({p(q,E')-p(q,E)}\right)dq\\ &\approx\oint\pdv{p(q,E)}{E}\Delta{E}dq=\mathcal{O}(\Delta E)\qquad\text{if $\Delta{E}$ is small} \end{align}\]紅色區域
\[\text{red ears}=\mathcal{O}(\Delta E^\frac{3}{2})\]先看左耳朵,左極端的內圈和外圈約相差$\Delta q$,其從Taylor知道$\propto\Delta E$,可以看成是二次曲線,橫軸上差$\Delta E$,縱軸上差$\sqrt{\Delta E}$,面積就差不多是$\Delta E\cdot\sqrt{\Delta E}=\Delta E^\frac{3}{2}$。
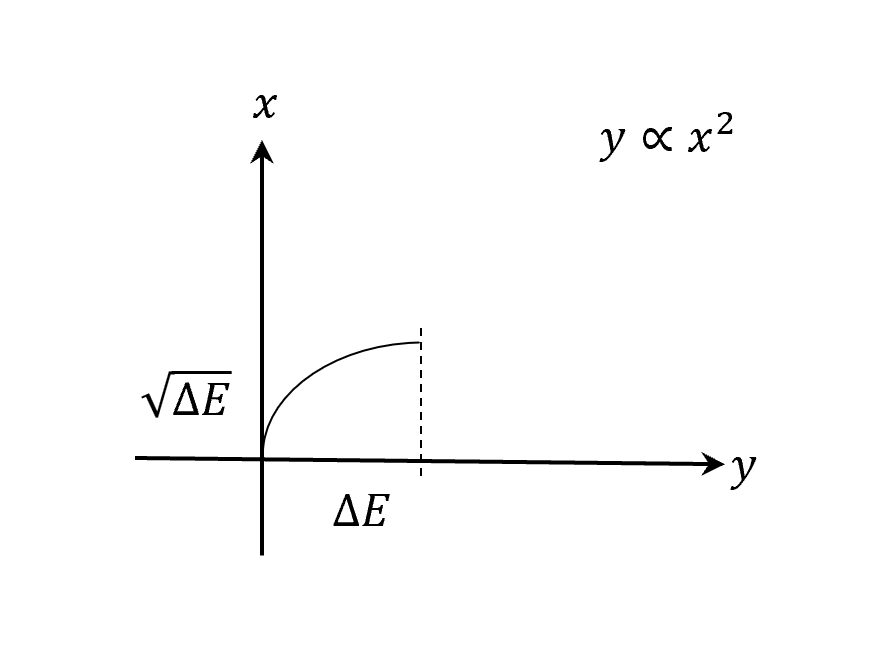
所以如果$\Delta E$,取很小的話,紅色區域就先不用管了。
來算 $\text{ Take limit }\Delta E \rightarrow 0$
\[\begin{align*} \diff{J}{E}=&\oint\pdv{p(q,E)}{E}dq\\ =&\oint\frac{1}{\frac{\partial{E}}{\partial{p(q,E)}}}dq\\ =&\oint{dt}\qquad\because\diff{q}{t}=\pdv{H(q,p)}{p}\text{ along the periodic orbit(trajectory)}\\ =&T(E)\equiv\text{ period of this periodic orbit}\\ \end{align*}\]我們得到一個驚人的結論
\[\Rightarrow\Delta{J}\approx T\Delta{E}\]代表當能量增加一點點,$J$也增大一點點,而這個增加的比值竟然就是軌道的週期!
結合量子力學
注意以上都還是單純古典力學的範疇,現在再來結合一下量力。
從上節我們知道Quantization Rule:
\[J(E_n)\stackrel{\text{(quantum)}}{=}nh\]古力告訴我們$J$差別和$E$的關係(這裡T(E)的E是某種平均的概念)
\[\therefore J(E_{n+1})-J(E_n)=h\stackrel{\text{(classical)}}{\approx}T(E)(E_{n+1}-E_n)\]所以振子的頻率關係可以寫成
\[\Delta{E}\approx\frac{h}{T}=h\nu_{\text{oscillation}}\quad\text{(by classical)}\]但我們又知道量力裡面,能階差就是放出光子的頻率
\[E_{n+1}-E_n=h\nu_{\text{emitting photon}}\quad\text{(by quantum for energy level jump)}\]所以得到重要的理解
\[\color{red}{\nu_{\text{photon}}=\nu_{\text{oscillation}}}\]代表我們現在處在一個灰色地帶
- 上式等號左邊是量子,需要薛丁格方程式來描述
- 上式等號右邊是古典,在我們做一堆近似之後結果
因此在做完這些近似,發現量子和古典竟然可以結合起來,同時具有兩邊過來的特性,我們稱為Semiclassical theory。
這個概念也含在Bohr’s Corresponding Principle
under suitable limits, the predictions of quantum theory should agree with those made by classical physics。
Bohr’s Semiclassical and Corresponding Principle
這裡我們再進一步來看重要的意義。
量子角度
不管古典不管軌道概念不管馬克士威,電磁波的頻率來自不同能階的跳躍,能階差/h就是觀察到的頻率。
古典角度
帶電粒子動來動去,我們就用馬克士威來解,解出來當初是用什麼頻率振它,它就放出什麼電磁波。
小結:量子世界軌道概念
從這裏的結合可以看到,量子世界裡面也可以有軌道的概念!
量子仍然可以和古典物理結合在一起,放出的光子和馬克士威預測的東西是一樣的,從兩邊看都是一樣的,就是semiclassical theory。
順帶一提,在波耳原子模型的時候,為什麼會定軌道角動量也是量子化的?為什麼不是其他的物理量或是做一些變化(取平方取log等等)? 在波耳原始論文裡面,認為有這些軌道,能階跳躍時會放出光子,放出能量,但波耳注意到你放出的這個光子頻率難道跟古典都沒有任何對應嗎?所以算一算如果for some reason,放出的頻率就是繞著軌道的頻率,所以他們軌道的頻率(certain average)和photon的頻率連在一起。然後他再回頭去看,energy level n,cicular orbit的角動量就是$n\hbar$,這個關聯就是Corresponding Principle。
