(24) 變分 Adiabatic Invariant ─ 用變分推導J和E的關係

上一章節我們從SHO EOM出發，得到$J$和$E$的關係，然後才繼續推出

\[\frac{\partial J}{\partial E}=T\]

現在我們單純用變分法再來證明一次這個關係，非常簡單！

變分法

採用extended phase space，選用積分公式

\[\int pdq+tdH\]

直接來畫圖，畫出真實和變分軌跡

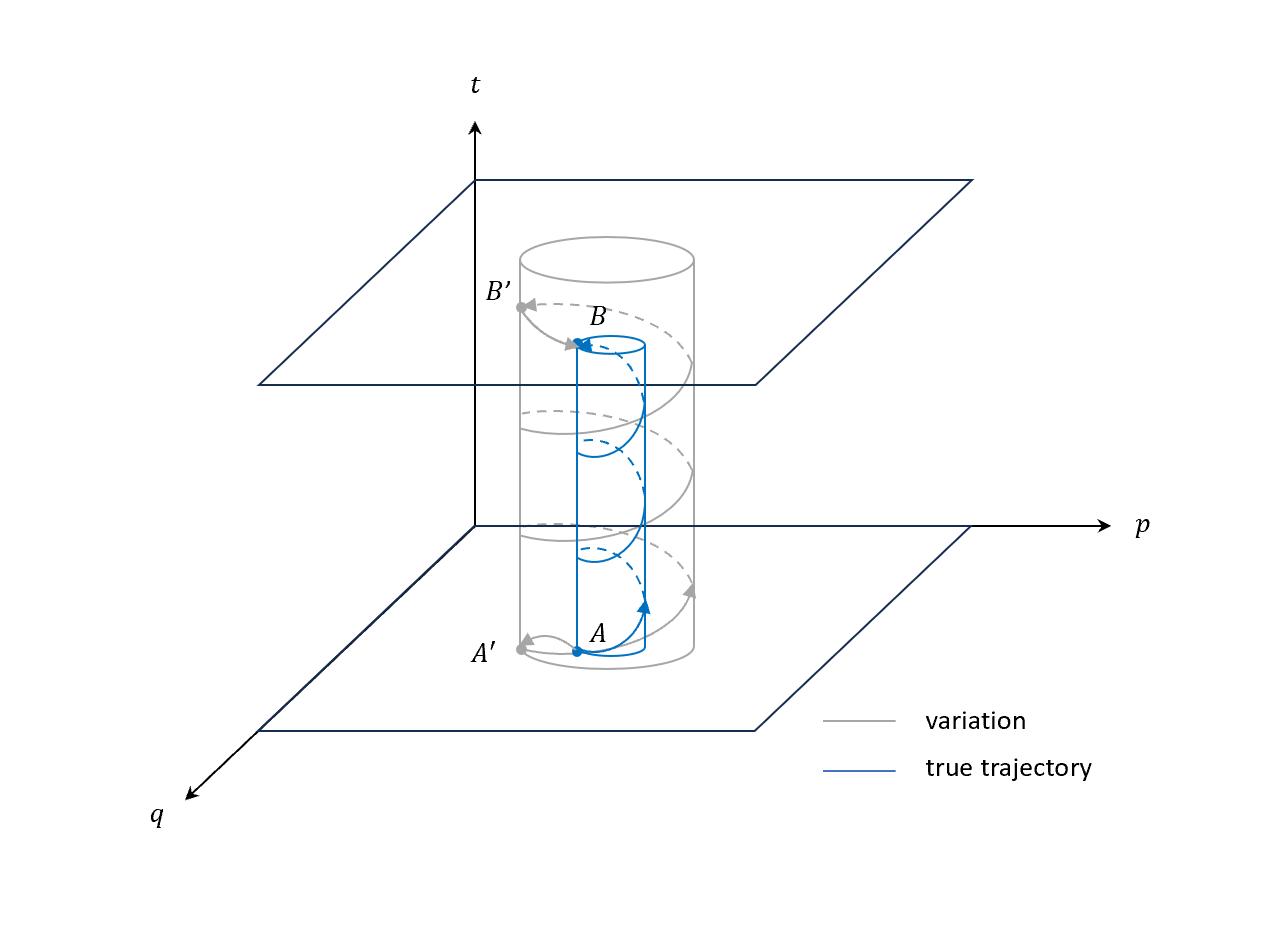
• 真實軌跡：$A \rightarrow B$
• 變分軌跡：$A \rightarrow A’ \rightarrow B’ \rightarrow B$

注意這個柱狀高度就是繞一圈週期軌道的週期時間。

真實和變分柱狀高度不用一樣，只有規定起始和終點的$q$要一樣，各自的$H$維持定值即可。

證明

接下來算差，一樣變分原則，我們近似到一階，所以

\[\int_\text{true trajectory} = \int_\text{varied trajectory}\] \[\Rightarrow J(E) + \int t dH = J(E') + \int t dH'\\ \because \text{同 cylinder 上繞的 } H \text{ 為定值 } (dH = 0)\\ \Rightarrow J(E) + 0 = J(E') + \int_{A \to A'} t dH + \int_{A' \to B'} t dH + \int_{B' \to B} t dH\]

• 右邊第二項：因為$t=0$所以消掉
• 右邊第三項：因為同柱，$dH$沒有改變消掉

所以

\[J(E) = J(E') + \int_{B' \to B} t dH\\ J(E') - J(E) \approx T(E' - E)\]

這樣就得證

\[\Rightarrow \frac{dJ}{dE} = T\]

簡單快速吧~