(25) 變分 Adiabatic Invariant ─ Action-Angle Variable

這是講 Adiabatic Invariant的最後一個小節，因為都是在講$J$，所以我就歸納在一起。

複習一下，在Phase space，我們知道封閉曲線的能量為定值，而$J$又是$E$的函式，所以在這個曲線上，任一點算的$J$數值也都是定值。

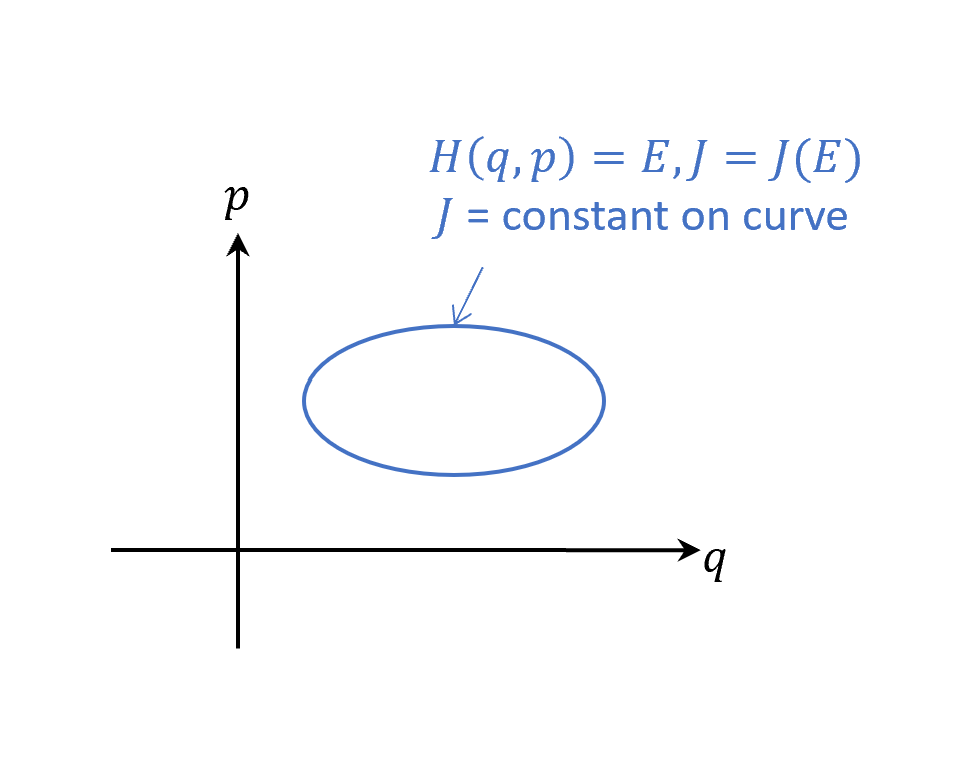
但是我們現在想要來做一個變數變換，使得

\[J(E)\rightarrow J(q,p)\]

這樣

\[J(q,p)\]

就也可以算是一種 canonical momentum，我們接著再類比於之前$H$的EOM定generalized coordinate $Q$。

變數變換

現在定$H$是新的$Q$和$J$的函數

\[H(Q,J)\]

按照之前邏輯

\[\left\{ \begin{array}{ll} \frac{dQ}{dt}=\frac{\partial H}{\partial J}\\ \frac{dJ}{dt}=-\frac{\partial H}{\partial Q} \end{array} \right.\]

第二條式子因為$J$是constant，所以等於零。

第一條則

\[\Rightarrow \frac{dQ}{dt}=\frac{\partial H}{\partial J}=\frac{1}{\frac{\partial J}{\partial H}}=\frac{1}{T(H)}\\ \Rightarrow Q=\frac{t}{T(H)}+constant\]

至此，我們稱$Q$為a sort of an angular variable。

(可以看到當$t$隨著時間變長到$T$(one periodic cycle)，$Q$第一項變成1，那就是繞一圈回來啦！)

Note:
如果看到教科書定義一圈是$2\pi$，格式就會長這樣 $$ J\equiv\frac{1}{2\pi}\oint pdq\\ \Rightarrow Q: 0\rightarrow 2\pi $$

為什麼我們要這樣做咧？

變換的好處

如果這是一個Hamiltonian可積分系統(Integrable System)，我們可以將其N自由度

\[(q_1, q_2, \dots, q_N, p_1, p_2, \dots , p_N)\]

做以上action-angle($J$-$Q$)的變數變換得

\[(J_k, \phi_k), \quad k=1,2,\dots,N\]

那就會非常方便了！

因為我們可以視為將整個系統拆分(decompose)出N個獨立的oscillating system，每個system都有自己的$(J,\phi)$，那就可以很好的進一步去做運算、解能量等等，

舉例

1. 2-D Keplerian System 我們可以拆分出兩個獨立震盪系統$r(t), \theta(t)$，譬如說知道$r$可以有遠近快慢，大小也有週期，我們就可以單獨看這個自由度(DOF)，了解其SHO等等。

2. 2-D SHO 我們可以簡單拆出$x(t), y(t)$的兩個獨立震盪系統。

網路上和書中都可以找到更多的例子，之後有機會再回來補實際的算法。