(26) 變分 Canonical Transformations
前言
現在要來求一件事情,當我們做變數變換之後,希望在extended phase space還能滿足Hamiltonian EOM的形式。
(想要做這個變換也是為了方便)
轉換成數學公式的意思就是
\[\text{Original: }(q,p,H)\rightarrow\text{New: }\left(Q(q,p,t), P(q,p,t), K(q,p,t)\right)\]並且仍然滿足以下三個公式
\[\left\{ \begin{array}{ll} \frac{d\vec{Q}}{dt}=\frac{\partial K}{\partial \vec{P}}\\ \frac{d\vec{P}}{dt}=-\frac{\partial K}{\partial \vec{Q}}\\ \delta\int\vec{P}d\vec{Q}-Kdt = 0 \end{array} \right.\]推導
先來看變分的部分,變數變換,代表兩者有對應關係,如以下圖示
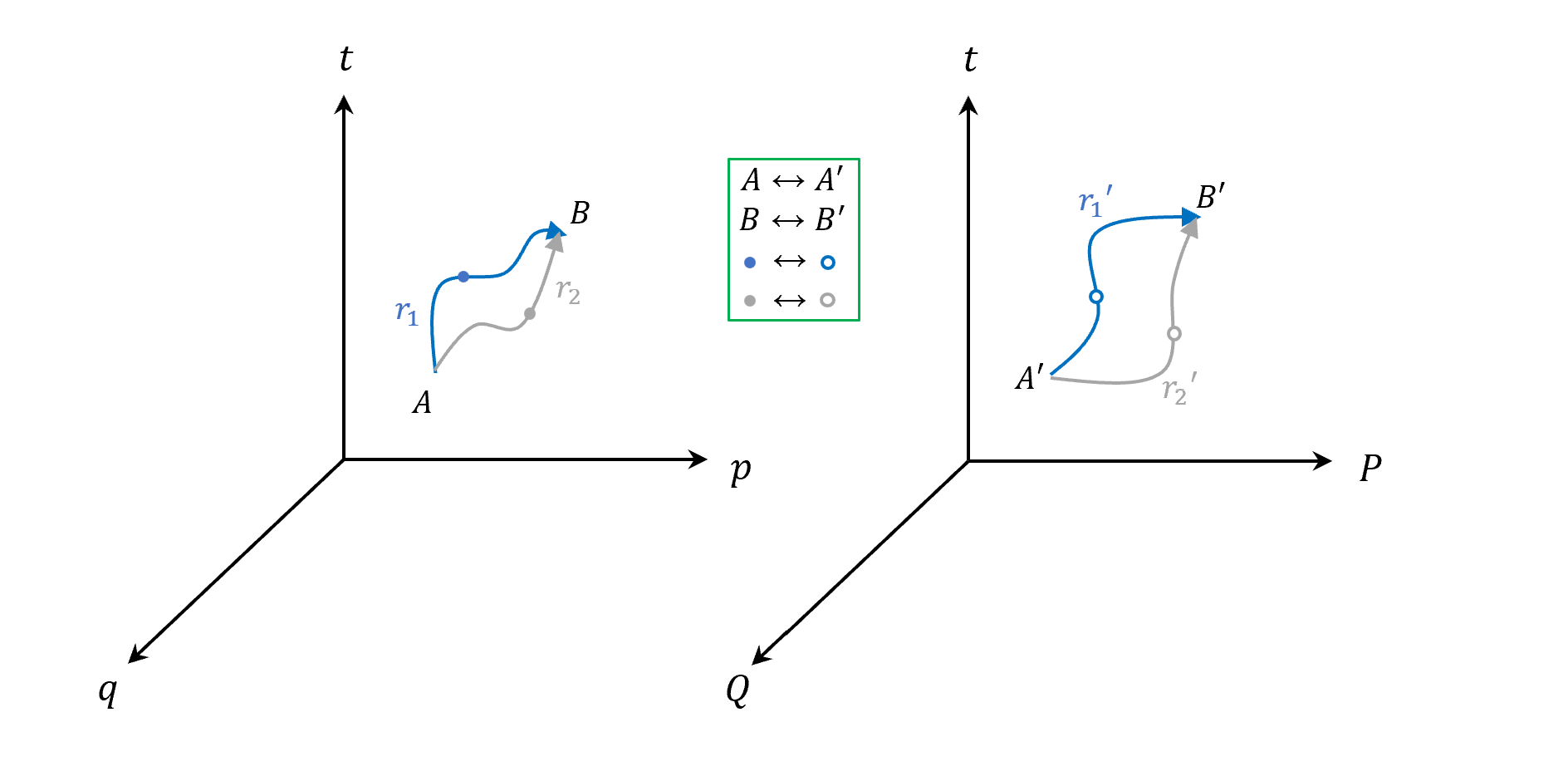
一樣算變分,各自space的改變的軌跡和真實軌跡相差都會是零,代表轉變前自己變分軌跡和真實軌跡的 差值 會和 轉變後自己變分軌跡及真實軌跡的差值 一樣!
我們用$\Delta$表示,所以兩邊相差都是零
\[\left(\int_{A_{r2}}^{B}-\int_{A_{r1}}^{B}\right)=\left(\int_{A'_{r2}}^{B'}-\int_{A'_{r1}}^{B'}\right)\\ \Rightarrow\Delta\left(\int \vec{p}d\vec{q}-Hdt\right)=\Delta\left(\int \vec{P}d\vec{Q}-Kdt\right)\\ \Rightarrow \Delta\int\left[( \vec{p}d\vec{q}-Hdt)-( \vec{P}d\vec{Q}-Kdt)\right]=0\]現在要做這個變數變換最初的初衷可能是為了方程式比較容易解,但不希望換了變數之後改變了原 本Hamiltonian EOM的性質。所以這個transformation並不是general,是特別的restrited case。
這裡回顧一下保守場的路徑積分
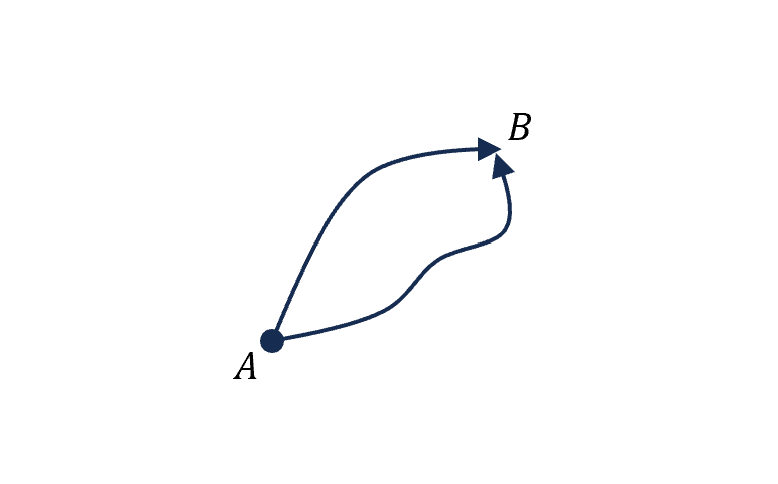
若這個式子要代表和路徑無關,就會有位能場的概念進來,寫成這樣
\[\vec{f}\cdot d\vec{r}=dF\\ \text{(for some }F=F(\vec{r}))\]把這個概念用到現在的轉換,因為我們這樣算軌跡的差,其實也代表我們不是很在乎到底 是哪條軌跡,所以把跟路徑無關的概念同樣導入進來
\[(\vec{p}d\vec{q}-Hdt)-( \vec{P}d\vec{Q}-Kdt)=dF\\ \text{(for some }F\text{ entended phase variables)}\]能寫成這樣就是Canonical transofmration definition。
移項一下
\[\begin{align} \vec{p}d\vec{q}-Hdt&=\vec{P}d\vec{Q}-Kdt+dF\\ &=d(\vec{P}\cdot\vec{Q})-\vec{Q}d\vec{P}-Kdt+dF\\ &=-\vec{Q}d\vec{P}-Kdt+dF_2, \quad F_2\equiv F+\vec{P}\cdot\vec{Q} \end{align}\]其實$F$或$F_2$都是generated function,不管是什麼型態,反正這個$F$都是自己定的。
例子一:求對應$\vec{Q}$的$\vec{P}$
假設我們現在要做的變數變換是
\[\vec{Q}\equiv\vec{f}(\vec{q},t)\]$\vec{f}$為已知,要找conjugate to $\vec{Q}$的$\vec{P}$。
方法一:從Generated Function $F_2$出發
(用Einstein’s summation convetion)
先改寫前面寫的
\[{p_j}d{q^j}-Hdt=-{Q^j}d{P_j}-Kdt+dF_2\\ \Rightarrow{p_j}d{q^j}+{Q^j}d{P_j}+(K-H)dt=dF_2\]我們知道
\[f\cdot d\vec{r}=dF(\vec{r})\Leftrightarrow \vec{f}=\frac{\partial F}{\partial \vec{r}}\]所以我們把$(q^j, P_j, t)$都視為在extended phase space的independent variables,$F_2$是$(q, P, t)$的函數。
類似地可以得到
\[\left\{ \begin{array}{ll} p_j=\frac{\partial F_2}{\partial q^j}\\ Q^j=\frac{\partial F_2}{\partial P_j}\\ K-H=\frac{\partial F_2}{\partial t} \end{array} \right.\]式子2:
從一開始的定義$\vec{Q}\equiv\vec{f}(\vec{q},t)$,我們知道
\[f^j(\vec{q},t)=\frac{\partial F_2(\vec{q}, \vec{P}, t)}{\partial P_j}\Bigg|_{q}\\ \Rightarrow F_2=f^{j'}(\vec{q},t)P_{j'}=\vec{f}\cdot\vec{P}\]代入式子3:
(記得$(q, P, t)$現在是independent variables)
\[K=H+\frac{\partial F_2}{\partial t}=H+\frac{\partial f^j(\vec{q},t)}{\partial t}P_j\]代入式子1:
\[p_j=\frac{\partial F_2}{\partial q^j}\Bigg|_{P}=\frac{\partial f^{j'} (\vec{q},t)}{\partial q^j}P_{j'}=\frac{\partial (\vec{f}\cdot\vec{P})}{\partial q}=\frac{\partial \vec{f}}{\partial q}\cdot\vec{P}\]最後得
\[P_{j'}=\frac{\partial q^j}{\partial f^{j'}}p_j\]方法二:從基本定義出發
一樣地開始假設
\[\vec{Q}\equiv\vec{f}(\vec{q},t)\]之前的關係式,所以$df$要變成全微分
\[\begin{align*} \vec{p}d\vec{q}-Hdt&=\vec{P}d\vec{Q}-Kdt+dF\\ &=P_{j'} df^{j'}-Kdt+dF\\ &=P_{j'}\left(\frac{\partial f^{j'}}{\partial q^j}dq^j+\frac{\partial f^{j'}}{\partial t}dt\right)-Kdt+dF \end{align*}\] \[\Rightarrow \left(p_j-P_{j'}\frac{\partial f^{j'}}{\partial q^j}\right)dq^j+\left(K-H-P_{j'}\frac{\partial f^{j'}}{\partial t}\right)dt=dF\]繼續來解,按照之前一樣的概念
\[\left\{ \begin{array}{ll} p_j-P_{j'}\frac{\partial f^{j'}}{\partial q^j}=\frac{\partial F}{\partial q^j}\\ 0=\frac{\partial F}{\partial P_j}\\ K-H-P_{j'}\frac{\partial f^{j'}}{\partial t}=\frac{\partial F}{\partial t} \end{array} \right.\]注意這裡沒有$dP$,所以$F$只是$(\vec{q},t)$的函式,跟$P$無關。
最後得
\[P_{j'}=\left(p_j-\frac{\partial F(\vec{q},t)}{\partial q^j}\right)\frac{\partial q^j}{\partial f^{j'}}\\ K=\frac{\partial F}{\partial t}+H+P_{j'}\frac{\partial f^{j'}}{\partial t}\]小結
$P$非unique
複習一下我們的初衷,是想要變換
\[(q,p,t) \rightarrow (Q, P, K)\]而這個例子中,已經給定
\[\vec{Q}\equiv\vec{f}(\vec{q},t)\]代表
\[q\leftrightarrow Q\]的關係有了,那會預期$p\leftrightarrow P$也會有一個獨立的對應形式,但從前面方法求出來的
\[P_{j'}=\left(p_j-\frac{\partial F(\vec{q},t)}{\partial q^j}\right)\frac{\partial q^j}{\partial f^{j'}}\]看到$P$必須取決自$F$的選擇,$F$只是$(\vec{q},t)$的函式,跟$P$無關,但任意選擇的結果,會影響最後$P$的結果,與我們預期的”有獨立對應形式”的結果完全不同。
如果無關時間,可視$K=H$
如果我們一開始取的
\[\vec{f}=\vec{f}(\vec{q})\]和$t$無關,則
\[K-H=\frac{\partial F}{\partial t}\]竟然$K$和$H$都是常數,$F$也會和$t$無關,那我們乾脆讓生活簡單一點,直接代
\[K=H\]就好哩!(注意要直接代,必須要滿足這些條件,不然直接K=H是錯的!)
例子二:$P$非unique
現在做簡單一點的座標轉換,設
\[\vec{Q}\equiv \vec{f}(\vec{q})\equiv \vec{q}\] \[\frac{\partial f^{j'}}{\partial q^j}=\delta_{j}^{j'}\] \[\delta_{j}^{j'}\equiv \left\{ \begin{array}{ll} 1 \text{ if }j'=j\\ 0 \text{ otherwise} \end{array} \right.\]一樣,我們會覺得這裡$Q\leftrightarrow q$都直接代了,那$P\leftrightarrow p$也應該就直接代吧!
是這樣嗎?我們來算。
套用前面做法
\[\left\{ \begin{array}{ll} p_j-P_{j'}\frac{\partial f^{j'}}{\partial q^j}=p_j-P_j=\frac{\partial F}{\partial q^j}\\ K=H-P_{j'}\frac{\partial f^{j'}}{\partial t}=H \end{array} \right.\] \[\Rightarrow p_j=P_j+\frac{\partial F}{\partial q^j}=P_j+\frac{\partial F(\vec{Q})}{\partial Q^j}\]看這個式子還是很抽象對吧,沒關係,我們來舉一般3D的例子。
一般3D轉換例子
熟悉地
\[H(q,p)=\frac{\vec{p}^2}{2m}+V(\vec{q})\\ \vec{q}\text{: ordinary Euclidean coordinate}\\\]我們定
\[\vec{q}\equiv\vec{r}\]轉換到$(\vec{Q}, \vec{P}, K)$
\[K(\vec{Q}, \vec{P})=\frac{\left(\vec{P}+\frac{\partial F}{\partial Q}\right)^2}{2m}+V(\vec{Q})\\ =\frac{\left(\vec{P}+\frac{\partial F}{\partial r}\right)^2}{2m}+V(\vec{r})\\ =\frac{\left(\vec{P}+\nabla F\right)^2}{2m}+V(\vec{r})\]可以看到
\[\vec{P}+\nabla F\]就和熟知的momentum(mv)不一樣了,$F$的選擇也會影響此項,所以這個momentum不會是unique。
但是呀!記得我們現在只是做座標轉換,雖然不是unique,物理還是一樣的物理。
更Generalized的例子:磁場中的帶電粒子
這次更Generalized一點,不一定非得是$\nabla F$的形式:
\[H=\frac{\left(\vec{P}+\vec{a}\right)^2}{2m}+V(\vec{r})\\ \nabla \times \vec{a}\neq 0\]就像是在磁場中的帶電粒子,設$\vec{A}$為vector potential
\[H=\frac{\left(\vec{P}-\rho\vec{A}\right)^2}{2m}+V(\vec{r})\]Generalized EOM
\[m\frac{d^2\vec{r}}{dt^2}=-\nabla V +\frac{d\vec{r}}{dt}\times(-\nabla\times\vec{a})\]看等號右邊第二項,這是一個和速度垂直的力!
這裡重要的意義在於,在generalize後,可以求出一個看起來和速度垂直的力(後見之明:勞倫茲力),但在19世紀初,這件事情是很amazing的,因為只看到有某個未知的作用力和速度垂直,是 後來的電磁學才有發現和證明出這個磁場作用力。
這樣的概念可以沿用到場論,有時候是為了想確立某個特性(e.g., symmetry),推導的時候少了一些component,所以引入spin的概念,加了 一些compoenent近來,而後來實驗證明的實際情況也是對的。
所以有時候在做物理,我們可以推導出來之後再往generalization的方向進一步推導,但當然還是 要看實際情況,不會每次都成功,但當能夠generalize之後,視野可以從更高的格局去看問題, 就能發現更多有趣的現象,把一些東西都可以歸納進來!
例子三:把$p$當作$Q$,地位變換後也是一樣的
現在定
\[\vec{Q}\equiv\vec{p}\]一樣,前面的式子變成
\[\begin{align} \vec{p}d\vec{q}-Hdt&=\vec{P}d\vec{Q}-Kdt+dF\\ &=\vec{P}d\vec{p}-Kdt+dF \end{align}\] \[\Rightarrow \vec{p}\cdot d\vec{q}-\vec{P}\cdot d\vec{p}+(K-H)dt=dF\]跟以往不同的是,現在是$F$是三個變數的函式囉!
\[F\equiv F(\vec{q},\vec{p},t)\]所以列出來
\[\left\{ \begin{array}{ll} \vec{p}=\frac{\partial F(\vec{q},\vec{p},t)}{\partial \vec{q}}\\ -\vec{P}=\frac{\partial F}{\partial \vec{p}}\\ K-H=\frac{\partial F}{\partial t} \end{array} \right.\]式子一
\[F=\vec{p}\cdot{\vec{q}}\]式子二
\[-\vec{P}=\frac{\partial (\vec{p}\cdot{\vec{q}}) }{\partial \vec{p}}=\vec{q}\]式子三
\[K=H\]
但其實這樣的結果本來就會知道,因為從原本出發,就是$p,q$對調加負號
1.原本H EOM
\[\left\{ \begin{array}{ll} \frac{d\vec{q}}{dt}=\frac{\partial H(\vec{q},\vec{p},t)}{\partial \vec{p}}\\ \frac{d\vec{p}}{dt}=-\frac{\partial H}{\partial \vec{q}} \end{array} \right.\]2.現在假設$\vec{Q}\equiv\vec{p}$
\[\left\{ \begin{array}{ll} \frac{d\vec{q}}{dt}=\frac{\partial H(\vec{q},\vec{Q},t)}{\partial \vec{Q}}\\ \frac{d\vec{Q}}{dt}=-\frac{\partial H}{\partial \vec{q}} \end{array} \right.\]3.然後從微分方程式知道$\vec{P}=-\vec{q}$
\[\left\{ \begin{array}{ll} -\frac{d\vec{p}}{dt}=\frac{\partial H}{\partial \vec{Q}}=\frac{\partial K}{\partial \vec{Q}}\\ \frac{d\vec{Q}}{dt}=\frac{\partial H}{\partial \vec{P}}=\frac{\partial K}{\partial \vec{P}} \end{array} \right.\]可以看到1和3其實是一樣的(只是差負號),$q,p$地位仍然一樣。
