(27) 變分 Hamiltonian-Jacobi Theory ─ 得到真實軌跡?
前言
這是變分裡最後一個主題,Hamiltonian-Jacobi Theory。
我們從一開始就一直強調變分的概念,現在再回頭來看變分的這個action物理量。
之前的概念是,給定初始和終止條件,兩個endpoint,算action的積分,取極值後就能得到true trajectory。
\[\delta\int \vec{p}\cdot d\vec{q}-Hdt=0\]其中我們通常定
\[(q^*, p^*)\]為真實軌跡,初始和結束條件$(\vec{q}_0,t_0), (\vec{q}_f,t_f)$。
現在我們額外定一個新的變數
\[S^*(\vec{q}_0,t_0,\vec{q}_f,t_f)\equiv \int \vec{p}^*\cdot d\vec{q}^*-H^*dt\\ \text{(evaluated along the true trajectory)}\\ S(\vec{q}_0,t_0,\vec{q}_f,t_f)\equiv \int \vec{p}\cdot d\vec{q}-Hdt\\ \text{(any trajectory connecting }(\vec{q_0},t_0)\to(\vec{q_f},t_f))\]而最後這個章節我們要探討的,就是${S^* }$怎麼隨著$\vec{q}_0,t_0,\vec{q}_f,t_f $改變而變化。
討論參數改變
$q$改變
現在我們只改變$q_f$
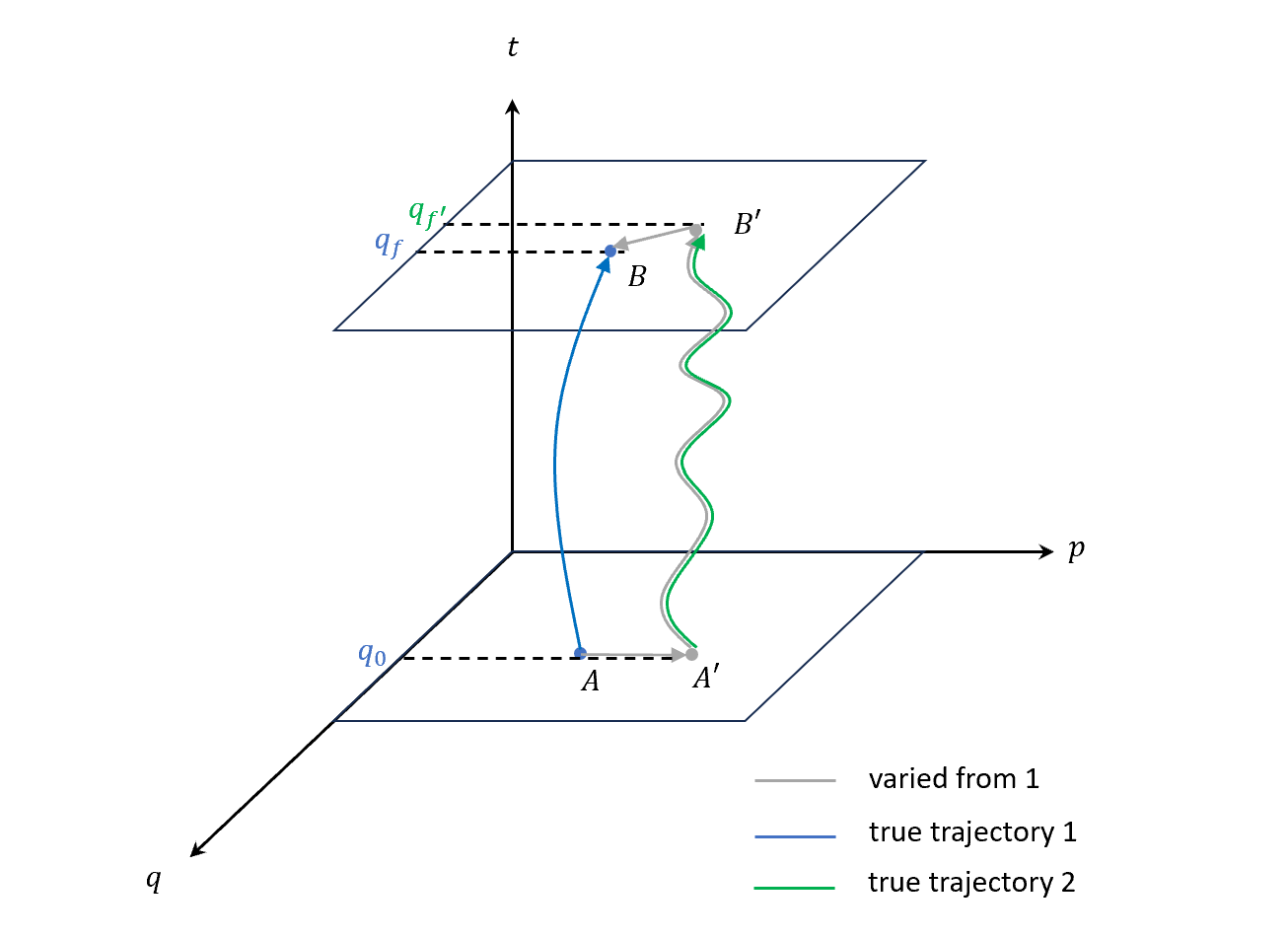
(可以想像起始點都是地球,終點是月球,但一個在月球的$B$點,一個在$B’$點,想必射出去軌跡一定不一樣,起始速度也會不一樣,因此對應藍色真實軌跡是到$B$、綠色真實軌跡是到$B’$,$q_0$同,但$p$不同。)
一樣做變分,灰色軌跡是對藍色真實軌跡的變分
\[\int_{A\to A'\to B'\to B\text{ (varied)}} pdq-Hdt=\int_{A\to B \text{ (true)}} pdq-Hdt\]拆解出每一段
\[\int_{A\to A'\to B'\to B}=\int_{A\to A'}+\int_{A'\to B'}+\int_{B'\to B}=\int_{A\to B}\]第一段
因為$q_0$和$t_0$相同,積分起來就消掉了。
\[\int_{A\to A'}=0\]第二段
用綠色的真實軌跡表示為
\[S^{*}(\vec{q}_0,t_0,\vec{q}_{f'},t_f)\]第三段
$q_f$不同,$t_f$相同
\[\int_{B'\to B}=p_f(q_f\big|_B-q_f\big|_{B'})=-p_f\cdot\Delta q_f, \quad\Delta q_f\equiv q_{f'}-q_f\]整合起來得
\[S^{*}(\vec{q}_0,t_0,\vec{q}_{f'},t_f)-S^{*}(\vec{q}_0,t_0,\vec{q}_{f},t_f)=p_f\Delta q_f\\ \Rightarrow p_f=\frac{\partial S^*}{\partial q_f}\]$t$改變
現在我們只改變$t_f$
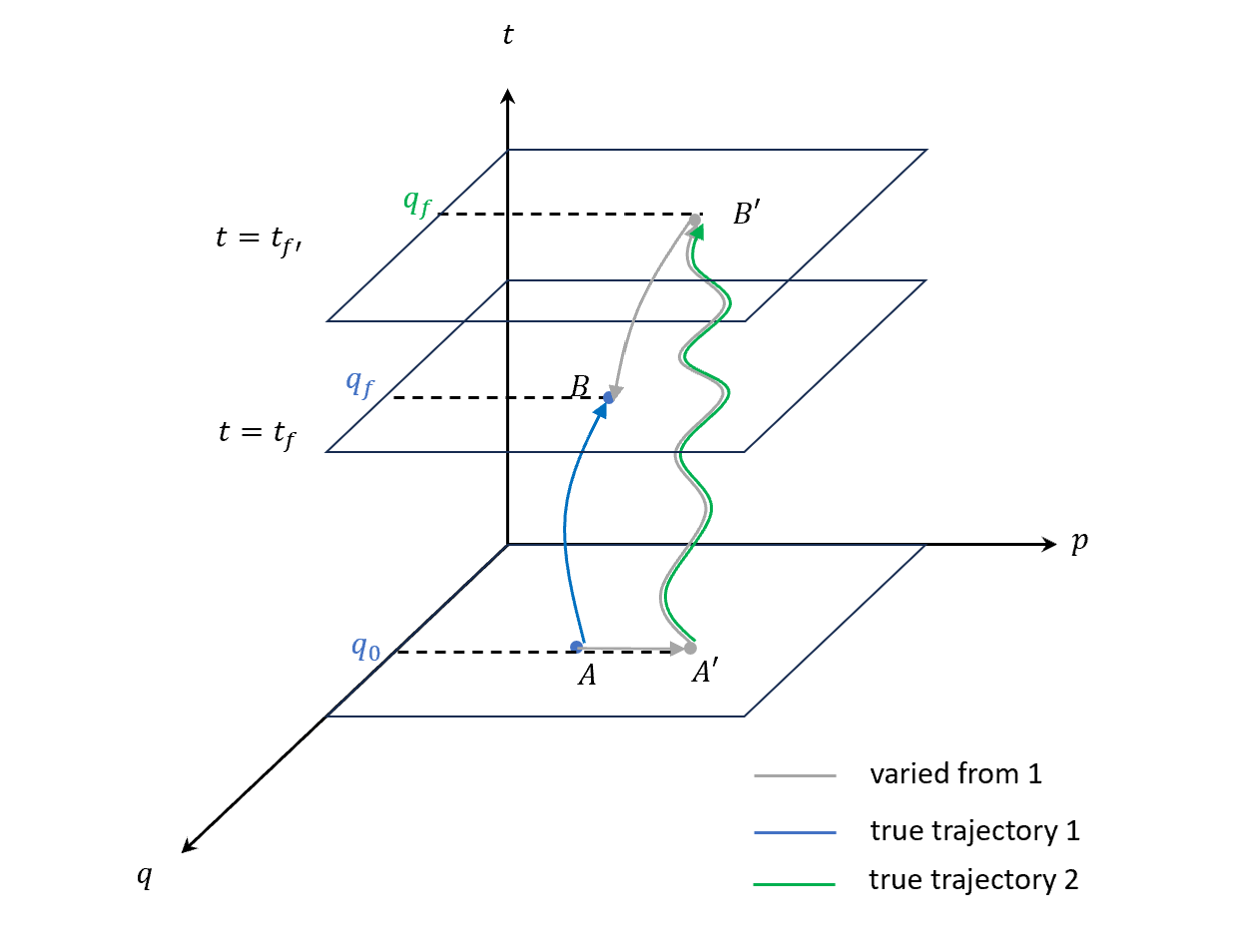
跟前面一樣,拆成三段
\[\int_{A\to A'\to B'\to B}=\int_{A\to A'}+\int_{A'\to B'}+\int_{B'\to B}=\int_{A\to B}\]第一段
因為$q_0$和$t_0$相同,積分起來就消掉了。
\[\int_{A\to A'}=0\]第二段
用綠色的真實軌跡表示為
\[S^{*}(\vec{q}_0,t_0,\vec{q}_{f},t_{f'})\]第三段
$t_f$不同,$q_f$相同
\[\int_{B'\to B}=H_f(t_f\big|_B-t_f\big|_{B'})=-H\cdot\Delta t_f, \quad\Delta t_f\equiv t_{f'}-t_f\]整理得
\[-H_f=\frac{\partial S^*}{\partial t_f}\]整理
其他兩個同理,可以整理得到
\[\left\{ \begin{array}{ll} p_0=-\frac{\partial S^*}{\partial q_0}\\ H_0=\frac{\partial S^*}{\partial t_0} \end{array} \right.\] \[\left\{ \begin{array}{ll} p_f=\frac{\partial S^*}{\partial q_f}\\ H_f=-\frac{\partial S^*}{\partial t_f} \end{array} \right.\]意義解釋
綜合以上,如果我們知道某個真實軌跡的函式形式(functional form)
\[S^*(q_0,t_0,q_f,t_f)\]也已知其中一條關係式
\[p_0=-\frac{\partial S^*(q_0,t_0,q_f,t_f)}{\partial q_0}\]等於我們知道了$p_0$和$(q_0,t_0,q_f,t_f)$的關係,可以反推求得
\[q_f=q_f(q_0,\color{red}{p_0},t_0,t_f)\]舉例已知真實軌跡
假設我們知道
\[S^*=\sin(q_0^2\cdot t_0\cdot t_fe^{q_f})\]則
\[p_0=-\frac{\partial S^*(q_0,t_0,q_f,t_f)}{\partial q_0}=-2q_0\cos(q_0^2 t_0 t_fe^{q_f})(t_0 t_fe^{q_f})\]若$q_0, t_0$已知,則可以改寫而得
time evolution of $q_{f}(t)$:
\[q_f=q_f(t_0,t_f,q_0,p_0)\]
同理,$p_f$可以繼續透過
得到time evolution of $p_{f}(t)$!
我們到底在幹嘛
所以咧?講到這邊我們到底在幹嘛?
我們先
- 假設已知$S^{*}, q_0, t_0$。
- 用initial condition 得到$q_f(t)$隨時間演變的函數形式。
- 得到$q_f$之後,繼續推得$p_f(t)$隨時間演變的函數形式。
然後我們就能解系統了!
但這根本是廢話!
你看看我們第一個的大前提,是真實軌跡$S^{*}$已經知道,那這不是無聊嘛!若我們能知道真實軌跡,本來想要求什麼問題都沒問題。
場論
所以接下來,我們其實要用一個旁門左道的辦法,沒有真的要去求真實軌跡,但還是必須得到$S^*$的函數形式,這個方法用到場論(field theory),就是最後這個章節要講到的
Hamiltonian-Jacobi Theory。
注意場論其實就是在解特定的position和time,把wave和particle trajectory結合在一起去解,更進一步地說,我們在這裡處於middle,在場論的世界中,把量子和古典做結合,用更完整的角度去看這些事情。
