Cjue25

Good things take time

前言

上一節說到，當我們知道真實軌跡

\[S^*(q_0,t_0,q_f,t_f)=\int p dq-Hdt\]

就可以知道系統的完全動態

\[\left\{ \begin{array}{ll} p_0=-\frac{\partial S^*}{\partial q_0}\\ H_0=\frac{\partial S^*}{\partial t_0}\\ p_f=\frac{\partial S^*}{\partial q_f}\\ H_f=-\frac{\partial S^*}{\partial t_f} \end{array} \right.\]

其中因為

\[p_0=-\frac{\partial S^* (q_f, q_0, t_f, t_0)}{\partial q_0}\]

再藉由$p_0$反推

\[q_f=q_f(q_0,p_0,t_0,t_f)\]

這樣只要知道 inital condition $(q_0, t_0)$，就能推得$q_f(t_f)$和$p_f$。

Canonical Transformation

算

\[dS^*(q_f,q_0,t_f,t_0) = \frac{\partial S^*}{\partial q_f} dq_f+\frac{\partial S^*}{\partial q_0} dq_0+\frac{\partial S^*}{\partial t_f} dt_f + \frac{\partial S^*}{\partial t_0} dt_0\]

則可知 Identity (代進去等號左右相等)

\[p_fdq_f-H_fdt_f=p_0dq_0-H_0dt_0+dS^*\]

對照第二十六節學的

\[\vec{p}d\vec{q}-Hdt=\vec{P}d\vec{Q}-Kdt+dF\]

把$dS^*$想成$dF$，不就是Canonical Transformation嗎！

所以我們可以把起始點$(q_0,p_0,t_0)$到終點$(q_f,p_f,t_f)$想成是座標轉換，兩者都視作在extended space coordinate，當然我們也可以反過來想，不論是幾秒之後發生的座標，都可以轉回成initial condition的樣子。

變分

那就一樣來做變分吧！以下藍色是真實軌跡，灰色是變分軌跡，從起始點到終點，注意一般來說，不一定非要$t=0$或是$t=\text{fixed}$的平面。

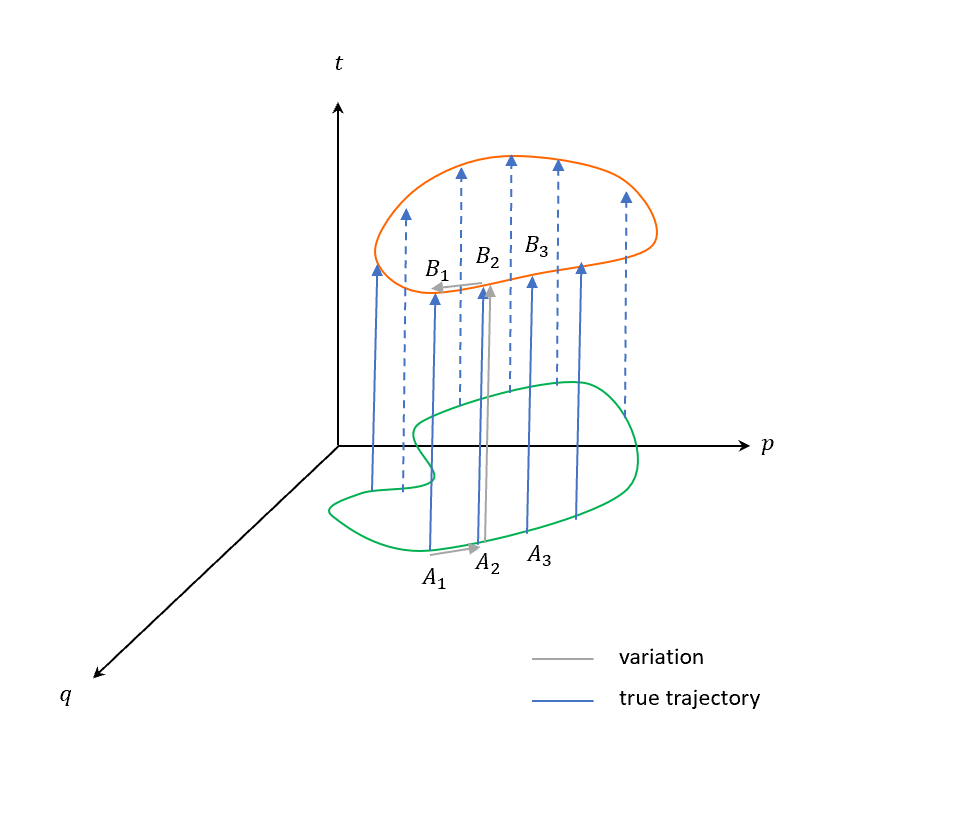
拆解成三個分段做變分

\[\int_{A_1\to B_1} (pdq-Hdt)=\int_{A_1\to A_2}+\int_{A_2\to B_2}+\int_{B_2\to B_1}\]

這樣就相當於，繞一圈的路徑積分是0！

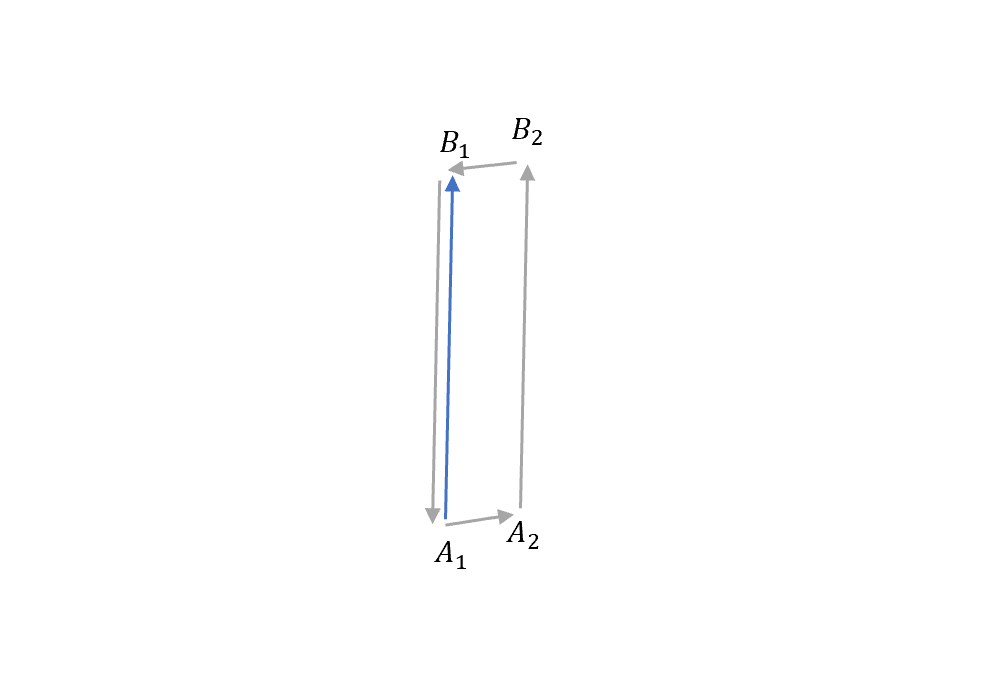
\[\int_{A_1\to B_1}=\int_{A_1\to A_2 \to B_2 \to B_1}\\ -\int_{A_1\to B_1}+\int_{A_1\to A_2 \to B_2 \to B_1}=0\\ \int_{A_1\to A_2 \to B_2 \to B_1 \to A_1}=0\]

所以我們可以把第一張圖切成很多一圈一圈的路徑，每一圈都是0，全部積完也是0！

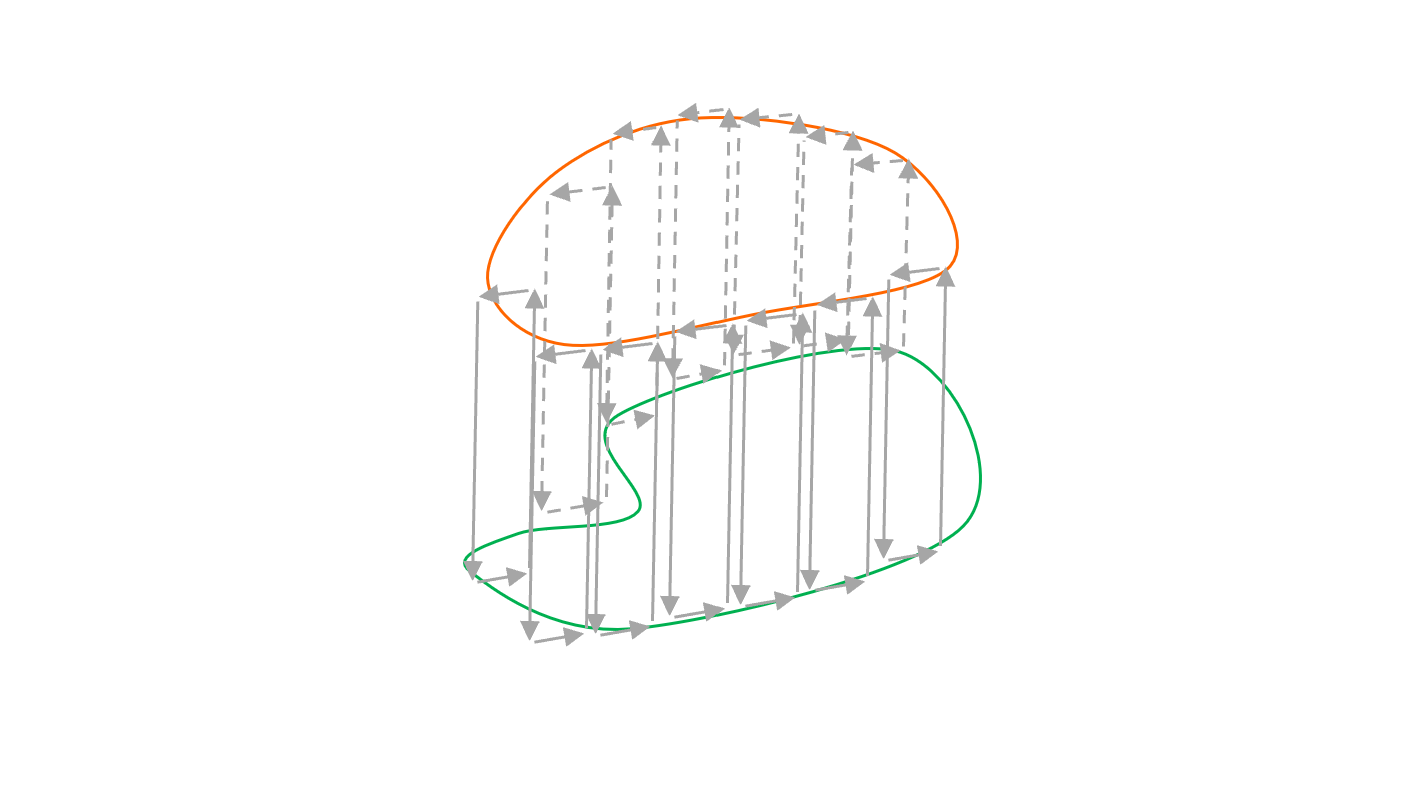
然後積分過程中，因為長條邊會相消，所以可以得出橘圈加綠圈等於0。

\[\int_{B_1\to B_2 \to B_3 \to B_1} pdq-Hdt = \int_{A_1\to A_2 \to A_3 \to A_1} pdq-Hdt\\ \oint_{\text{green circle}}p_0 dq_0-H_0 dt_0=\oint_{\text{orange circle}}p_f dq_f-H_f dt_f\]

(不過這也本來就是Canonical transformation的性質，變換座標後積分完會一樣)

從這個說明可以先知道一件事情：若想要求得一個系統的演化，就變換回initial coordinate $(q_0, p_0, t_0)$，一切就都會很清楚。

Note:
Canonical Transformation $$ (q,p,H)\to(Q,P,K) $$

例子：從初始條件看，$K=0$沒有Dynamics

按照前面的說明，我們現在進一步來看，選定初始條件

\[t_0=\text{fixed},\quad dt=0\\ (q_0,p_0)=\text{known}\]

解法

從前面知道

\[p_fdq_f-H_fdt_f=p_0dq_0-H_0dt_0+dS^*\]

因為初始條件$dt=0$，所以

\[p_fdq_f-H_fdt_f=p_0dq_0-H_0\cdot 0+dS^*\]

等號右邊第二項，我們可以利用數學技巧改寫成以下，反正都是0

\[p_fdq_f-H_fdt_f=p_0dq_0-0\cdot d{t_f}+dS^*\]

這麼做有個好處，$K$(轉換後的$H$)就可以視為0了！

$K=0$的含意

記得

\[\frac{d\vec{Q}}{dt}=\frac{\partial K}{\partial \vec{P}}\\ \frac{d\vec{P}}{dt}=-\frac{\partial K}{\partial \vec{Q}}\]

若$K=0$，那就沒有dynamic啦！$(Q, P)$都不會隨著時間變動了，代表說當我們做canonical transformation，去map

\[(q_f,p_f,H_f)\to(Q,P,K)\\ (q_f,p_f,t_f)\to(q_0,p_0,t_0)\]

可知

\[Q=q_0=\text{constant }(\because K=0)\\ P=p_0=\text{constant }(\because K=0)\\ t_0=\text{all the same}\]

這說明了什麼？其實是一個很廢的結果，就是若有人問你一個系統的演化，你跟他回答：「我知道這個系統有一個不變量，叫做起始位置和速度」。

那不是必然嗎！我們例子最一開始的假設就是定你想要從哪裡出發了，初始條件本來就已知，初始條件不變，真的聽君一席話，還是一席話。


可是這裡想要表明的重點是，我們真的能用Canonical Transformation從initial的座標角度看了！

Hamiltonian-Jacobi Equation

但如果接續這個例子繼續看

\[p_fdq_f-H_fdt_f=p_0dq_0+dS^*\]

還是有一個問題，我們看起來還是必須知道真實軌跡$S^* $的functional form，才會知道$(q(t),p(t))$的系統動態演化。

而這時Hamiltonian-Jacobi Equation就來了，這個Equation告訴我們不用解軌跡了！


轉個方式想，我們不直接解真實軌跡，我們解另外一個問題。


因為$S^* $會滿足特定的PDE(partial differential equation)，所以我們不用真的去解$(q(t),p(t))$，只要解PDE，就能夠得到particle dynamics。

這個PDE就一樣是我們提過的

\[p_f=\frac{\partial S^*}{\partial q_f}\\ H_f=-\frac{\partial S^*}{\partial t_f}=-H\bigg|_{t_f}\]

加上我們知道functional form of $H(q,p,t)$

所以以上代進去就會知道

\[-\frac{\partial S^*}{\partial t_f}=H\left(q_f,\frac{\partial S^*}{\partial q_f},t_f\right)\]

一旦這個PDE解出來，就是屬於場論(field theory)，我們不用再去單獨追蹤和解一個粒子的軌跡，而是透過解出整個場的PDE，解完後，軌跡自然就知道了。

Note:
要注意，我們要解的PDE並沒有$(t_0,q_0)$的變數，代表這兩個是可以自由選擇的，所以解這個的PDF自由度無限大。

舉例來說，我們可以把這個當作是initial value problem for S。

首先找個已知的定

\[S(q,t=t_0)\equiv f(q)\]

代表已知

\[\frac{\partial S}{\partial q}=\frac{\partial f}{\partial q}\]

就能知道

\[H\left(q_f,\frac{\partial S}{\partial q_f},t_f\right)=-\frac{\partial S}{\partial t_f}\]

整理一下

  • $q$一開始已知，因為$\frac{\partial S}{\partial t_f}$知道，所以知道下一秒在$q$的$S$。
  • 也因為$\frac{\partial S}{\partial q}$知道，所以也會知道下一秒在隔壁$q’$的$S$。
  • 結合就會知道速度$\frac{dS}{dt}$。
  • 繼續這樣推，空間中每個$S$都能知道，下一個瞬間的$S$也都可以算出來。
  • 整個軌跡就都能求出來了，所以主要就是看一開始的$f(q)$怎麼取。

所以為了避免自由度無限大的事情，你可以自己限制在某N個DOF，去加一些調整的變數

\[S=S(q,t,\vec{c}),\quad\vec{c}=\text{N tunable paramter}\]

例子

舉一維例子，我們知道

\[H=\frac{p^2}{2m}+V(q)\]

套用Hamiltonian-Jacobi Equation

\[-\frac{\partial S^*}{\partial t_f}=H\left(q_f,\frac{\partial S^*}{\partial q_f},t_f\right)\]

代進去得

\[\frac{1}{2m}\left(\frac{\partial S}{\partial q}\right)^2+V(q)=-\frac{\partial S}{\partial t}\]

接著用分離變數法，把$q,t$分開。


定

\[S\equiv w_0(t)+w(q)\]

所以

\[\frac{1}{2m}\left(\frac{dw}{dq}\right)^2+V(q)=-\frac{dw_0}{dt}\equiv E\]

($E$常數其實就是$\frac{\partial S}{\partial t}$，就是total energy的物理量。)

簡單積分移項

\[w_0=-E(t-t_0)\\ w=\pm\int_{-q}^{q}\sqrt{2m(E-V(q))}dq\]

得

\[S=\pm\int_{q_0}^{q}\sqrt{2m(E-V(q))}dq-E(t-t_0)\]

不過這還不是真實軌跡$S^*$，因為$E$還沒定好。

這邊直接來個物理直覺猜測吧，就設(我們簡單取正號)

\[S^*\equiv S\left(E=\frac{p_0^2}{2m}+V(q_0)\right)\]

代回去驗證看看

(小小note一下，這裡對$q_0$微分，$q_0$是變數，所以萊布尼茲規則需要對這個是變數的下限做處理，而在物理理解上，初始條件的位置也被視為可變的，要研究對初始條件的敏感性，所以等號右邊的第一項，正是萊布尼茲規則對下限變數處理的結果)

\[-p_0=\frac{\partial S^*}{\partial q_0}\\ -p_0=-\sqrt{2m(E-V(q_0))}+\int_{q_0}^{q}\frac{\partial}{\partial E}\sqrt{2m(E-V(q))}\frac{\partial E}{\partial q_0}dq-(t-t_0)\frac{\partial E}{\partial q_0}\]

等號左邊和等號右邊第一項相等，可以消掉

\[\frac{\partial E}{\partial q_0}\left(-(t-t_0)+\int_{q_0}^{q}\sqrt{2m}\frac{\frac{1}{2}}{\sqrt{E-V(q)}}dq\right)=0\\ \Rightarrow\left(-(t-t_0)+\int_{q_0}^{q}\sqrt{2m}\frac{\frac{1}{2}}{\sqrt{E-V(q)}}dq\right)=0\\ \Rightarrow t-t_0=\int_{q_0}^{q}\sqrt{2m}\frac{\frac{1}{2}}{\sqrt{E-V(q)}}dq=\int_{q_0}^{q}\frac{m}{\sqrt{2m(E-V(q))}}dq=\int_{q_0}^{q}\frac{m}{p}dq\]

看看我們得到什麼了！

\[t-t_0=\int_{q_0}^{q}\frac{1}{v}dq\\ (\frac{dq}{dt}=v, \quad\frac{dq}{v}=\Delta t)\]

完全正確的time dependece！

小結

Hamiltonian-Jacobi Equation 是 PDE，有無限多種DOF(solution)，但我們在一維的情況下，用分離變數找到一個常數(tunable parameter)，再用物理直覺猜測其為能量，代進去算也確認無誤。

You may also enjoy