Cjue25

Good things take time

最後，我們來延伸一下，看量子力學裡面的波函數。

因為記得前面講到的，Hamitonian-Jacobi Equation其實已經不管軌跡的概念，用到的是場論，而量力的波函數也是場方程式，所以也可以運用到這類的例子。

Schrödinger Equation

知道薛丁格方程式

\[H(\vec{q},\vec{p})\psi=i\hbar\frac{\partial \psi}{\partial t},\quad\text{linear in }\psi\\ \vec{p}\equiv \frac{\hbar}{i}\nabla=\frac{\hbar}{i}\frac{\partial}{\partial \vec{q}}\]

例子：Short Wave Length Limit

波函數

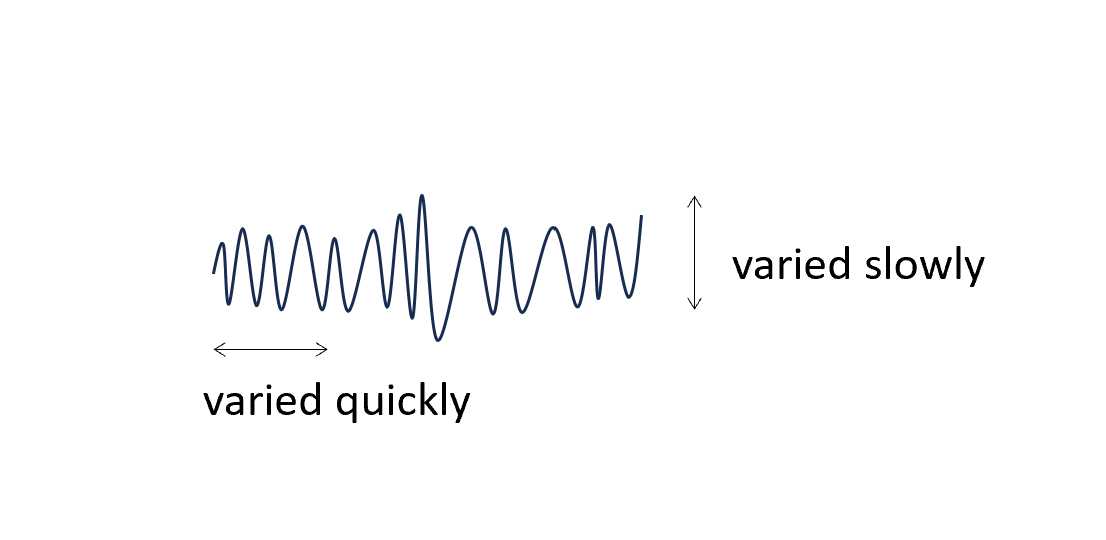
\[\psi\equiv Ae^{i\frac{S}{\hbar}}\]

這裡short wave lenght limit的意思是指，當振福$A$隨著時間演化的時候，或變化位置的時候，相較於phase$\frac{S}{\hbar}$的變化，$A$變得很慢。

接著，我們將$p$作用到$\psi$，但做一些近似

\[\begin{align*} \vec{p}\psi&=\frac{\hbar}{i}\nabla\left(Ae^{i\frac{S}{\hbar}}\right)\\ &\approx \frac{\hbar}{i}A\nabla\left(e^{i\frac{S}{\hbar}}\right)\\&\quad(\nabla A\text{ is small, ignore the spatial change of }A)\\ &=\frac{\hbar}{i} A\left(\frac{i}{\hbar}\nabla S\right)e^{i\frac{S}{\hbar}}\\ &=\psi\nabla S \end{align*}\]

再一次

\[\begin{align*} \vec{p}^2\psi&=\vec{p}\cdot(\vec{p}\psi)\\ &=\vec{p}\cdot\psi(\nabla S)\\ &=\frac{\hbar}{i}\nabla\cdot[\psi(\nabla S)]\\ &\approx (\nabla S)\cdot\left(\frac{\hbar}{i}\nabla \psi\right)\\ \\&\quad(\nabla\cdot\nabla S\text{ is small})\\ &\approx\nabla S\cdot(\psi\nabla S)\\ &\approx\psi(\nabla S)^2 \end{align*}\]

又Hamiltonian Operator

\[\hat{H}=\frac{p^2}{2m}+V(\vec{q})\]

所以最後可得

\[\hat{H}(\vec{q},\vec{p})\psi\approx\psi(H(q,\nabla S)),\quad(\nabla S = \vec{p})\]

一樣地，算右邊

\[\begin{align*} i\hbar\frac{\partial \psi}{\partial t}&=i\hbar\frac{\partial}{\partial t}\left(Ae^{i\frac{S}{\hbar}}\right)\\ &\approx i\hbar A\frac{\partial}{\partial t}\left(e^{i\frac{S}{\hbar}}\right)\\ &=i\hbar A\frac{i}{\hbar}e^{i\frac{S}{\hbar}}\frac{\partial S}{\partial t}\\ &=-\psi\frac{\partial S}{\partial t} \end{align*}\]

整合

\[H(\vec{q},\vec{p})\psi=i\hbar\frac{\partial \psi}{\partial t}\\ \Rightarrow \psi(H(q,\nabla S))=-\psi\frac{\partial S}{\partial t}\\ \Rightarrow H(q,\nabla S)=-\frac{\partial S}{\partial t}\]

這不就是Hamiltonian-Jacobi Equation嗎！

Hamiotonian-Jacobi 古典力學登峰之作

H-J站在中間地帶，連結了Quantum & Classical。

可以將H-J視作wave phenomena和classical concept的連結橋梁，因為變分中我們一直在計算的action

\[S\equiv \int pdq-Hdt\]

可以被視作為兩個概念：

  1. “phase” of the wave propagating in space time
  2. certain information carried by “calssical trajectories”

條列一下這個想法的重點：

  • 從純粹的量力出發，$\psi= Ae^{i\frac{S}{\hbar}}$，近似後的phase $S$和H-J的$S$相等！
  • 可以繼續求更高階，算出振福$A$隨時間和空間的變化(by S from H-J)。
  • 量力短波常近似可以看到，phase function的S滿足H-J的S，但H-J的S是從classical particle trajectory來的，代表量力中所謂的“機率” 場論(field information)，就是從古典的“particle trajetory” 來的！ (OMG)
  • 在解薛丁格波動方程的時候，隨時空變化很快的是phase S，S可以透過直接解來得到，但也可以藉由放一堆粒子，走古典軌跡，每個particle都算其$S^* =\int pdq-Hdt$，一堆$S^* $的所有資訊結合，就是true phase function的近似結果。 (軌跡資訊的結合得到波動的相位)
  • 我們表面是在解波動，沒有粒子沒有軌跡，都是機率，但這個重點是機率是哪來的？就是classicle particle造給你的！
  • 可以舉光學透鏡的例子，我們知道當光線平行射進凸透鏡，會折射集中到焦點，這個折射光線，就是particle trajectory。

(變分這堂課講了好幾個古典和量力之間的結合，每次看都覺得是件很神奇的事情！)

You may also enjoy