(6) 軌道 Hooke ─ 從 3D 看 2D 軌道
2D 看 1D SHO
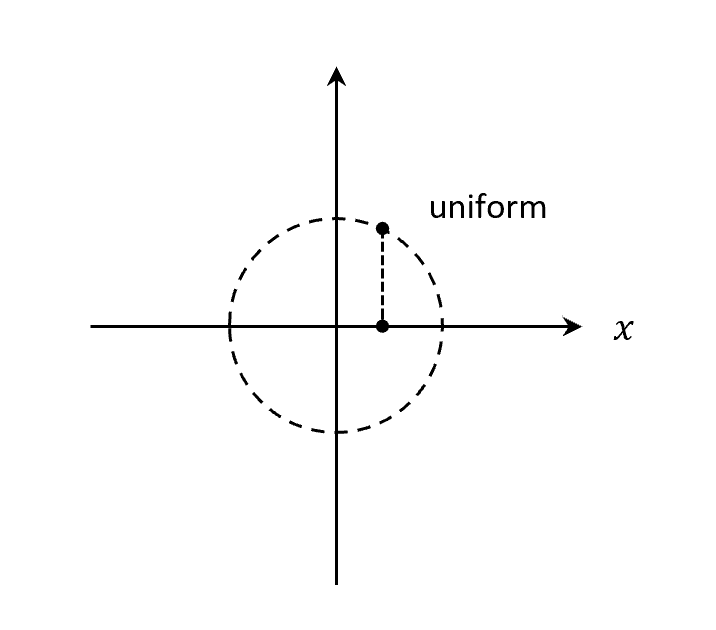
以前學過雖然 1D SHO 是在$x$軸上運動,但可以看成 2D 等速圓周運動的投影,代表可以用2D看1D。
1D SHM can be viewed as the orthogonal projection of some uniform circular motion
3D 看 2D 軌道
同理,我們現在也可以用 3D 看 2D Hooke’s 軌道。
限制在 3D 球面運動
現考慮2D運動
\[\begin{cases} \frac{d^2x}{dt^2} = -\omega^2x \\ \frac{d^2y}{dt^2} = -\omega^2y \end{cases}\]我們可以想像是一個 “free particle” 被限制在一個 sphere
\[F(x,y,z) \equiv \frac{x^2+y^2+z^2}{2} - \frac{R^2}{2}\]接著來套用之前變分第十五節的Lagragian Multiplier限制條件。
套用 Lagragian Multiplier
來算 Lagrangian (不管 mass, 沒有 V)
\[L = \frac{1}{2}(\dot{x}^2 + \dot{y}^2 + \dot{z}^2)\text{ constrain on }F(x,y,z)=0\]加入 multiplier
\[\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right) = \frac{\partial L}{\partial x} - \lambda(t) \frac{\partial F}{\partial x} = -\lambda(t) \frac{\partial F}{\partial x}\\ \Rightarrow \frac{d}{dt}(\dot{x}) = -\lambda(t)x\]同理,其他方向得
\[\begin{cases} \frac{d}{dt}(\dot{x}) = -\lambda(t)x \\ \frac{d}{dt}(\dot{y}) = -\lambda(t)y \\ \frac{d}{dt}(\dot{z}) = -\lambda(t)z \end{cases}\]我們想要對應前面 2D 的$\omega^2$,但是這裡的$\lambda(t)$還沒完整,要對應的話需要先證明$\lambda(t)$不是t的函式。
驗證 Holonomic Constraint
我們順便來看一下限制條件是不是 Holonomic,所以來算用變分第十四節來算算看是否滿足
\[\vec{f}\cdot(\nabla\times\vec{f})=0\]我們的條件,來算
\[\vec{f} = \nabla F = (x, y, z)\] \[\nabla \times \vec{f} = (\frac{\partial z}{\partial y} - \frac{\partial y}{\partial z}, \frac{\partial x}{\partial z} - \frac{\partial z}{\partial x}, \frac{\partial y}{\partial x} - \frac{\partial x}{\partial y})\\ = (0 - 0, 0 - 0, 0 - 0) = (0, 0, 0)\]因此
\[\vec{f} \cdot (\nabla \times \vec{f}) = (x, y, z) \cdot (0, 0, 0) = 0\]結果滿足Holonomic Constraints。
驗證能量守恆
能量也維持守恆
\[\frac{\dot{x}^2+\dot{y}^2+\dot{z}^2}{2}=E=\text{constant}\]來確認一下,用能量的寫法代入 Lagragian Multiplier 的公式,左右兩邊都乘上速度後相加
\[\begin{align} \frac{dE}{dt}&=0\\ &=\frac{d}{dt}\left(\frac{1}{2}( \dot{x}^2 + \dot{y}^2 + \dot{z}^2)\right)\\ &= -\lambda (x\dot{x} + y\dot{y} + z\dot{z})\\ &= -\frac{\lambda}{2} \frac{d}{dt} (x^2 + y^2 + z^2)\\ &= 0 \end{align}\]看起來是對的,因為
\[F(x,y,z) = 0, \quad\frac{x^2 + y^2 + z^2}{2} = \frac{R^2}{2}\]self-consistent。
證明 Multiplier 和時間無關
一樣Lagragian Multiplier 的公式,左右兩邊都乘上位置後相加
\[\begin{align} RHS &= -\lambda(t) \cdot (x^2 + y^2 + z^2)\\ &= -\lambda(t) R^2\\ LHS &= x \frac{d\dot{x}}{dt} + y \frac{d\dot{y}}{dt} + z \frac{d\dot{z}}{dt}\\ &= \frac{d}{dt} (x\dot{x} + y\dot{y} + z\dot{z}) - \left(\frac{dx}{dt} \dot{x} + \frac{dy}{dt} \dot{y} + \frac{dz}{dt} \dot{z}\right)\\ &= \frac{1}{2} \left(\frac{d}{dt} (x^2 + y^2 + z^2)\right)-\left(\frac{dx}{dt} \dot{x} + \frac{dy}{dt} \dot{y} + \frac{dz}{dt} \dot{z}\right)\\ &= 0 - (x^2 + y^2 + z^2) \\ &= -2E \end{align}\]左右整合
\[\Rightarrow \lambda(t) = \frac{2E}{R^2} = \frac{v^2}{R^2} = \text{constant}\\ (2E = \dot{x}^2 + \dot{y}^2 + \dot{z}^2 = \vec{v}^2 ,\quad \vec{v} = \text{ velocity on the spherical surface})\]對應 3D 球面等速直線運動
現在我們是算 free particle,唯一的限制是在球面上。並且在球面上路線不會轉彎,也就是不會有額外的切面力作用。
唯一的在球面上的限制,只有球面垂直的力,所以 free particle 會做的是「在曲面上等速直線運動」,也就是走大圓(great circle),所以看$\vec{v}$是 uniform,速度不會隨著時間而變!
因此$\omega$可以視為 angular speed on the spherical surface!
\[\omega^2=\lambda=\frac{v^2}{R^2}\\\]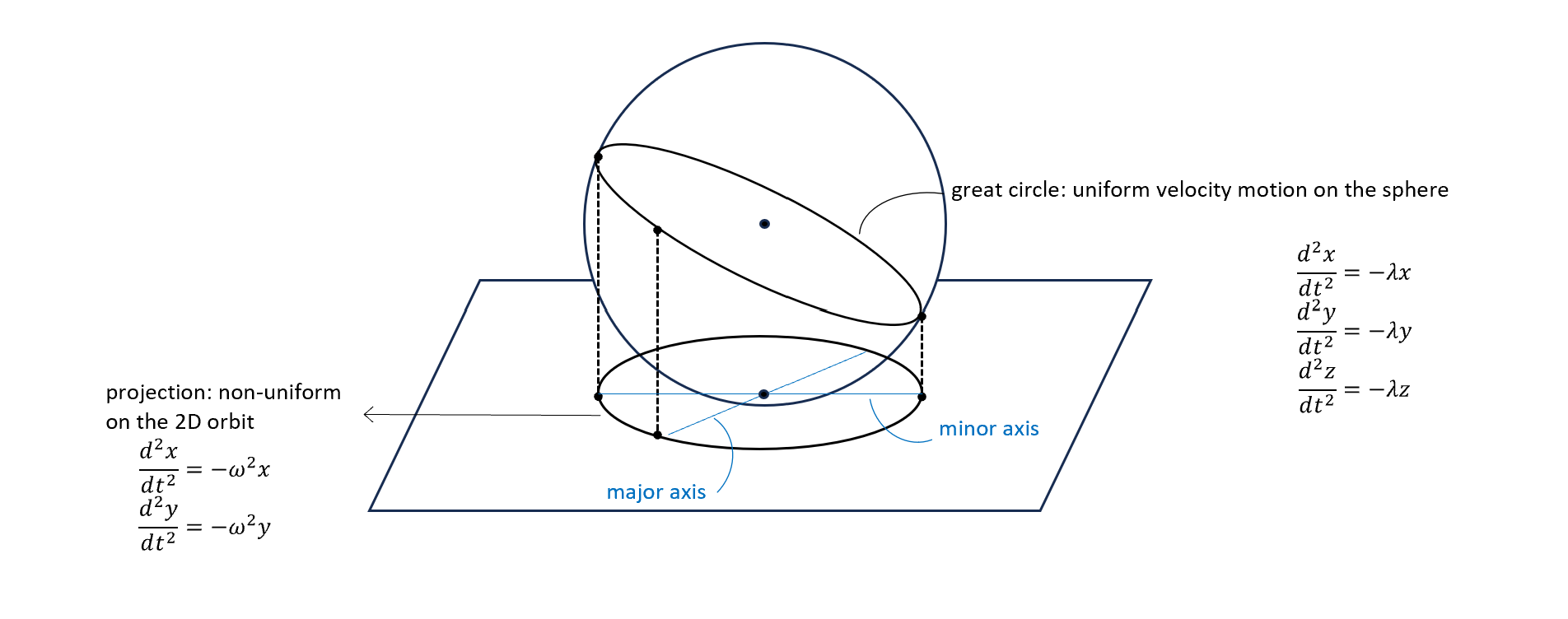
(可以對照變分第二十節)
對稱性與守恆量
2D SHO
能量
\[\frac{\dot{x}^2}{2}+\frac{\omega^2}{2}x^2=E_1\text{ conserved}\\ \frac{\dot{y}^2}{2}+\frac{\omega^2}{2}y^2=E_2\text{ conserved}\]將兩個decoupled oscillators視為整個系統,有著轉動對稱性,對應角動量守恆
\[x\dot{y}-y\dot{x}=L\text{ conserved}\]所以在原本 2D SHO 裡,有三個守恆量
\[E_{1_\text{(2D)}}, E_{2_\text{(2D)}} , L_{\text{(2D)}}\]3D System
一樣能量守恆
\[\frac{\dot{x}^2}{2}+\frac{\dot{y}^2}{2}+\frac{\dot{z}^2}{2}=E\text{ conserved}\](這可以從Lagragian不是時間的函式知道($\frac{\partial L}{\partial t} = 0$),有time-translation symmetry)
在球上運動,有旋轉對稱性,所以角動量守恆
\[\begin{cases} x\dot{y}-y\dot{x}=L_3\text{ conserved}\\ y\dot{z}-z\dot{y}=L_1\text{ conserved}\\ z\dot{x}-x\dot{z}=L_2\text{ conserved}\\ \end{cases}\]所以在 3D 系統裡,有四個守恆量
\[E_{\text{(3D)}}, L_{1_\text{(3D)}}, L_{2_\text{(3D)}} , L_{3_\text{(3D)}}\]2D vs 3D 守恆量對應關係
現在我們把2D和3D運動對在一起
\[L_{\text{(2D)}} \Leftrightarrow L_{3_\text{(3D)}}\]但還有其他問題
- \(L_{1_\text{(3D)}}, L_{2_\text{(3D)}}\)對應什麼?
- 3D 中的 $z, \dot{z}$的運動代表什麼?
- 3D看到的這些對稱性,反過來對應到實際的2D代表什麼?
- 是不是彼此組合後會可以有對應的關係呢?
簡短來說,我們的問題現在是:
Can we somehow “recover” the obvious \(L_{1_\text{(3D)}}=y\dot{z}-z\dot{y}\) using only variables that are available to the 2D oscillator? That is, expressing \(L_{1_\text{(3D)}}\) in terms of \(E_{1_\text{(2D)}}, E_{2_\text{(2D)}} , L_{\text{(2D)}}\)?
2D $\to$ 3D
平方一下,想說可能會有跟能量有關的項
\[L_{1_\text{(3D)}}^2 = (y\dot{z} - z\dot{y})^2 = y^2\dot{z}^2 + z^2\dot{y}^2 - 2y\dot{y}z\dot{z}\]另外知道
\[x^2 + y^2 + z^2 = R^2\\ x\dot{x} + y\dot{y} + z\dot{z} = 0\\ \dot{x}^2 + \dot{y}^2 + \dot{z}^2 = \omega^2 R^2 = 2E_{\text{(3D)}}\]所以
\[\begin{align} L_{1_\text{(3D)}}^2 &= {y}^2 (2E_{\text{(3D)}} - \dot{x}^2 - \dot{y}^2) + ( R^2 - x^2 -{y}^2) \dot{y}^2 - 2y\dot{y} ( -x\dot{x} - y\dot{y})\\ &= 2E_{\text{(3D)}} y^2 - y^2 \dot{x}^2 + R^2 \dot{y}^2 - {x}^2 \dot{y}^2 + 2 x\dot{x}y\dot{y}\\ &\quad(\because x\dot{y} - y\dot{x} = L_{\text{(2D)}}, \quad L_{\text{(2D)}}^2 = \dot{x}^2 \dot{y}^2 + \dot{y}^2 x^2 - 2x\dot{x}y\dot{y})\\ &=2E_{\text{(3D)}}y^2-y^2\dot{x}^2+R^2\dot{y}^2-x^2\dot{y}^2+x^2\dot{y}^2+y^2\dot{x}^2-L_{\text{(2D)}}^2\\ &=2E_{\text{(3D)}}y^2+R^2\dot{y}^2-L_{\text{(2D)}}^2\\ &=\omega^2R^2y^2+R^2\dot{y}^2-L_{\text{(2D)}}^2\\ &=R^2(\omega^2 y^2+\dot{y}^2)-L_{\text{(2D)}}^2\\ &=R^2\cdot 2E_{2_\text{(2D)}}-L_{\text{(2D)}}^2 \end{align}\]可以看到\(L_{1_\text{(3D)}}\) 用\(R, E_{2_\text{(2D)}},L_{\text{(2D)}}\)來表示了!
代表可以用 2D 的運動可以用來建構 3D 的旋轉對稱性。
3D $\to$ 2D
上面移項一下,我們也可以反過來用 3D 表達 2D,這裡可以看到一個系統的守恆量建構出另外一個系統的守恆量,或是說一個系統的時間對稱性,可以對應到另一個系統的旋轉對稱性。
\[\begin{cases} L_{\text{(2D)}}\equiv L_{3_\text{(3D)}}\\ E_{2_\text{(2D)}}=\frac{L_{1_\text{(3D)}}^2+L_{3_\text{(3D)}}^2}{2R^2}\\ E_{1_\text{(2D)}}=\frac{L_{2_\text{(3D)}}^2+L_{3_\text{(3D)}}^2}{2R^2}\\ \end{cases}\]但是 3D 有四個守恆量,那多一個是什麼 Redundant Quantity?
跟上面同理,其實我們可以額外算 $E_{3}$
\[E_{3}=\frac{L_{1_\text{(3D)}}^2+L_{2_\text{(3D)}^2}}{2R^2}\\ E_1+E_2+E_3=E_{\text{(3D)}}\]代表其實只要有\(L_{1_\text{(3D)}}, L_{2_\text{(3D)}} , L_{3_\text{(3D)}}\)就可以了,3D下仍然是三個守恆量,能量那項可以透過其他項組合出來。
這邊要注意的是,雖然不同守恆量是對應不同的對稱性,但並不代表守恆量彼此會是獨立的,就像我們可以用$L$去建構$E$。
小結
這邊再放一次這張圖,總結來說,對於Hooke的 2D 軌道,我們可以從 3D 的球面直線運動往下投影得到。

